Упражнения

1. Покажите, что формулы преобразования (4) не изменяют расстояния до начала координат.

2. Покажите, что расстояние между  двумя точками, полярные координаты которых (ρ₁, φ₁) и (ρ₂, φ₂), определяется по формуле

S = √{ρ₁² + ρ₂² − 2ρ₁ρ₂cos(φ₁ − φ₂)}.

1.8. «Недекартовые» системы координат в пространстве

Для задания положения точки в пространстве необходимо задать три числа-координаты, причем далеко не всегда декартовая система координат является наиболее удобной. Поэтому в геометрии трех измерений используются и другие системы координат. Познакомимся со своеобразным «гибридом»: полярную систему координат на плоскости дополним третьей координатой − расстоянием до плоскости. Такая система координат называется цилиндрической.

В этой системе координатами произвольной точки А являются (рис. 11):

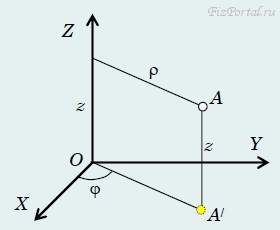
рис. 11

а) ρ − полярное расстояние, расстояние от точки до полярной оси (в качестве которой в данном случае выступает ось Z декартовой системы координат) либо, что равносильно, расстояние от проекции точки А на плоскость XOY (точка А^/) до начала координат О;

б) φ − полярный угол, угол между направлением на точку А^/ и осью X;

в)  z − расстояние от точки до плоскости XOY.

Для наглядного представления системы координат часто изображают координатные поверхности, то есть множества точек, для которых одна из координат постоянна. Для декартовой системы координат такими поверхностями являются плоскости. Так, например, условию z = const удовлетворяют точки плоскости, параллельной XOY.

В отличие от  декартовых, цилиндрические координаты являются криволинейными − их координатные поверхности не являются плоскостями.

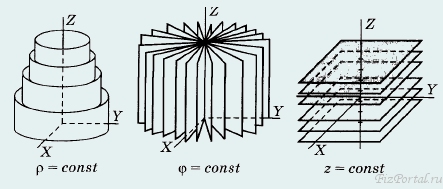
рис. 12

На рис. 12 изображены семейства координатных плоскостей для цилиндрической системы: − условию ρ = const удовлетворяют точки, лежащие на поверхности цилиндра радиуса ρ, коаксиального (соосного) с осью Z,

− поверхности постоянного полярного угла φ = const представляют собой полуплоскости, проходящие через ось Z;

− поверхности z = const по-прежнему плоскости перпендикулярные оси Z.

В заключение данного раздела заметим, что число различных криволинейных систем координат в пространстве трех измерений достаточно велико.

1.9. Существует ли четвертое измерение?

В научно-фантастических произведениях иногда встречаются сюжеты (рис. 13 −  автор Эшер), в которых разумные существа осваивают четвертое, пятое и так далее измерения¹. Повышение размерности пространства предоставляет новые, богатейшие возможности как для этих существ, так и для писателей-фантастов. Сравните двухмерную плоскость и трехмерное пространство! Для того чтобы «выйти» из плоскости в трехмерное пространство, можно предложить следующий метод: из центра окружности необходимо провести бесконечный луч, который нигде не пересекает окружность − такой луч лежит в третьем измерении. По аналогии можно предложить «путь в четвертое измерение»: из центра сферы необходимо провести луч, который нигде не пересекает сферу. Вообразили? Еще один способ: провести прямую, которая перпендикулярна трем взаимно перпендикулярным прямым. Конечно, если вам не удалось представить себе такой луч или такую прямую, то это еще не является доказательством отсутствия четвертого измерения в нашем пространстве.

рис. 13

Попытаемся представить, к каким наблюдаемым явлениям могло бы привести наличие дополнительного измерения. Например, из четвертого измерения можно было бы заглянуть внутрь любого трехмерного тела (как из третьего измерения можно видеть «внутренности» любой плоской фигуры). Далее, был бы возможен бесследный «уход» и обратное появление в любом другом месте любых материальных тел (опять же представьте себе, что будет происходить на плоскости, которую пересекает трехмерное тело). К настоящему времени таких фактов не зафиксировано. Более того, не известны такие явления, которые не могли бы быть объяснены с точки зрения пространства трех измерений.

Еще одним доказательством трехмерности пространства, в котором мы обитаем, является ряд физических законов. Рассмотрим, например, точечный источник, который посылает свет во все стороны равномерно. Понятно, что энергия, пересекающая поверхность любой сферы, внутри которой находится источник, должна быть постоянна. Следовательно, интенсивность света (то есть энергия, приходящаяся на единицу площади) должна убывать обратно пропорционально площади сферы, то есть обратно пропорционально квадрату расстояния. Если бы свет распространялся и в четвертом измерении, то его интенсивность убывала бы обратно пропорционально кубу расстояния. Эксперимент однозначно утверждает, что интенсивность убывает обратно пропорционально квадрату расстояния. Эти и другие факты утверждают, что наше пространство действительно трехмерно.

Таким образом, ответ на вопрос этого раздела, в настоящее время следующий: пространство четырех и более измерений является математической абстракцией. Можно изучать свойства геометрических объектов в таких пространствах при решении целого ряда задач, в том числе физических, бывает полезно их рассматривать в многомерных пространствах. Однако в настоящее время нет никаких оснований полагать о реальном существовании четвертого измерения в том смысле, что реально существуют некоторые материальные тела вне пространства трех измерений.