Упражнение

Покажите, что расстояние между двумя точками в пространстве вычисляется по формуле

s = √{(x₂ − x₁)² + (y₂ − y₁)² + (z₂ − z₁)²}.

Давайте теперь попытаемся вычислить расстояние между этими же точками, но в другой системе отсчета Х^/О^/Y^/, которая сдвинута относительно исходной системы координат ХОY. В этой системе отсчета координаты точек А₁ и А₂ можно найти по формулам преобразований (1)

x₁^/ = −x_o + x₁; x₂^/ = −x_o + x₂. (5)\

Как следует из этих формул, х₂ − х₁ = х₂^/ − х₁^/,

что, впрочем, и должно быть: если вторая точка лежит правее первой, то это их взаимное расположение не зависит от выбора системы координат, расстояние между проекциями точек на одну и ту же ось не зависит от начала отсчета. Аналогичное соотношение можно записать и для координат у этих точек, поэтому, как следует из здравого смысла, результат вычисления по формуле (4) не зависит от выбора системы координат (конечно, при неизменной единице измерения длины). Мы показали это для преобразования сдвига, однако очевидно, что и при повороте системы координат формула (4) должна давать один и тот же результат. Весьма интересная ситуация: все четыре координаты при изменении системы отсчета изменяются, а величина расстояния остается неизменной!

Величины, которые остаются неизменными при изменении системы координат, называются инвариантными.

Вот еще одно подтверждение возможности использования систем координат − можно найти физические величины, которые не зависят от выбора системы координат. Поиск таких инвариантных физических величин очень важен, потому что, как правило, именно они проще всего поддаются измерению, именно они фактически определяют протекание того или иного физического процесса, именно они убеждают скептиков в возможностях правильного физического описания различных явлений.

1.7. Полярная система координат

Декартовая система координат на плоскости является, безусловно, самой простой, однако не единственно возможной. Во многих случаях предпочтительнее использовать другие криволинейные системы координат. Среди этих координат наиболее часто используется полярная система (рис. 9).

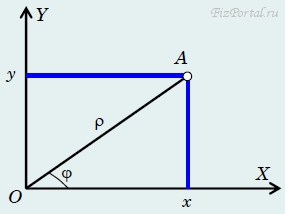
рис. 9

Положение точки А на плоскости в этом случае описывается координатами: величинами ρ − полярное расстояние (ОА) и φ − полярный угол (АОх). Очевидно, что координата ρ неотрицательна, угол φ может принимать любые значения. Легко выразить декартовые координаты точки через полярные:

x = ρcosφ; y = ρsinφ. (1)

Обратное преобразование несколько сложнее:

ρ = √{x² + y²}; φ = arctg(y/x) ± kπ. (2)

Заметим, что полярный угол определяется неоднозначно, при добавлении к нему любого кратного 2π положение точки на плоскости не изменяется. Эта неоднозначность редко приводит к недоразумениям, зато оговоренное произвольное (от минус до плюс бесконечности) изменение угла позволяет легко и красиво описывать некоторые виды механического движения тел (например, вращение).

Получим теперь формулы преобразования координат точки при повороте системы координат. Рассмотрим две декартовые системы координат ХОY и Х^/ОY^/, начала отсчета которых совпадают, а оси повернуты на некоторый угол φ_o (рис. 10).

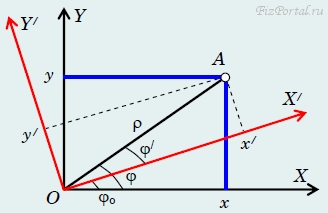
рис. 10

Очевидно, что в обеих системах расстояния до начала отсчета одинаковы, а полярные углы связаны линейным соотношением

ρ^/ = ρ, φ^/ = φ − φ_o. (3)

Эти простые формулы и выражают преобразования координат при повороте осей. Получим также и формулы преобразования поворота для декартовых координат. Запишем выражения для декартовых координат в «штрихованной» системе отсчета

x^/ = ρ^/cosφ^/ = ρcos(φ − φ_o);

y^/ = ρ^/sinφ^/ = ρsin(φ − φ_o).

Используем известные тригонометрические формулы для синуса и косинуса разности углов:

x^/ = ρcos(φ − φ_o) = ρcosφcosφ_o + ρsinφsinφ_o;

y^/ = ρsin(φ − φ_o) = ρsinφcosφ_o − ρcosφsinφ_o.

Наконец, замечая, что

ρcosφ = x, а ρsinφ = y,

получим искомые выражения:

x^/ = xcosφ_o + ysinφ_o; y^/ = ycosφ_o − xsinφ_o. (4)

Заметьте, что формулы обратного преобразования получаются из системы (4) посредством очевидной замены φ_o на −φ_o, что также является следствием относительности координат. Эти преобразования, конечно, можно было получить и геометрическим способом с помощью приведенного рисунка.