1.5. Преобразования координат

Рассмотрим, как будут изменяться координаты точек при различных преобразованиях системы отсчета. Первый пример − изменение единицы измерения длины при неизменных начале отсчета и направлениях осей координат. Так как координаты точки представляют собой расстояния от проекций точки на оси координат до начала отсчета, то при изменении единицы измерения длины координаты будут изменяться так же, как изменяется численное значение длин и расстояний, то есть умножаться на коэффициент, связывающий различные единицы измерения. При изменении направления оси очевидно, что соответствующие координаты изменят знак на противоположный.

Получим теперь формулы преобразования координат при  сдвиге начала отсчета. Пусть на плоскости введены две системы декартовых координат ХОY и Х^/О^/Y^/, оси которых попарно параллельны (рис. 7)

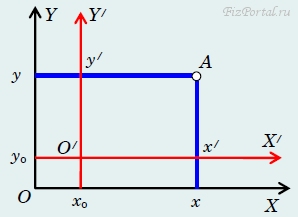
рис. 7

Обозначим координаты точки О^/ в системе отсчета ХОY через х_o и у_o. Пусть координаты произвольной точки А в системе отсчета Х^/О^/Y^/ равны х^/ и у^/. Тогда, как следует из рисунка, координаты х, у этой же точки в системе отсчета ХОУ могут быть найдены по формулам

x₁ = x_o + x^/; y₁ = y_o + y^/. (1)

Легко записать формулы  обратного перехода от координат в системе отсчета ХОY к координатам в системе отсчета Х^/О^/Y^/:

x^/ = −x_o + x; y^/ = −y_o + y. (2)

Как и следовало ожидать, формулы обратного  преобразования (2) полностью аналогичны формулам (1), так как −х_o и −у_o есть координаты точки О в системе отсчета Х^/О^/Y^/. Эти формулы называют преобразованиями сдвига. Назовем систему отсчета ХОY исходной, а систему отсчета Х^/О^/Y^/ смещенной. (Очевидно, что эти названия условны, так как две рассматриваемые системы равноправны, и их можно поменять местами.)

Тогда правила преобразований сдвига можно сформулировать следующим образом: при смещении начала координат координаты всех точек уменьшаются на величину соответствующего смещения начала отсчета; координата точки в смещенной системе координат равна координате в исходной системе минус соответствующая координата начала отсчета смещенной системы.

 Упражнение. Получите формулы преобразования сдвига для  одномерного и трехмерного случаев.

Существенным является тот факт, что в любом случае, при любом изменении  системы отсчета можно найти формулы преобразования координат. Следовательно, если положение тела описано в одной системе отсчета, то оно описано и в любой другой.

1.6. Расстояние между двумя точками

Если нам известны координаты точек (естественно, в заданной системе  координат), то однозначно известно их положение. Поэтому можно найти любые геометрические характеристики их взаимного расположения. Получим формулы, позволяющие по известным координатам двух точек вычислить расстояние между ними. В простейшем случае, когда две точки  А₁ и А₂ находятся на одной оси, расстояние между ними определяется формулой

s = |x₂ − x₁|, (3)

где х₁, х₂ − координаты точек А₁ и А₂ соответственно. Очевидно, что  расстояние от А₁ до А₂ равно расстоянию от А₂ до А₁, что и привело у к тому, что в формуле (3) появился знак модуля числа. Пусть на плоскости задана система  координат ХОY, в которой координаты точки А₁ равны х₁ и у₁, а координаты точки А₂, соответственно, равны х₂ и у₂ (рис. 8).

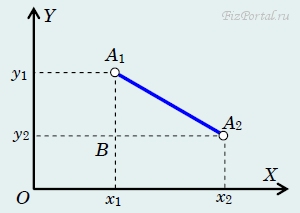
рис. 8

В прямоугольном треугольнике  А₁А₂В длина стороны А₂В равна |х₂ − х₁|, а длина стороны А₁В = |у₂ − у₁|, поэтому расстояние между точками А₁ и А₂ можно найти по теореме Пифагора:

s = √{(x₂ − x₁)² + (y₂ − y₁)²}. (4)