1.3. Координаты точки в пространстве

Положение точки в пространстве однозначно может быть определено с помощь  трех чисел − координат. Это утверждение является следствием того факта, что пространство, в котором мы живем, является трехмерным. После подробного  изучения декартовых координат на прямой и на плоскости построение системы пространственных координат легко провести по аналогии. Выберем произвольно точку О − начало отсчета, через которую проведем произвольно три взаимно перпендикулярные прямые − оси координат X, Y, Z. Зададим положительные направления осей и стандартным образом введем координаты точек на этих осях (назовем их х, y, z) (рис. 6).

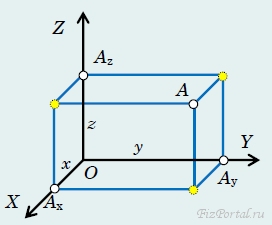
рис. 6

Декартовыми координатами произвольной точки  А в пространстве являются координаты х, y, z точек − проекций A_x, А_y, А_z на выбранные оси координат X, Y, X. Для того чтобы спроецировать точку А на ось X трехмерной системы координат, можно поступать различными способами: опустить перпендикуляр на плоскость ХОY, а затем спроецировать точку − основание этого перпендикуляра на ось X; можно и сразу опустить перпендикуляр из точки А на ось X. Еще один способ − построить прямоугольный параллелепипед с противоположными вершинами в точках А и О, ребра которого параллельны осям координат. Тогда длины этих ребер (с учетом знаков) будут являться координатами точки А. Числа −  координаты проекций − определяются стандартным образом: модуль числа равен расстоянию до начала отсчета, а знак определяет, с какой стороны от начала отсчета лежит данная точка. Таким образом, каждой точке пространства ставится в соответствие тройка чисел − х, y, z.

Естественно, декартовая система координат в пространстве не является единственно возможной, используются и другие системы координат.

1.4. Относительность координат

Итак, мы добились поставленной цели: дали «имя», указали «точный адрес» произвольной точке пространства − каждой точке пространства поставили в однозначное соответствие набор чисел − координат. Однако знание только этих чисел не дает возможности указать конкретную точку. Эти числа-координаты имеют смысл только тогда, когда указана (известна) система отсчета − начало отсчета, направление осей и единица измерения расстояний. Только в этом случае координаты указывают на конкретную точку пространства. Если изменить систему отсчета (начало отсчета, направление осей) или единицу измерения, то изменятся и координаты всех точек. Иными словами, координаты всех точек относительны, заданы относительно оговоренной системы координат. Выбор системы координат, как мы неоднократно подчеркивали, совершенно произволен. Существенна ли эта неопределенность в выборе системы координат? Нужно ли вообще говорить о координатах, если каждый имеет полное право ввести свою собственную систему координат? Мы вынуждены примириться с этим произволом и бояться его не надо, потому что:

− иного способа математического описания положения точки в пространстве не существует;

− всегда можно в каждом конкретном случае договориться о выборе системы отсчета, тем более что часто наиболее удачный выбор системы отсчета очевиден и определяется описываемой ситуацией. Например: расположение мебели в конкретной комнате не слишком удобно проводить в системе отсчета, связанной с почтамтом, скорее всего, каждый расположит начало отсчета в одном из углов комнаты и направит оси координат вдоль «ребер» комнаты;

− произвол в выборе системы отсчета дает нам определенную свободу, дает право воспользоваться возможностью выбора в своих интересах так, чтобы в каждом конкретном случае упростить описание физического явления;

− всегда можно (и следует) найти такие физические величины, которые не зависят от выбора системы координат. Например – расстояния между точками, углы между прямыми, площади фигур;

– всегда возможно установить формулы преобразования координат при переходе из одной системы отсчета в другую.

Как видим (и в этом мы сможем убедиться неоднократно в дальнейшем), физика − наука демократичная, она предоставляет каждому «свободу выбора», только надо уметь, и не бояться, ею пользоваться. В физике существует множество законов, но «все, что не запрещено, разрешено», различные точки зрения допустимы, но вполне примиримы друг с другом либо путем компромисса, либо путем установления общих «правил игры».

Наконец, следует помнить, что в физике существуют некие «абсолютные ценности», не зависящие от выбранной точки зрения.