14.3. Суперпозиция движений

Мы изучили несколько простейших моделей движения. Сейчас постараемся показать, как из этих простых движений можно «конструировать» более сложные и красивые движения. Слово «суперпозиция» обозначает сложение, наложение, сочетание, оно очень часто используется в физике.

Возможность такого наложения различных видов движения обусловлена возможностью описывать его в различных системах отсчета и переходить из одной системы в другую по формулам

Теперь мы можем независимо задавать закон движения в подвижной системе отсчета r^/(t), закон движения самой движущейся системы r_o(t) и получать более сложный закон движения. Далее может быть, что и неподвижная система отсчета движется относительно другой, еще более неподвижной системы. Тем самым добавляется еще одно слагаемое и т. д. На этом пути открываются практически неограниченные возможности. Рассмотреть их всех невозможно, поэтому мы вынуждены ограничиться несколькими простыми, но красивыми движениями.

Движение тела, брошенного под углом к горизонту, можно представить в виде суперпозиции равномерного движения вдоль горизонтальной оси и равноускоренного движения вдоль вертикальной оси. Такой «суперпозиции» можно придать наглядный смысл: пусть в вагоне равномерно и прямолинейно движущегося поезда вверх подброшен небольшой шарик. В системе отсчета, связанной с вагоном, шарик движется вдоль вертикальной прямой с постоянным ускорением свободного падения. А в системе отсчета, связанной с землей, движение шарика будет движением по описанной ранее параболе. Отметим также, что «разложение движения на составляющие» не является однозначным¹. Так, то же движение тела, брошенного под углом к горизонту, можно представить в виде «суммы» равномерного движения вдоль прямой, направленной под углом к горизонту, задаваемой вектором начальной скорости, и равноускоренного движения вдоль вертикальной прямой. Фактически эти разложения мы использовали ранее при описании этого движения.

Суперпозиция вращательного и поступательного движений. Пусть материальная точка А движется по прямому стержню с постоянной скоростью v, а стержень вращается вокруг оси с постоянной угловой скоростью ω. Совместим начало системы отсчета с осью вращения (рис. 79).

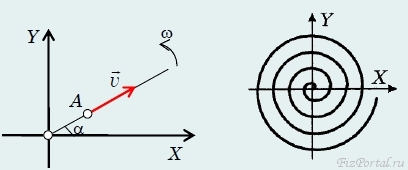
рис. 79

Тогда расстояние от точки А до начала отсчета и угол поворота стержня зависят от времени по законам

l = vt, α = ωt.

Зависимость декартовых координат точки от времени имеет вид

х = lcosα = vtcosωt;

х = lsinα = vtsinωt.

и описывает движение по спирали. Еще одна суперпозиция поступательного и вращательного движений. Пусть колесо радиуса R катится по горизонтальной поверхности без проскальзывания. Точка А расположена на расстоянии а от оси колеса (будем считать, что a может быть как меньше, так и больше R − такие точки можно найти, например, на железнодорожном колесе). Построим семейство траекторий точек колеса. Пусть в начальный момент времени центр колеса находится в точке О. Введем систему координат, ось X которой проходит вдоль поверхности, по которой катится колесо, а ось Y перпендикулярна этой поверхности и проходит через точку О (рис. 80).

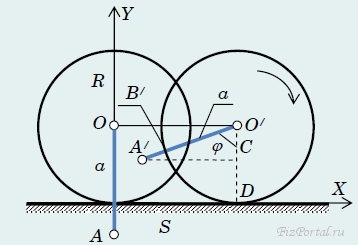
рис. 80

Выберем точку А на расстоянии а от центра и первоначально находящуюся на оси У. Посмотрим, как изменится положение этой точки, когда колесо повернется на некоторый угол φ = ωt (на рисунке это ∠A^/O^/D). Центр колеса сместится на расстояние S и займет положение О^/, а точка А окажется в точке А^/. Так как движение происходит без проскальзывания, то смещение колеса S = |OO^/| = |BD| будет равно длине дуги DB^/. Поэтому S = Rφ, где угол φ, естественно, измеряется в радианах. Координаты центра колеса будут равны

х_O' = S = Rφ, у_O' = R.

Рассматривая треугольник О^/А^/С, легко найти координаты рассматриваемой точки А^/:

Посмотрите на эти траектории (рис. 81) при а, изменяющемся от −3R до 3R (с шагом R/4). Не правда ли, эффектные кривые?!

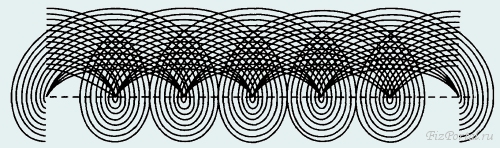
рис. 81

Суперпозиция двух вращательных движений. Посмотрим, какую траекторию описывает точка М колеса радиусом r, катящегося без скольжения по другой неподвижной окружности радиуса R (рис. 82).

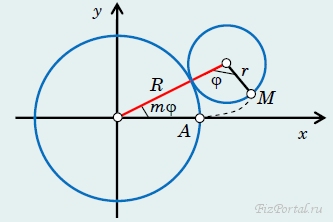
рис. 82

Обозначим φ = ωt − угол поворота колеса, m = r/R − отношение радиусов колеса и неподвижной окружности. Пусть А − начальное положение рассматриваемой точки. Из геометрических соображений можно получить параметрическое уравнение траектории точки М:

Вид траектории полностью определяется параметром m. Если этот параметр является рациональным числом m = p/q, (р, q − целые числа), то траектория является замкнутой.

Посмотрите на различные траектории, описываемые этими  уравнениями (рис. 83). На всех рисунках − в центре изображение окружности, по которой катится колесо.

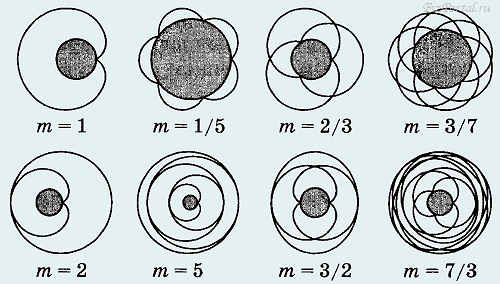
рис. 83

¹Дискуссия о том, какое разложение является «правильным», равносильна спору о том, какое разложение «7 = 5 + 2» или «7 = 3 + 4» точнее описывает свойства «семерки».