13.2. Равномерно движущаяся система отсчета

Пусть система Х^/О^/Y^/ движется относительно системы ХОУ с постоянной скоростью v. В любой момент времени соотношения между координатами выражаются соотношениями (1) − (2). В случае движущейся системы координат мы не можем логически строго утверждать, что течение времени будет таким же, как и в неподвижной системе. Вопрос о том, изменится ли ход часов, если они будут двигаться с постоянной скоростью, не может быть разрешен путем логических рассуждений. Ответ на него может дать только эксперимент, только опыт. Мы еще не раз будем возвращаться к этой проблеме, пока же примем как аксиому, подтвержденную многовековым опытом человечества, что течение времени одинаково в различных системах отсчета, движущихся друг относительно друга с постоянной скоростью.

Найдем соотношение между скоростями точки в подвижной¹ Х^/О^/Y^/ и неподвижной ХОУ системах координат. Опять воспользуемся соотношением (2) для вычисления скорости в неподвижной системе отсчета:

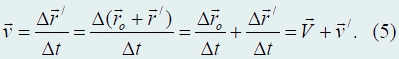
Легко заметить, что Δro/Δt = V − скорость движения подвижной системы, а Δr//Δt = v^/ − скорость точки относительно подвижной системы координат. Довольно часто применяется следующая терминология: скорость точки относительно подвижной системы координат v^/ называют относительной скоростью; скорость точки относительно неподвижной системы координат называют абсолютной скоростью; скорость одной системы координат относительно другой называют переносной скоростью. Используя эти названия, очень важное соотношение (5) можно словесно сформулировать так: абсолютная скорость точки равна сумме ее относительной скорости и переносной. Из соотношения (5) можно выразить относительную скорость:

Относительная скорость точки равна разности между ее абсолютной скоростью и переносной. Заметьте, что соотношению (6) можно дать и другое истолкование. Будем считать систему отсчета Х^/О^/Y^/ неподвижной, а систему ХОУ подвижной. Тогда переносная скорость (то есть скорость системы ХОУ относительно Х^/О^/Y^/) будет равна − V , поэтому соотношение (6) просто совпадает с формулой (5). Соотношения между скоростями (5) − (6) выполняются в любой момент времени, поэтому их можно использовать для того, чтобы установить связь между ускорениями точек в различных системах координат. Пусть точка А движется с ускорением а^/ относительно подвижной системы координат (будем по-прежнему считать, что переносная скорость является постоянной), тогда ее ускорение в неподвижной системе можно вычислить по следующим формулам:

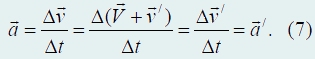
Мы доказали, что если одна система движется относительно другой с постоянной скоростью, то ускорения тел относительно этих систем отсчета одинаковы. Иными словами, ускорение является инвариантной величиной при переходе из одной системы отсчета в другую. Наше изложение можно продолжить в том же духе − рассмотреть случай ускоренного движения одной системы относительно другой. Сейчас мы не будем заниматься этим, так как при изучении динамики увидим, что системы, движущиеся друг относительно друга равномерно и прямолинейно, занимают особое место в механике, именно им уделяется особое внимание, на что есть весьма серьезные физические причины.

¹Очередной раз отметим условность названий систем отсчета: если одна система движется относительно другой, то справедливо и обратное − выбор неподвижной и движущейся систем остается за исследователем.