1.2. Координаты точки на плоскости

Положение точки на плоскости нельзя задать с помощью одного числа, так как  нельзя провести линию, проходящую через все точки плоскости. Положение точки на плоскости (и на любой другой заданной поверхности), как мы сейчас это покажем, можно описать с помощью двух чисел (двух координат). Поэтому говорят, что заданная поверхность имеет два измерения, а движение по поверхности является двумерным. Рассмотрим один из способов описания положения точки на плоскости (способ указания «адреса» точки) − декартовую систему координат. Для этого выберем на заданной плоскости произвольную точку О, которую назовем началом отсчета, и проведем через нее две произвольные взаимно перпендикулярные прямые − оси координат. Выберем положительные направления этих осей и зададим на них координаты, так как мы это сделали в случае одной оси. Совместим начала отсчетов на этих прямых с их точкой пересечения. Обозначим координаты точек на одной прямой х, а на другой у (рис. 4).

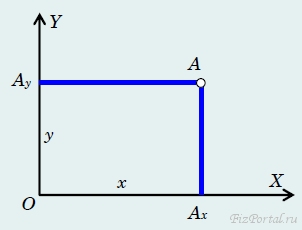
рис. 4

Координаты произвольной точки  А на плоскости определим следующим образом: − опустим перпендикуляры из точки А на ось ОХ (основание перпендикуляра − точка Ах) и на ось ОY (точка А_у), (говорят также: спроецируем точку на оси координат − точка А_х есть проекция точки А на ось ОХ; точка А − проекция точки А на ось ОY); − координаты х, у точек проекций и А_у являются координатами точки А. Этой паре чисел  х, у можно дать и несколько иное толкование (не противоречащее данному выше): модуль координаты х равен расстоянию до оси Y, а знак указывает, с какой стороны от оси лежит данная точка (аналогично для координаты у). Начало отсчета и  оцифрованные оси координат (то есть задана единица измерения расстояния) называются системой отсчета. Если начало отсчета «привязано» к какому-нибудь конкретному телу, то часто его называют телом отсчета. Прекрасной и хорошо  знакомой иллюстрацией декартовой системы координат на плоскости служит тетрадный лист в клеточку, если на нем провести две перпендикулярные прямые линии − оси координат. В принципе, можно с помощью двух чисел задать положение  произвольной точки на любой заданной известной поверхности (а не только плоскости). Однако это сделать сложнее, чем определить координату на произвольной линии. Поэтому мы ограничимся известным примером − географические широта и долгота являются координатами точки на поверхности земного шара, так как они однозначно определяют положение точки (рис. 5).

рис. 5

В общем случае задание координат на произвольной поверхности равносильно нанесению на поверхность некоторой координатной сетки − набора линий, которые можно построить следующим образом: зафиксируем одну из координат, а вторую будем изменять во всей области допустимых значений. Тогда множество точек поверхности, для которых одна из координат задана, представляет собой линию, которая называется координатной. Два семейства координатных линий и задают координатную сетку. Например, на глобусе набор параллелей и меридианов является координатной сеткой. Отметим, что построенная декартовая система координат не является единственно возможной. Достаточно широко в физике используются и другие (криволинейные) системы координат, например, полярная, с которой мы познакомимся несколько позже.