8.1. Вычисление мгновенной скорости и ускорения по известному закону движения

В предыдущих параграфах мы занимались решением основной задачи механики − искали закон движения материальной точки. Покажем теперь, как, зная закон движения, рассчитать кинематические характеристики движения − мгновенную скорость и ускорение.

Пусть закон движения имеет вид функции¹ x(t). Тогда мгновенную скорость можно вычислить по ее определению:

v(t) = Δx/Δt = (x(t + Δt) − x(t))/Δt.

При этом следует учесть, что величина Δt должна быть малой. Покажем использование этого метода для случая равноускоренного движения, при котором x(t) = x_o + v_ot + at²/2:

v(t) = (x(t + Δt) − x(t))/Δt = {(x_o + v_o(t + Δt) + a(t + Δt)²/2) − (x_o + v_ot + at²/2)}/Δt = {v_o(t + Δt − t) + (a/2)(t² + 2tΔt + (Δt)² − t²)}/Δt = {v_oΔt + atΔt + (a/2) Δt} = v_o + at + (a/2)Δt.

Последнее слагаемое при уменьшении Δt становится пренебрежимо малым, поэтому его можно опустить. Таким образом, мы получим известную функцию зависимости скорости от времени при равноускоренном движении:

v = vo + аt.

Аналогично, в принципе, можно вычислять значения мгновенной скорости при любом законе движения. Рассмотрим еще один пример таких вычислений. Пусть закон движения имеет вид х(t) = bt³, где b − некоторая известная постоянная величина. Мгновенную скорость вычисляем посредством следующих преобразований:

v(t) = (x(t + Δt) − x(t))/Δt = (b(t + Δt)³ − bt³)/Δt = {b(t³ + 3t²Δt + 3t(Δt)² + (Δt)³ − t³)}/Δt = 3bt² + 3btΔt + (Δt)².

В этом случае можно пренебречь двумя последними слагаемыми, которые становятся пренебрежимо малыми при уменьшении Δt. Таким образом, в этом случае зависимость скорости от времени имеет вид v(t) = 3bt².

По определению ускорения, вычислим:

a = (v(t + Δt) − v(t))/Δt = (3b(t + Δt) − 3bt²)/Δt = 3b(t² + 2tΔt + (Δt)² − t²)/Δt = 6bt + 3bΔt.

Пренебрегая последним слагаемым, получим выражение для мгновенного ускорения:

а = 6bt.

Подобные вычисления, в принципе, можно проводить для любого закона движения. Методика таких преобразований хорошо разработана в высшей математике, и для всех известных функций расчет отношения приращения функции к приращению аргумента выполняется по достаточно простым правилам вычисления так называемых производных.

Поэтому говорят, что мгновенная скорость является первой производной от зависимости координаты от времени, ускорение первая производная от скорости, или вторая производная от координаты.

К сожалению, у нас нет возможности использовать аппарат высшей математики в данном курсе (так как вы с ним просто незнакомы), поэтому мы будем ограничиваться примерами, где можно обойтись без высшей математики.

¹Эта запись x(t) обозначает координату x в момент времени t.

8.2. Определение закона движения по известной зависимости скорости от времени

Сейчас мы покажем, что по известной произвольной зависимости скорости движения от времени и начальному положению можно, в принципе, найти закон движения. Решение этой задачи может вызвать определенные математические проблемы, но, подчеркнем, эта задача разрешима.

Пусть материальная точка движется вдоль прямой, вдоль которой направим координатную ось X. Допустим, каким-то образом нам стала известна зависимость скорости материальной точки от времени, задаваемая функцией v(t). Проблема заключается в построении закона движения материальной точки, т. е. в определении координаты точки x(t) в произвольный момент времени t. Эта задача может быть разрешена следующим образом: мысленно разобьем время движения на N малых интервалов времени Δt, где i − номер интервала времени, пробегающий ряд натуральных чисел: i = 1,2, 3...N (рис. 53).

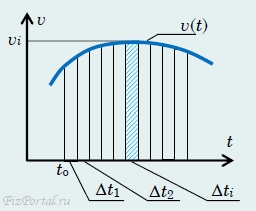
рис. 53

Ясно, что сумма всех временных промежутков должна быть равна рассматриваемому временному интервалу:

Δt₁ + Δt₂ + Δt₃ +... + Δt_N = t − t_o.

Если выбранные промежутки времени достаточно малы, можно пренебречь изменением скорости в течение этого промежутка времени. Тогда изменение координаты за малый промежуток времени Δt_i, приближенно можно считать равным:

Δх_i = v(t_i)Δt_i,

где v(t_i) − средняя скорость на рассматриваемом промежутке времени. Если в момент времени  t_o координата точки равна х_o, то в момент времени t координата точки рассчитывается по формуле

х(t) = х_o + Δх₁ + Δх₂ + Δх₃ + ... + Δх_N = х_o + v₁Δt₁ + v₂Δt₂ + v₃Δt₃ + ... + v_NΔt_N.

Естественно, что чем меньше длина выбранных интервалов времени Δt_i, тем с большей точностью мы найдем координату точки в момент времени t. Следовательно, выбирая интервалы все более малыми, мы можем рассчитать координату точки с любой наперед заданной точностью. Таким образом, нахождение закона движения сводится к утомительной математической процедуре. К счастью, давно разработаны методы вычисления подобных сумм для произвольных зависимостей скоростей от времени. Эти методы составляют суть интегрального исчисления. Примененный нами графический метод определения закона движения фактически является одним из способов вычисления подобных сумм. Подчеркнем, что проблема вычисления подобных сумм является математической, физический смысл которой вполне очевиден − на бесконечно малом интервале времени движение приблизительно равномерное.

Подобный подход − разбиение на очень малые интервалы с последующим суммированием − чрезвычайно широко распространен в различных физических теориях. В дальнейшем мы будем им постоянно пользоваться. Поэтому имеет смысл использовать специальные обозначения для различных сумм, которые очень давно используются в математике. Для обозначения операции суммирования используется специальный символ Σ − греческая буква «сигма» (рис. 54). С использованием этого символа любая сумма записывается в виде

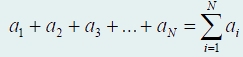
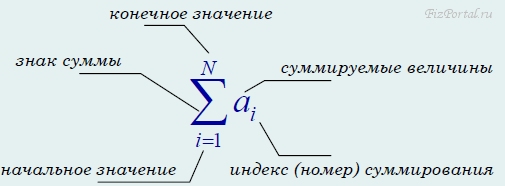
рис. 54

Снизу и сверху суммы указываются пределы изменения номера слагаемого (индекса суммирования). В тех случаях, когда пределы суммирования очевидны, ограничиваются более краткой записью, указывая только обозначение индекса суммирования:

С использованием обозначения суммы формула для расчета закона движения кратко может быть записана в виде

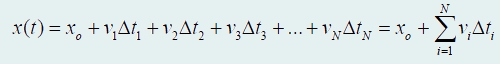
Подчеркнем очень важное обстоятельство: для однозначного определения закона движения мало знать зависимость скорости от времени v(t), необходимо еще одно начальное условие − значение координаты х_o в некоторый момент времени t_o.