5.1. Расчет средней скорости

Составители различных сборников задач по физике очень любят задачи, в которых требуется рассчитать среднюю скорость (чаще всего путевую) на всем интервале движения, когда заданы значения скоростей на отдельных интервалах. Рассмотрим методику решения таких задач.

Прежде всего запомните определение: средняя путевая скорость равна отношению всего пройденного пути ко всему времени движения. Так как это определение, то дискутировать о правильности такого определения нет смысла.

1. Известно, что в течение промежутка времени Δt₁ тело двигалось со скоростью v₁; потом в течение промежутка времени Δt₂ − со скоростью v₂; потом в течение промежутка времени Δt₃ − со скоростью v₃ и так далее (пока у автора задачи не заговорит совесть). Мы же остановимся на трех интервалах. Необходимо рассчитать среднюю скорость за все время движения.

Считая, что на каждом участке скорость постоянна, найдем весь путь, пройденный телом:

S = S₁ + S₂ + S₃ = v₁Δt₁ + v₂Δt₂ + v₃Δt₃. (1)

Очевидно, что время движения равно сумме времени движения на всех интервалах:

t = Δt₁ + Δt₂ + Δt₃. (2)

По определению, средняя скорость за все время движения будет равна:

v_cp = (v₁Δt₁ + v₂Δt₂ + v₃Δt₃)/(Δt₁ + Δt₂ + Δt₃). (3)

В общем случае, средняя скорость не равна среднему арифметическому скоростей на отдельных интервалах. Только в том случае, когда эти временные интервалы равны (Δt₁ = Δt₂ = Δt₃), из формулы (3) следует, что средняя скорость равна среднему арифметическому:

v_cp = (v₁Δt₁ + v₂Δt₁ + v₃Δt₁)/(Δt₁ + Δt₁ + Δt₁) = (v₁ + v₂ + v₃)/3. (4)

2. Известно, что тело прошло участок пути S₁ со скоростью v₁, потом участок пути S₂ со скоростью v₂, наконец, участок пути S₃ со скоростью v₃. Рассчитаем среднюю скорость за все время движения.Понятно, что весь пройденный путь равен:

S = S₁ + S₂ + S₃. (5)

Несложно найти и время движения (если не забыли, что при равномерном движении время равно отношению пути к скорости):

t = Δt₁ + Δt₂ + Δt₃ = S₁/v₁ + S₂/v₂ + S₃/v₃. (6)

Теперь подставим эти выражения в формулу для средней скорости и получим достаточно громоздкое выражение:

v_cp = S/t = (S₁ + S₂ + S₃)/(S/v₁ + S/v₂ + S/v₃). (7)

Этой формуле можно придать более красивый вид:

(S₁ + S₂ + S₃)/v_cp = S₁/v₁ + S₂/v₂ + S₃/v₃. (8)

Мы уже отмечали, что величина, обратная скорости, имеет смысл времени, которое необходимо для преодоления единицы пути.

Назовем¹ эту величину «проходимостью». Тогда если отдельные участки пути одинаковы

S₁ = S₂ = S₃,

то из формулы (8) следует, что средняя «проходимость» равна среднему арифметическому от «проходимостей» на различных одинаковых по длине участках:

1/v_cp = (1/3) × (1/v₁ + 1/v₂ + 1/v₃). (9)

§ 6. Ускорение при движении точки по прямой

После того как мы разобрались с понятием мгновенной скорости (скорости в данный момент времени), у нас появилась возможность говорить об изменении скорости, определить физическую величину, описывающую это изменение. Пусть в момент времени t_o скорость точки была v_o, а в момент времени t₁ > t_o стала равной v₁. Тогда отношение изменения скорости к промежутку времени, в течение которого это изменение произошло, называется ускорением точки¹:

a = (v₁ − v₂)/(t₁ − t_o) = Δv/Δt. (1)

Можно сказать, что ускорение − это скорость  изменения скорости тела.

Ускорение − физическая величина, размерность которой есть отношение размерности скорости к размерности времени, поэтому в СИ размерность ускорения

[a] = [v]/[t] = (м/с)/с = м/с²,

то есть «метр разделить на секунду в квадрате», или «метр в секунду за секунду».

Обсуждая данное определение, мы должны повторить все наши рассуждения, касающиеся перехода от понятия средней к понятию мгновенной скорости. Так, возможны ситуации, когда отношение Δv/Δt не зависит от величины интервала Δt − в этом случае ускорение является постоянной величиной и такое движение называется равноускоренным. Если же величина Δv/Δt зависит от промежутка времени, то формула (1) дает значение среднего ускорения на интервале времени от t_o до t₁. Для более детального описания движения необходимо рассмотреть предельный переход к малому промежутку времени. В этом случае предельное значение отношения Δv/Δt будет являться мгновенным ускорением, или ускорением «в данный момент времени».

При таком определении необходимо повторить все замечания о математическом и физическом смысле предельного перехода Δt → 0, однако они полностью аналогичны рассуждениям о мгновенной скорости, поэтому проведите их самостоятельно.

Заметим, что ускорение, как и скорость, может быть как положительным, так и отрицательным. Напомним, что знак скорости указывает направление движения. Смысл знака ускорения иной − он показывает направление изменения скорости. Рассмотрим возможные комбинации знаков скорости и ускорения.

l) v > 0, a > 0: тело движется в положительном направлении выбранной оси, изменение скорости также положительно, то есть скорость возрастает, иными словами − тело ускоряется.

2) v > 0, а < 0: тело движется в положительном направлении оси, но его скорость убывает − тело притормаживает.

3) v < 0, а > 0: тело движется в отрицательном направлении, но его скорость увеличивается, следовательно, уменьшается по абсолютной величине: тело, двигаясь в отрицательном направлении, притормаживает.

4) v < 0, а < 0: тело движется в отрицательном направлении, при этом его скорость уменьшается, но по абсолютной величине возрастает − тело движется ускоряясь.

Рассмотрим теперь геометрический смысл мгновенного ускорения. Для этого построим график зависимости v_o скорости от времени для некоторой движущейся точки (на рис. 46 − плавная кривая A_oA₁).

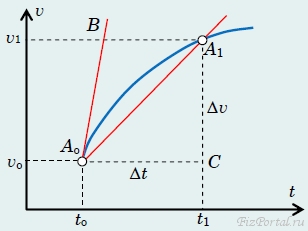
рис. 46

Пусть в момент времени  t_o скорость тела равна v_o (точка А_o на графике), а в момент времени t₁ − скорость v₁ (точка А₁ на графике). В прямоугольном треугольнике А_oA₁С отношение длин катетов

|A₁C|/|A_oC| = Δv/Δt

(то есть среднее ускорение) численно равно тангенсу угла наклона секущей A_oA₁ к оси времени.

При уменьшении интервала времени (то есть при t₁ → t_o) секущая А_oА₁ стремится к касательной А_oВ. Следовательно, тангенс угла наклона касательной к графику зависимости скорости от времени численно равен мгновенному ускорению.

Обязательно следует отметить, что к выражению «тангенс угла наклона» (как и в случае скорости) необходимо относиться с физической, а не с геометрической точки зрения: длины рассматриваемых катетов являются физическими величинами, имеющими различную размерность, поэтому и «тангенс» имеет размерность, в данном случае, ускорения. Поэтому в дальнейшем мы будем использовать термин «коэффициент наклона» касательной к оси времени.

¹Мы будем обозначать ускорение латинской буквой a как сокращение английского слова acceleration − ускорение (кстати, слово «акселерация» происходит от того же корня).