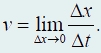§ 5. Средняя и мгновенная скорость при движении точки по прямой

Как мы уже отмечали, равномерное движение является простейшей моделью механического движения. Если такая модель неприменима, то необходимо использовать более сложные. Для их построения нам необходимо ввести и рассмотреть понятие скорости в случае неравномерного движения.

Пусть материальная точка движется так, что ее закон движения имеет вид плавной кривой АСВ (рис. 40).

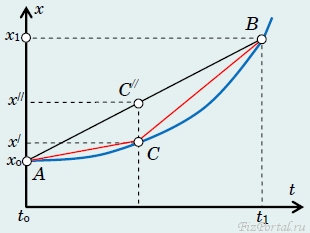
рис. 40

За интервал времени от t_o до t₁ координата точки изменилась от х_o до х₁. Если мы вычислим скорость по прежнему правилу

v_cp = Δx/Δt = (x₁ − x_o)/(t₁ − t_o). (1)

и запишем уравнение закона движения как для равномерного движения

х = х_o + v_сp(t − t_o), (2)

то эта функция будет совпадать с реальным законом движения только в крайних точках интервала, там, где прямая АВ (которая описывается уравнением (2)) пересекается с кривой АСВ. Если же мы захотим вычислить по формуле (2) координату точки в промежуточный момент времени то получим значение х^//, которое может заметно отличаться от истинного значения х^/. Таким образом, скорость (она называется средней скоростью), вычисленная по формуле (1), в данном случае характеризует быстроту перемещения точки на всем интервале в среднем, но она не позволяет вычислять координаты точки в произвольный момент времени.

Средней скоростью называется физическая величина, равная отношению изменения координаты точки к интервалу времени, в течение которого это изменение произошло.

Геометрический смысл средней скорости − коэффициент наклона секущей АВ графика закона движения.

Для более детального, более точного описания движения можно задать два значения средней скорости:

а) на промежутке времени от t_o до t^/

v_cp1 = (x^/ − x_o)/(t^/ − t_o);

б) на промежутке времени от  t^/ до t₁

v_cp2 = (x₁ − x^/)/(t₁ − t^/).

Если по этим двум средним скоростям построить закон движения, то он будет изображаться ломаной АСВ, которая точнее описывает реальное движение точки. А если и такая точность нас не устраивает, то необходимо дробить временные интервалы дальше − на четыре, восемь и т. д. частей. При этом необходимо задавать соответственно четыре, восемь и т. д. значений средних скоростей. Согласитесь, такое описание становится громоздким и неудобным. Выход из этой ситуации давно найден − он заключается в том, что нужно рассматривать скорость как функцию времени.

Давайте посмотрим, как будет меняться средняя скорость при уменьшении промежутка времени, за который мы эту скорость вычисляем. Будем вычислять среднюю скорость за интервал времени от t_o до t₁, последовательно приближая значение к t_o. При этом семейство секущих А_oA₁, А_oA₁^/, А_oA₁^// (рис. 41)

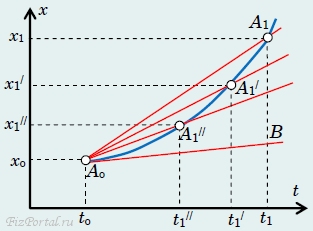
рис. 41

будет стремиться к некоторому предельному положению прямой А_oB, которая является касательной к графику закона движения. Приведем иной пример закона движения, чтобы показать, что  мгновенная скорость может быть как больше, так и меньше средней скорости (рис. 42 с теми обозначениями, что и на рис. 41).

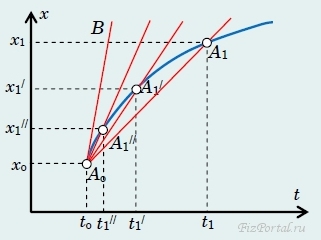
рис. 42

Процедуру уточнения описания движения можно показать и алгебраически, последовательно вычисляя отношения

v_cp = (x₁ − x_o)/(t₁ − t_o), v_cp^/ = (x₁^/ − x_o)/(t₁^/ − t_o), v_cp^// = (x₁^// − x_o)/(t₁^// − t_o).

При этом оказывается, что эти величины приближаются к некоторому вполне определенному значению. Это предельное значение получило название мгновенной скорости.

Мгновенной скоростью называется отношение изменения координаты точки к интервалу времени, за которое это изменение произошло, при интервале времени, стремящемся к нулю¹:

v = Δx/Δt при Δt → 0. (3)

Геометрический смысл мгновенной скорости − коэффициент наклона касательной к графику закона движения.

Таким образом, мы «привязали» значение мгновенной скорости к конкретному моменту времени − задали значение скорости в данный момент времени в данной точке пространства. Тем самым у нас появилась возможность рассматривать скорость тела как функцию времени, или функцию координаты.

С математической точки зрения это гораздо удобней, чем задавать значения средних скоростей на многих малых временных промежутках. Давайте задумаемся: а имеет ли физический смысл − скорость в данный момент времени? Скорость − характеристика движения, в данном случае − перемещения тела в пространстве. Для того чтобы зафиксировать перемещение, необходимо наблюдать за движением в течение некоторого промежутка времени. Чтобы измерить скорость, также необходим промежуток времени. Даже самые совершенные измерители скорости − радарные установки − измеряют скорость движущихся автомобилей пусть за малый (порядка одной миллионной доли секунды) промежуток, но не в какой-то момент времени. Следовательно, выражение «скорость в данный момент времени» с точки зрения физики некорректно. Тем не менее в механике постоянно пользуются понятием мгновенной скорости, которое очень удобно в математических расчетах. Математически, логически мы можем рассмотреть предельный переход Δt → 0, а физически имеется минимально возможное значение промежутка Δt, за который можно измерить скорость.

Однако если мы изучаем движение автомобиля в течение нескольких часов, то промежуток времени в одну секунду может считаться бесконечно малым.

Таким образом, понятие мгновенной скорости является разумным компромиссом между простотой математического описания и строгим физическим смыслом. Такие «компромиссы» нам будут встречаться в ходе изучения физики постоянно.

В дальнейшем, говоря о скорости, мы будем иметь в виду именно мгновенную скорость. Заметим, при равномерном движении мгновенная скорость равна ранее определенной скорости потому, что при равномерном движении отношение Δx/Δt не зависит от величины промежутка времени, поэтому остается неизменным и при сколь угодно малом Δt.

Так как скорость может зависеть от времени, то ее следует рассматривать как функцию времени и изображать ее в виде графика.

При равномерном движении с постоянной скоростью у график зависимости скорости от времени является прямой линией, параллельной оси времени (на рис. 43 − прямая АВ).

Рассмотрим промежуток времени от t_o до t₁. Произведение величины этого интервала (t₁ − t_o) на скорость v_o равно, с одной стороны изменению координаты Δx, а сдругой − площади прямоугольника под графиком зависимости скорости от времени.

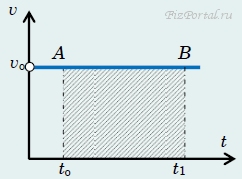
рис. 43

Площадь под графиком следует понимать, опять же таки в физическом смысле, как произведение физических величин, имеющих различную размерность, а не в чисто геометрическом смысле − как произведение длин отрезков.

Покажем, что площадь под графиком зависимости скорости от времени равна изменению координаты при любой зависимости скорости от времени v(t). Разобьем время движения от t_o до t на малые интервалы величиной Δt; на каждом интервале определим среднюю скорость v₁. Тогда площадь прямоугольника с основанием Δt и высотой v₁ (на рис. 44 он отмечен более плотной штриховкой) будет равна изменению координаты за этот малый промежуток времени. Сумма площадей всех таких прямоугольников (на рис. 44 заштрихованы)

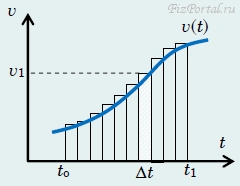
рис. 44

будет равна изменению координаты точки за рассматриваемый промежуток времени движения от t_o до t₁. Если теперь все интервалы времени Δt уменьшать (соответственно увеличивая при этом их число), то суммы площадей прямоугольников будут стремиться к площади криволинейной трапеции под графиком функции v(t).

Дополним наше определение площади под кривой еще одной договоренностью: будем считать, что если кривая лежит t под осью времени (то есть скорость отрицательна), то и соответствующую площадь будем считать отрицательной (рис. 45).

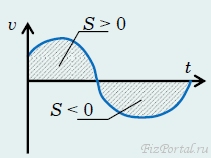
рис. 45

¹В высшей математике это определение записывают с помощью специального символа lim (предел − limit):