Примеры решения задач Задача №1

П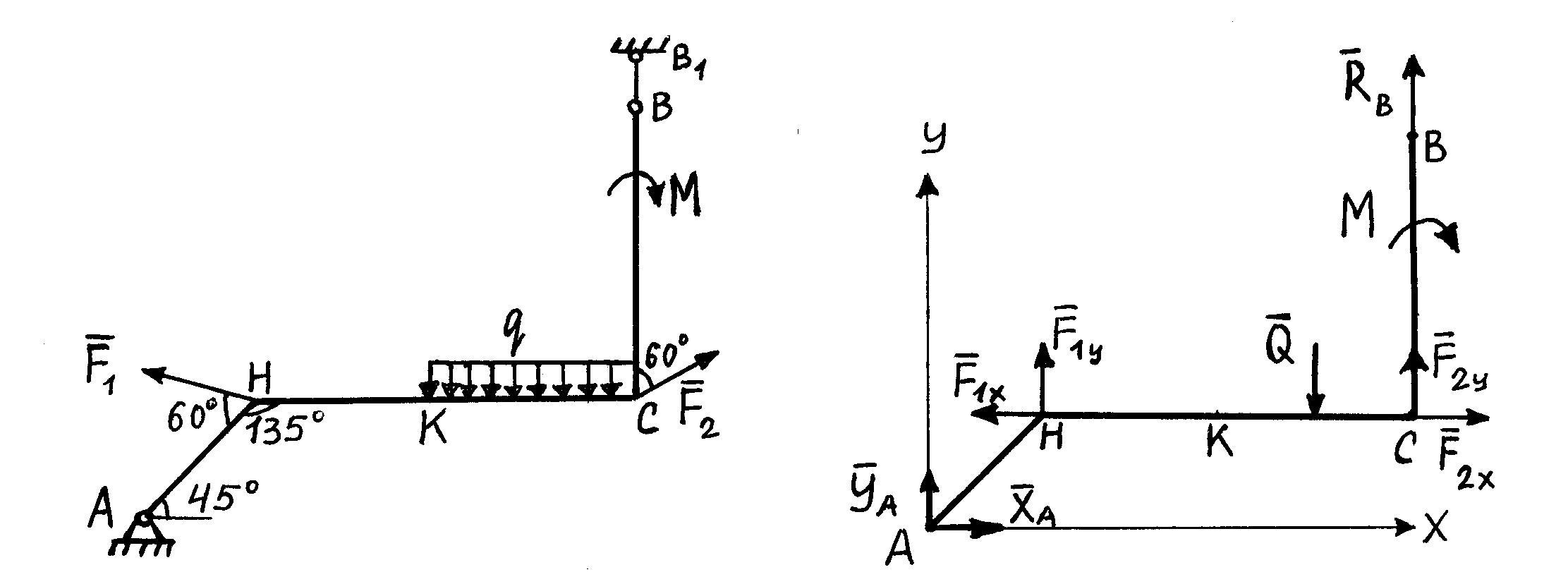 лоская рама (рис.1) закреплена в точке шарнирно неподвижной опорой, а в точке – невесомым стержнем с шарнирами на концах. На раму действуют: пара сил с моментом , силы и равномерно распределённая нагрузка интенсивности . Дано: кН; кН; кН/м; кН∙м; м; м; м.

Определить реакции в точках и .

Рис.1 Рис.2

Решение. Изображаем раму свободной в точках и от связей (рис.2), а их действие заменяем реакциями . Реакцию (она на рисунке не показана) раскладываем на составляющие , . Реакцию направим вдоль невесомого стержня . Распределённую нагрузку заменяем равнодействующей , приложенной посредине отрезка , величиной 1 кН/м м = кН. Силы раскладываем на составляющие, параллельные осям . Модули этих составляющих: = 1 кН∙0,966 = 0,966 кН,

= кН∙0,259 = 0,259 кН; 2 кН∙0,866 = 1,73 кН,

2 кН∙0,5 = 1 кН. Направления составляющих показаны на рис.2. Рама находится в равновесии под действием произвольной плоской системы сил. Составим уравнения равновесия:

1)

2)

3)

Из уравнения 1) находим:

Из уравнений 2) и 3) определяем:

Можно сделать проверку, составив дополнительное уравнение, которое должно обратиться в тождество вида с погрешностью вычислений, не превышающей 1%. Таким уравнением может быть, например,

кН∙м.

Относительная погрешность: < .

Ответ: кН, кН, кН.

Знаки «минус» указывают, что силы и направлены противоположно показанным на рис. 2. Модуль реакции в точке будет: кН.

Задача №2

К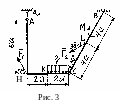 онструкция состоит из жёсткого угольника и стержня , которые в точке соединены шарниром. Угольник в точке соединен с невесомым стержнем. В точке стержень закреплён заделкой. На конструкцию действуют: пара сил с моментом 60 кН∙м, равномерно распределённая нагрузка на участке интенсивности 20 кН/м, сила 20 кН и сила 30 кН. Точки приложения и направления сил показаны на рис.3. В расчётах принять 0,5 м. Определить реакции связей в точках

Р ешение. Конструкцию разъединим в шарнире (рис.4, рис.5), и рассмотрим равновесие угольника и стержня в отдельности. Заменим распределённую силу интенсивности равнодействующей 20 кН, приложенной посредине участка .

Силы разложим на составляющие, модули которых:

10 кН, 17,32 кН,

25,98 кН, 15 кН.

Освободим конструкцию от связей и заменим их действие реакциями . В точке разъединения приложим внутренние силы взаимодействия , при этом считая , .

Составим уравнения равновесия для угольника (рис.4):

1) ;

2) ; 3) .

Решая эту систему, получим: кН;

10 кН; 15 кН.

Сделаем проверку: =

= 10 кН ∙ 3 м + 15 кН ∙ 2 м – 10 кН ∙ 3 м – 20 кН ∙ 1,5 м = 0.

Реакции определены верно.

Составим уравнения равновесия для стержня (рис.5):

4)

;

5) ; 6) .

Решая систему 4) – 6) , получим: 0,866 – ∙ ∙0,5 + + 0,866 – 0,5 + = 94,64 кН∙м; =

= 35,98 кН; 30 кН.

Сделаем проверку:

139,64 кН∙м –

– 139,64 кН∙м = 0.

Ответ: 12,32 кН, 35,98 кН, 30 кН,

94,64 кН∙м, 10 кН, 15 кН.