5.Изгиб:
Понятие изгиб
Изгиб-вид деформации, при котором происходит искривление оси бруса.
Деформация прямого изгиба (плоский), при котором силовая плоскость проходит через одну из главных центров осей сечения
Косой изгиб, при котором силовая плоскость совпадает только с одной центр осью, т.е. проходит под некоторым углом к главным центр.осям .
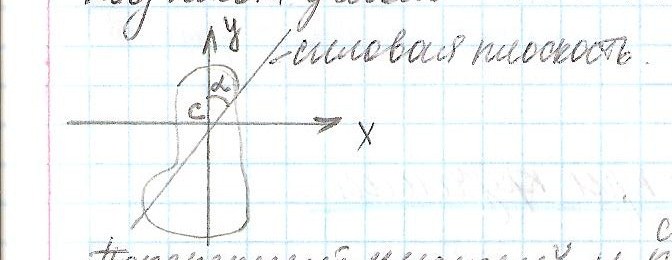
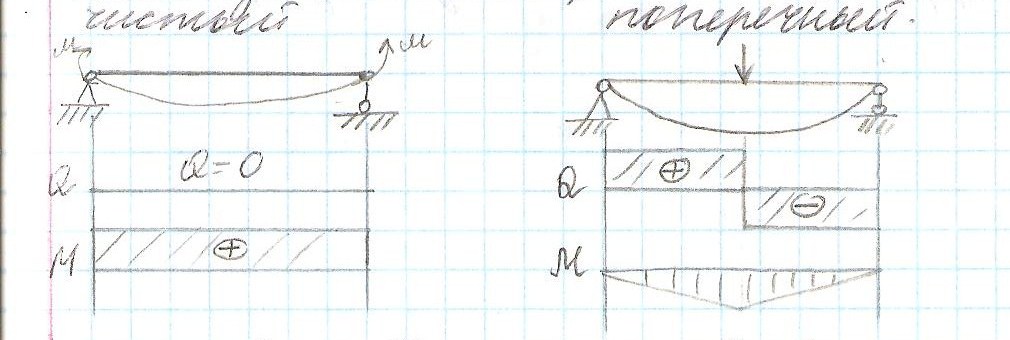
Поперечный, чистый и плоский изгиб.
Чистый изгиб, при котором в сечении балки действует только изгибающий момент, а поперечным называется изгиб, при котором действует как и изгиб момента, так и поперечная сила
Плоский изгиб (плоскость действия нагрузки проходит через главную центр ось инерции сечения)
Напряжения при чистом изгибе
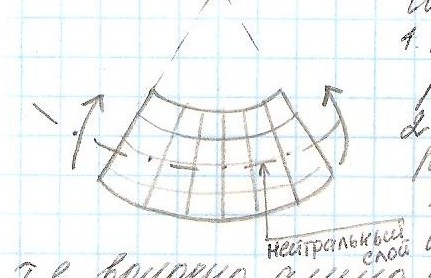
Чистый изгиб характеризуется следующим
На выпуклой стороне волокна растягиваются, а на вогнутой- сжимаются
Переход от сжатых волокон к растянутым и наоборот происходит непрерывно и между ними есть нейтральный слой, т.е. волокна, длина которых при изгибе не изменяется.
В растянутой зоне поперечн.сечения сужаются,а в сжатой – расширяются(эффект Пуассона)
Плоские поперечные сечения, нормальные к упругой линии балки до изгиба, остаются плоскими и нормальными к ней после изгиба(гипотеза плоских сечений) Бернулли.
Продольные волокна не оказывают друг на друга давления, а испыт.только осевое растяжение,сжатие(Ϭу=0)
Нормальные напряжения распределены по ширине сечения равномерно
Связь между нормальным напряжением и изгибающим моментом
Ϭу=(Мизгиб/Yx)*y y-растяжение
Ϭ=Мизгиб/Wx
Условия прочности при чистом и плоском изгибе
Ϭmax=Mx/Wx < =(меньше или равно) [Ϭ]