4.Кручение:

Понятие кручения.

Кручение появится, если неподвижно закрепить, например, левый конец стержня круглого сечения и приложить к правому концу скручивающий момент (М_{скручивания}) относительно оси стержня z. В стержне появится деформация кручения: одно поперечное сечение повернется на некоторый угол относительно другого (растяжение между сечениями останется прежним, если угол поворота мал). В поперечных сечениях, стержня, при кручении, возникает только одно внутреннее усилие – крутящий момент(M_z).

Угол закручивания. Фи – угол, на который повернется крайнее правое поперечное сечение стержня относительно неподвижного левого.

Вал.

Вал — деталь машины, предназначенная для передачи крутящего момента и восприятия действующих сил со стороны расположенных на нём деталей и опор.

Чистый сдвиг.

Чистый сдвиг — напряженное состояние, при котором по взаимно перпендикулярным площадкам (граням) элемента возникают только касательные напряжения. Касательные напряжения, где Q — сила, действующая вдоль грани, F — площадь грани. Площадки, по которым действуют только касательные напряжения, называются площадками чистого сдвига. Касательные напряжения на них — наибольшие. Чистый сдвиг можно представить как одновременное сжатие и растяжение, происходящее по двум взаимно перпендикулярным направлениям. Т.е. это частный случай плоского напряженного состояния, при котором главные напряжения: s₁= — s₃ = t; s₂= 0. Главные площадки составляют с площадками чистого сдвига угол 45^о.

Y=tgY=a/h - относительный сдвиг.

Закон Гука при сдвиге.

Касательные напряжения пропорциональны углу сдвига в определенных пределах упругой деформации сдвига. [МПа]

T(тау)=G*Y , где G – коэффициент пропорциональности, характеризующий жесткость при сдвиге.

Кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси (рис. 5.1).

 

Стержни круглого или кольцевого сечения, работающие на кручение, называют валами. При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.

Пусть вал вращается с постоянной скоростью n об/мин. и передает мощность N Нм/с. Угловая скорость вращения вала равна   (рад/сек), а передаваемая мощность  .

Скручивающий момент равен  .

Если мощность задана в киловаттах, то величина скручивающего момента определяется по формуле

.          

Построение эпюр крутящих моментов

Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала. Крутящий момент М_к в сечении вала числено равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения, при этом могут рассматриваться как левая, так и правая отсеченные части вала.

Примем правило знаков для крутящего момента: его положительное направление соответствует повороту сечения по ходу часовой стрелки, если смотреть на сечение со стороны внешней нормали (рис. 5.2).

                                           Рис.5.2

 

При наличии распределенной моментной нагрузки m (рис.5.3) крутящие моменты М_К связаны дифференциальной зависимостью

                              (5.1)

из которой вытекает следующая формула:

                          (5.2)

где   – крутящий момент в начале участка.

Согласно формуле (5.2) на участках с равномерно распределенной нагрузкой m крутящий момент изменяется по линейному закону. При отсутствии погонной нагрузки (m = 0) крутящий момент сохраняет постоянное значение  (М_К = М_Ко = const). В сечениях, где к валу приложены сосредоточенные скручивающие моменты, на эпюре М_К возникают скачки, направленные вверх, если моменты направлены против часовой стрелки, либо вниз – при обратном направлении моментов.

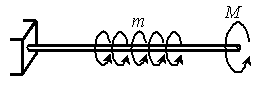
                                Рис. 5.3

Напряжения в поперечном сечении

Опыты показывают, что если на поверхности бруса круглого сечения нанести прямоугольную сетку, а на торцевой поверхности нанести радиальные линии (рис.5.5), то после деформации кручение окажется что:

- все образующие поворачиваются на один и тот же угол  , а прямоугольники, нанесенные на поверхности, превращаются в параллелограммы;

- торцевые сечения остаются круглыми, плоскими, расстояния между ними не меняются;

- каждое сечение поворачивается относительно другого на некоторый угол  , называемый углом закручивания;

- радиальные линии на торцевой поверхности остаются прямыми.

На основании этих наблюдений можно заключить, что может быть принята гипотеза Бернулли (гипотеза плоских сечений), а в вале возникают условия чистого сдвига, в поперечных сечениях действуют только касательные напряжения, нормальные напряжения равны нулю.

Рассмотрим поперечное сечение вала, расположенное на некотором расстоянии z от торцевого, где М_к=T (рис.5.5). На элементарной площадке dF будет действовать элементарная сила  , момент который относительно оси вала равен  . Крутящий момент М_к, в сечении равен

.                                     (5.3)

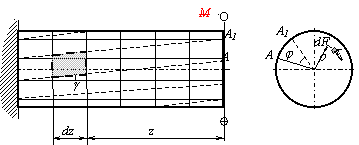
                                                  Рис.5.5

 

Для того чтобы проинтегрировать это выражение необходимо знать закон распределения напряжений в сечении. Выделим из вала элементарное кольцо длиной dz и толщиной   (рис.5.6).

Правый торец элемента повернется относительно левого на угол  , образующая СВ повернется на угол   и займет положение СВ₁. Угол   - относительный сдвиг. Из треугольника ОВВ₁ найдем:

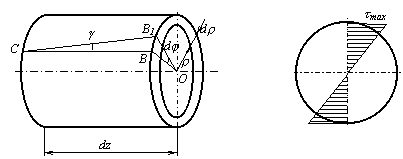
                                Рис.5.6                                                           Рис.5.7

 

.

 Из треугольника СВВ₁:  . Откуда, приравнивая правые части, получим

.

На основании закона Гука при сдвиге:

.                                     (5.4)

Подставим выражение (5.2) в (5.1):

.

Откуда

.                                                  (5.5)

Подставим значение    в выражение (5.4) получим:

.

Таким образом, касательные напряжения при кручении прямо пропорциональны расстоянию от центра тяжести сечения до рассматриваемой точки и одинаковы в точках, одинаково удаленных от центра тяжести сечения (рис. 5.7). При   получим  . Наибольшие напряжения возникают в точках контура сечения при  :

.

Величина отношения полярного момента инерции к радиусу вала называется моментом сопротивления сечения при кручении или полярным моментом сопротивления

.

Для сплошного круглого сечения

.

Для кольцевого сечения

,

где  .

 

Тогда максимальные касательные напряжения равны

.

 

Условие прочности при кручении вала круглого и кольцевого сечения

Условие прочности при кручении с учетом принятых обозначений формулируется следующим образом: максимальные касательные напряжения, возникающие в опасном сечении вала, не должны превышать допускаемых напряжений и записывается в виде

,                            (5.6)

где   берется либо на основании опытных данных, либо (при отсутствии нужных опытных характеристик) по теориям прочности, соответствующим материалу. Например, из теорий прочности для хрупких материалов, примененных для чистого сдвига, следуют такие результаты:

- из второй теории прочности

;                                (5.7)

-  из теории Мора

,                                 (5.8)

где  .

Из теорий прочности для пластичных материалов при чистом сдвиге получим:

- по третьей теории прочности

,                                              (5.9)

- по четвертой теории прочности

.                                           (5.10)

Как следует из закона парности касательных напряжений, одновременно с касательными напряжениями, действующими в плоскости поперечного сечения вала, имеют место касательные напряжения в продольных плоскостях. Они равны по величине парным напряжениям, но имеют противоположный знак. Таким образом, все элементы бруса при кручении находятся в состоянии чистого сдвига. Так как чистый сдвиг является частным случаем плоского напряженного состояния, при котором  ,  ,  , то при повороте граней элемента на 45⁰ в новых площадках обнаруживаются только нормальные напряжения, равные по величине    (рис.5.8).

Рассмотрим возможные виды разрушения валов, изготовленных из различных материалов при кручении. Валы из пластичных материалов чаще всего разрушаются по сечению, перпендикулярному к оси вала, под действием касательных напряжений, действующих в этом сечении (рис.5.9,а). Валы из хрупких материалов, разрушаются по винтовой поверхности наклоненной к оси вала под углом 45⁰, т.е. по направлению действия максимальных растягивающих напряжений (рис.5.9,б). У деревянных валов первые трещины возникают по образующим цилиндра, так как древесина плохо сопротивляется действию касательных напряжений, направленных вдоль волокон (рис.5.9,в).

 

           

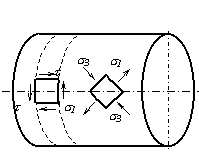
                        Рис.5.8                                                            Рис.5.9

 

Таким образом, характер разрушения зависит от способности материала вала сопротивляться воздействию нормальных и касательных напряжений. В соответствии с этим, допускаемые касательные напряжения принимаются равным   - для хрупких материалов и    - для пластичных материалов.

 

Деформации при кручении и условие жесткости вала

Из выражения (5.5) следует, что

,

интегрируя которое по длине вала, получим:

.

Если М_к = const и  = const по всей длине вала, то

,

где   - жесткость вала при кручении.

Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания

.

Для обеспечения требуемой жесткости вала необходимо, чтобы наибольший относительный угол закручивания не превосходил допускаемого:

.         

Эта формула выражает условие жесткости вала при кручении. Обычно принимается   на 1 м длины вала.

 

Расчеты на прочность и жесткость валов круглого и кольцевого сечений

При расчетах на прочность при кручении (также как и при растяжении) могут решаться три задачи:

а) проверочный расчет – проверить, выдержит ли вал приложенную нагрузку;

б) проектировочный расчет - определить размеры вала из условия его проч­ности;

в) расчет по несущей способности - определить максимально допустимый крутящий момент.

- При проверочном расчете на прочность рекомендуется следующий порядок расчета валов при кручении:

1) по схеме вала и действующим на него скручивающим моментам строят эпюру внутренних крутящих моментов по отдельным участкам;

2) выбирают материал для рассчитываемого вала и определяют для этого ма­териала допускаемое напряжение, например по формуле (5.9),  ;

3) для участка вала с максимальным по модулю значением крутящего момента записывают условие прочности при кручении

                                      

- Проектировочный расчет проводится, исходя из условия прочности на основе следующего соотношения:

                                                           

Для сплошного круглого сечения  , отсюда можем записать вы­ражение для определения диаметра вала из условия его прочности:

                                                   

Для кольцевого сечения

Определив размеры вала из условия прочности, проверяют вал на жесткость.

Условие жесткости требует, чтобы максимальный относительный угол закручивания  , был меньше или в предельном случае равен допускаемому углу закручивания единицы длины вала, т.е.

 .                               (5.11)

Из условия прочности можно найти необходимый для обеспечения прочности полярный момент сопротивления сечения, а по нему и диаметр вала:

 но W_ρ = 0,2d³, поэтому

                                                       (5.12)

Из формулы (5.11) можно найти необходимый полярный момент инерции сечения, а по нему и диаметр вала

В этой формуле допускаемый относительный угол закручивания   должен быть выражен в радианах; если этот угол дан в градусах, то соотношение для определения I_p  будет выглядеть следующим образом:

но I_p = 0,1d ⁴ , поэтому

                                   (5.13)

Из двух диаметров, рассчитанных по формулам (5.12) и (5.13), в качестве окончательного диаметра выбирается больший, который обычно округляется до целых миллиметров.

В случае расчета размеров вала кольцевого поперечного сечения при заданном соотношении внутреннего d_вн и наружного диаметров d, т.е. при заданном параметре k = d_вн /d, формулы  (5.12) и (5.13) принимают вид:

                                        (5.14)

                       (5.15)

 

Потенциальная энергия деформации при кручении.

Элементарная работа статически приложенного внешнего момента Т на перемещении    равна:

.

При чистом кручении М_к = Т и  .

Потенциальная энергия деформации

;

интегрируя выражение для элементарной работы по всей длине l стержня, получим

.

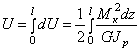При М_к = const и  = const, получим

.