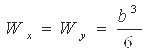2.Геометрические характеристики сечений:

Рассмотрим фигуру площади А(рис 1). Выделим на ней элементарную площадку dA с координатами х,у и радиусом-вектором р.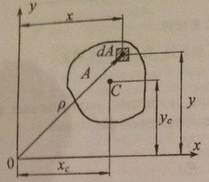

Статическими моментами инерции фигуры относительно осей х и у называются величины Sх и Sу, определяемые интегралами: , где х,у-расстояние от элементарной площадки dA до осей Ох,Оу.

Можно показать,что координаты центра тяжести фигуры Хс и Ус вычисляются по формулам: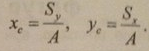

Оси, проходящие через центр тяжести фигуры, называются центральными осями. Для центральных осей Хс=Ху=0,а значит, что для центральных осей статические моменты инерции равны нулю (Sx=Sy=0).

Величины называются осевыми моментами инерции фигуры относительно осей х,у соответственно.

Интеграл по площади фигуры называется полярным моментом инерции.

Величина - центробежный момент инерции фигуры.

Учитывая, что получаем .

Следовательно т.е. сумма осевых моментов инерции сечения равна полярному моменту инерции этого сечения.

Осевые о полярные моменты инерции всегда положительны, центробежный момент инерции может быть положительным ,отрицательным, равным нулю.

Центробежный момент инерции фигуры относительно осей ,хотя бы одна из которых является осью симметрии, равен нулю. Действительно, для симметричной фигуры всегда можно выделить два элемента её площади (рис 2)

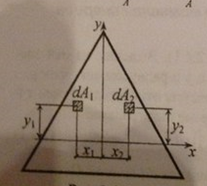
,которые имеют одинаковые ординаты у1=у2=у и равные по величине, но противоположные по знаку абсциссы х1== и х2=-х. В этом случае

Моменты инерции для простейших фигур (прямоугольник, круг, квадрат).

Прямоугольник. Определим момент инерции сечения относительно оси Ох, проходящей через центр тяжести прямоугольника высокой h и шириной b (рис3) . Выделив из прямоугольника элементарную площадку ,получим .

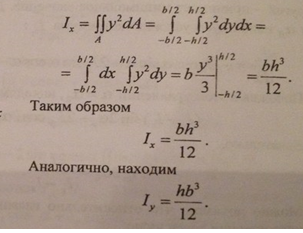Круг. Определим полярный момент инерции круга относительно его центра 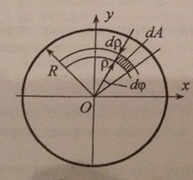. В полярной системе координат Следовательно,

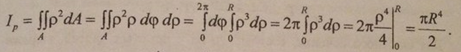
Таким образом В силу симметрии круга Ix=Iy. Учитывая, что , получаем

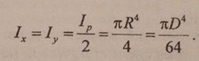
Квадрат.

Форма поперечного сечения	Момент инерции	Момент сопротивления	Радиус инерции

Осевой и полярные моменты сопротивления:

Осевым моментом сопротивления называется отношение момента инерции относительно данной оси к расстоянию от оси до наиболее удаленной точки поперечного сечения. Wx= Jx/Ymax Wy= Jy/Xmax

Полярным моментом сопротивлением называют отношение полярного момента инерции к расстоянию от полюса до наиболее удаленной точки сечения.

Wp=Yp/Pmax в качестве полюса принимается центр тяжести поперечного сечения стержня.

3.Осевое растяжение-сжатие:

Внутренние силы при растяжении - сжатие :

Растяжение – сжатие - это вид нагружения, при которых в поперечных сечениях возникает только продольные силы N, а прочее силовые факторы = 0. Продольная сила – внутренние усилие ,равное сумме проекций всех внешних сил, взятых с одной стороны от сечения, на ось стержня.

σ = N/A [кг/см^2] (σ- напряжение. A- площадь)

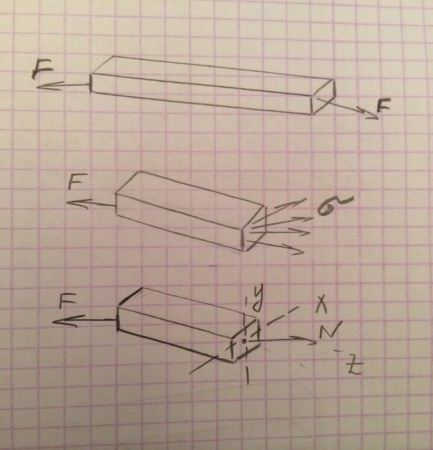
Пластичные и хрупкие материалы :

К пластичным относятся материалы, разрушение которых предшествуют большие остаточные деформации достигающие иногда 20..25 % (Al,малоуглеродные).

Хрупкими называют материалы, разрушающиеся при малых остаточных деформациях, не превышающих 2..5 % (чугун,стекло)

Понятие упругости и пластичности :

Упругость – свойство материалов под действием механических напряжений деформируется обратимо: после снятия напряжений материал остается недеформированным.

Пластичность- способность материала без разрушения получать большие остаточные деформации.

Остаточная деформация - это деформация, которая после прекращения действий внешние силы сохраняется в деформируемом теле в виде пластических деформаций.

ДЕФОРМАЦИЯ:

Деформация – (от латинского искажение ) изменение взаимного положения частиц, связанное с их перемещением относительно друг друга. Изменение формы и размеров тела под действием внешних сил, температуры,P.

Диаграмма растяжения и сжатия.

Диаграмма испытания пластичной стали а):

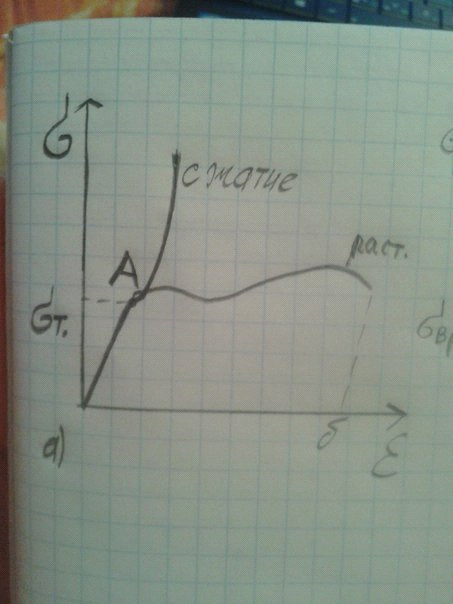
Диаграмма хрупкого материала б):

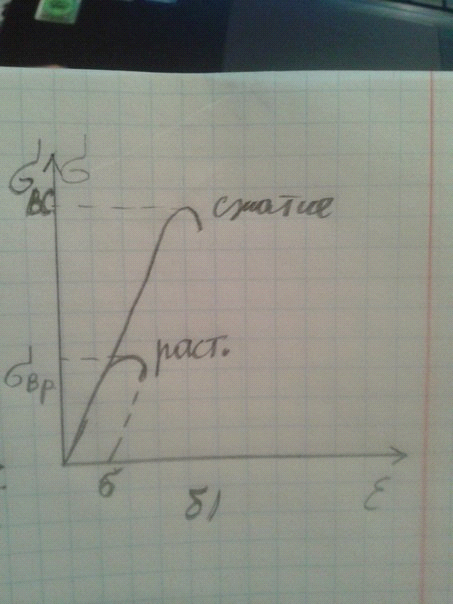
Основные зоны.

Условная диаграмма растяж. пластичной стали:

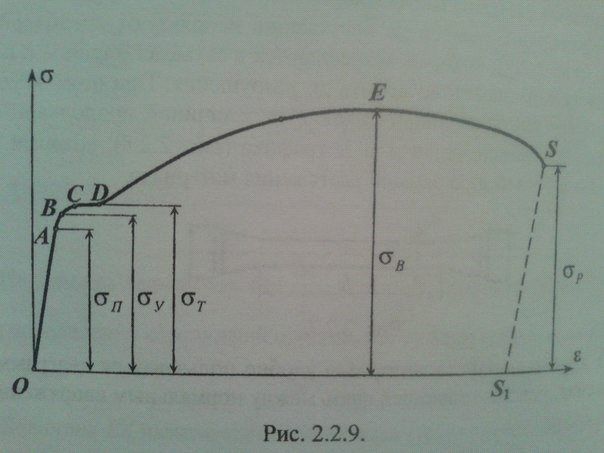
Предел пропорциональности- это наибольшее напряжение, при котором деформация в материале прямо пропорциональна нагрузке:

σп=Fп/Aо , где Ao-площадь. Ао=Пdo^2/4

Предел упругости- это наибольшее напряжение, при котором в материале возникает только упругая деформация: σу=Fу/Ao

Предел текучести- это напряжение, при котором деформация возрастает без заметного увеличения нагрузки (горизонтальный участок СД): σт=Fт/Ao

Предел прочности- напряжение, соответствующее макс. нагрузке, которую выдержал образец не разрушаясь: σВ=FB/Ao

Истиное сопротивление по разрыву: σр=Fр/Aш

Модуль упругости, коэффициент Пуассона.

Модуль упругости(модуль Юнга)- физ. величина, харак-щая св-ва материалов сопротивляющийся растяжению и сжатию при упругой деформации: Е=σ/ε E=(F*L)/S*ΔL

Коэфф. Пауссона- абсолютная вел. отношения поперечной образца материала. Не зависит от размеров тела.Зависит от природы материалов. μ=!ε`/ε!

Закон Гука при растяжении-сжатии.

Деформация пропорциональна нагрузке. Выражаем прямую пропорциональность м/у напряжением и относительной деформ.: σ=Еε

Условие прочности:

σmax=Nmax/A ≤ ¦σ¦ , ¦σ¦-допустимое напряжение

¦σ¦=σ0/n , где σ0- предельное (опасное) напряжение. n-коэффициент запаса прочности. nрастяжения=1.5 -:- 2 ; nсжатия = 2-:- 5

Для пластичных мат-ов за предельное (опасное) напряжение σ0 , принимается предел текучести σт.

Для хрупких - принимается предел прочности σВ

Основные типы расчетов на прочность:

Проверка прочности(проверочный расчет).

G_maх = N_maх /A <= [G]

Подбор сечения(проектировочный расчет).

A>=N_max / [G]

Определение грузоподъемности(допускаемая нагрузка).

N_max <= [G]*A