3. Естественный способ задания движе­ния точки.

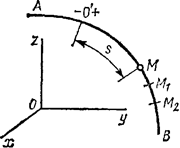
Рис.5

 

Естественным способом задания движения удобно пользоваться в тех слу­чаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ явля­ется траекторией точки М при ее движении относительно системы отсчета Oxyz (рис.5) Выберем на этой траектории какую-нибудь неподвижную точку О', которую примем за начало отсчета, и установим на траектории положительное и отрицатель­ное направления отсчета (как на координат­ной оси).

Тогда положение точки М на тра­ектории будет однозначно определяться криволинейной коорди­натой s, которая равна расстоянию от точки О’ до точки М, изме­ренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка М перемещается в положения M₁, М₂,... . следовательно, расстояние s будет с течением времени изменяться.

Чтобы знать положение точки М на траектории в любой момент времени, надо знать зависимость

s=f(t).

Уравнение выражает закон движения точки М вдоль тра­ектории.

 

Пример 2. Точка движется по прямой линии, по закону s=2t+3 (см) (рис. 6).

Рис.6

 

В начале движения, при t=0   s=OM₀=s₀=3 см. Положение точки M₀ назы­вается начальным положением.  При  t=1 с,   s=OM₁=5 см. 

Конечно, за 1 сек. точка прошла расстоя­ние  M₀M₁=2 см. Так  что  s – это не путь пройденный точ­кой, а расстояние от начала отсчёта до точки.

Скорости и ускорения точки при различных способах задания движения

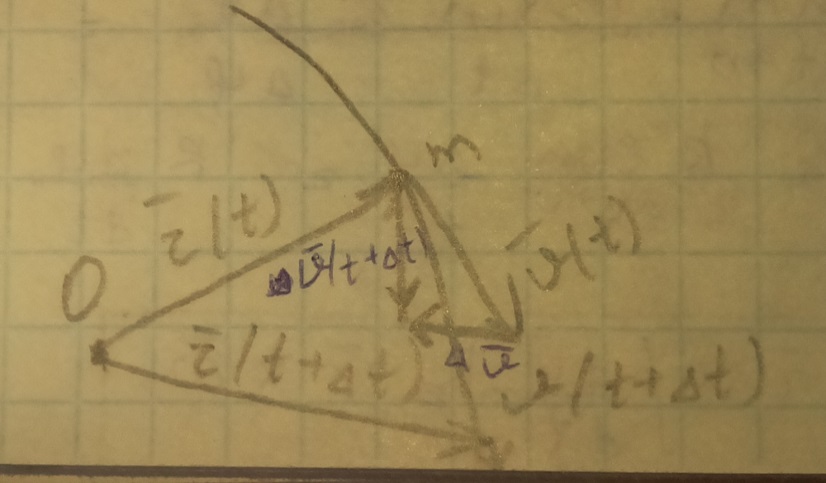
1. Векторный: пусть точка m движется по линии, выбрав начало отсчета О. Тогда положение точки определяет (t). = (t)- закон движения.

скорость точки направлена по касательной.

(1)называется ускорением точки.

Определим направление ускорения. Для этого перенесем вектор параллельно. Из формулы (1) следует, что направление вектора и направление ускорения совпадают. направлен в сторону вогнутой области, следовательно вектор ускорения тоже направлен в сторону вогнутости траектории.

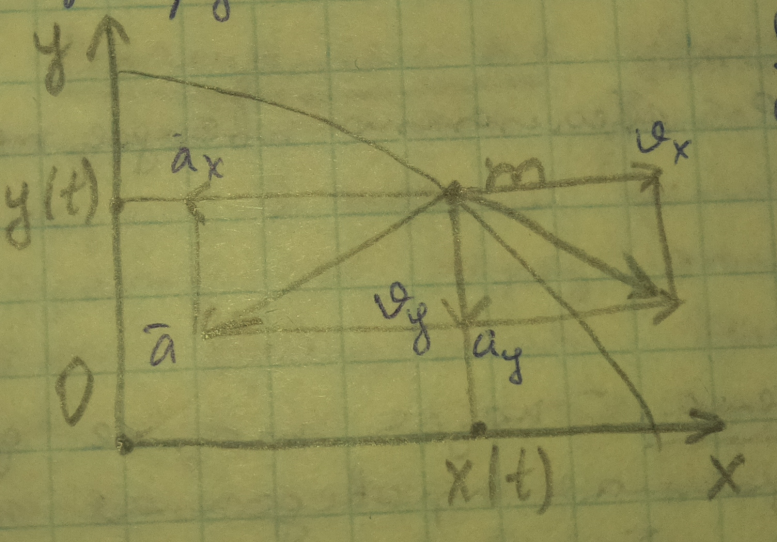
2. Координатный: x=x(t)

y=y(t), является законом движения , исключает t , получаем: y=y(x)-уравнение траектории движения .

V_X=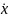

V_Y= ,-проекции, координаты скорости

= V_X+ V_Y

a_x= _x проекция ускорения

a_y= _y ускорение всегда направлено в сторону вогнутости

_x+ _y

a=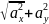

3. Естественный способ:

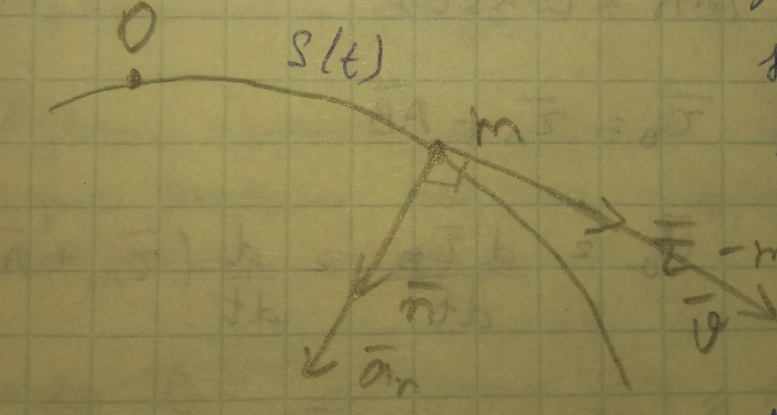
Пусть m движется по линии . на этой линии определить начало отчета (о). тогда положение точки определяется S(t). S=S(t)-является законом движения. Введем естественную систему координат .

τ- орт касательной (тау)

ň-нормаль

I I=I I=1

• перпендикуляр

a= (dV/dt)=(d/dt)(Vr)=(dV/dt)r+V(dr/dt)

(dV/dt)r=a_ττ компоненты ускорения направ-е по кас-й и наз-ся… касательной ускорения

V(dr/dt)=(V²/ρ)ň компонент ускорения, вектор направл по нормали, наз-ся нормалью ускорения

(V= , и над скоростью и нормалью везде стрелки!)

5.Кинематика твёрдого тела:

Поступательное движение твердого тела – это движение, при котором любая прямая, связанная с телом, при его движении остается параллельной своему начальному положению.

Примеры поступательного движения: движение педалей велосипеда относительно его рамы, движение поршней в цилиндрах двигателя внутреннего сгорания относительно цилиндров, движение кабин колеса обозрения относительно Земли (рисунок 1.1) и т.д.

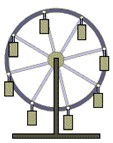
Рис. 1.1

Теорема. При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы.

Доказательство.

Если выбрать две точки твердого тела А и В (рисунок 1.2), то радиусы-векторы этих точек связаны соотношением

Траектория точки А – это кривая, которая задается функцией rA(t), а траектория точки B – это кривая, которая задается функцией rB(t). Траектория точки B получается переносом траектории точки A в пространстве вдоль вектора AB, который не меняет своей величины и направления во времени (AB = const). Следовательно, траектории всех точек твердого тела одинаковы.

Продифференцируем по времени выражение

Получаем

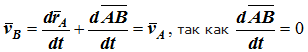
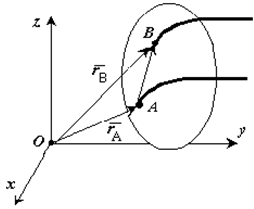
Рис. 1.2

Продифференцируем по времени скорость и получим выражение aB = aA. Следовательно, скорости и ускорения всех точек твердого тела одинаковы.

Для задания поступательного движения твердого тела достаточно задать движение одной из его точек:

Вращательное движение твердого тела

Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки (рисунок 1.3). Прямая, проходящая через эти точки, называется осью вращения. Положение тела определено, если задан угол φ между плоскостями П0 и П , одна из которых неподвижна, а другая жестко связана с телом.

φ=φ(t) – уравнение вращательного движения твердого тела.

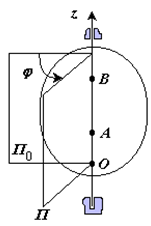
Рис. 1.3

За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z. Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.

Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω:

В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За одну минуту тело повернется на угол 2π⋅ n, где n – число оборотов в минуту (об/мин). Разделив этот угол на число секунд в минуте, получим

Вектор угловой скорости – это вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости

где k – единичный вектор оси вращения.

Угловое ускорение – мера изменения угловой скорости:

Вектор углового ускорения – производная вектора угловой скорости по времени (рис. 1.4)

генара - маленькие роторы, подвешенные без подшипников в магнитном поле.

Связь между линейной и угловой скоростями. Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть ее отличие от угловой скорости.

Мы уже отмечали, что при вращении твердого тела разные его точки имеют неодинаковые линейные скорости, но угловая скорость для всех точек одинакова.

Между линейной скоростью любой точки вращающегося тела и его угловой скоростью существует связь. Установим ее. Точка, лежащая на окружности радиусом R, за один оборот пройдет путь. Поскольку время одного оборота тела есть период T, то модуль линейной скорости точки можно найти так:

Так как , то

Из этой формулы видно, что, чем дальше расположена точка тела от оси вращения, тем больше ее линейная скорость.

Модуль ускорения точки тела, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности:

Следовательно,

Чем дальше расположена точка твердого тела от оси вращения, тем большее по модулю ускорение она имеет.

Плоское движение твёрдого тела:

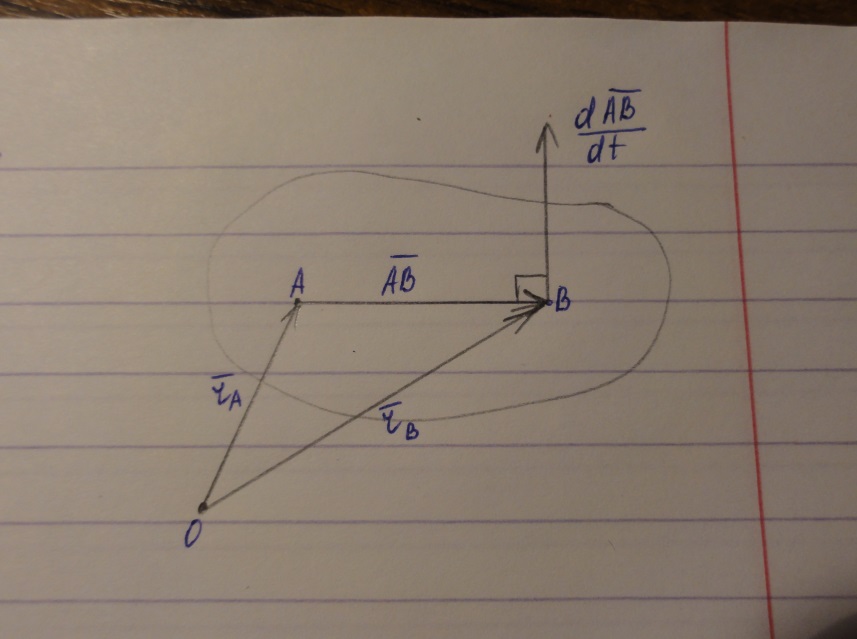
Плоским движением твёрдого тела называют такое движение, при котором любое плоское сечение тела в процессе движения остаётся в своей плоскости. Вектор, соединяющий две произвольные точки, является переменным вектором постоянного модуля. ā ┴ dā/dt

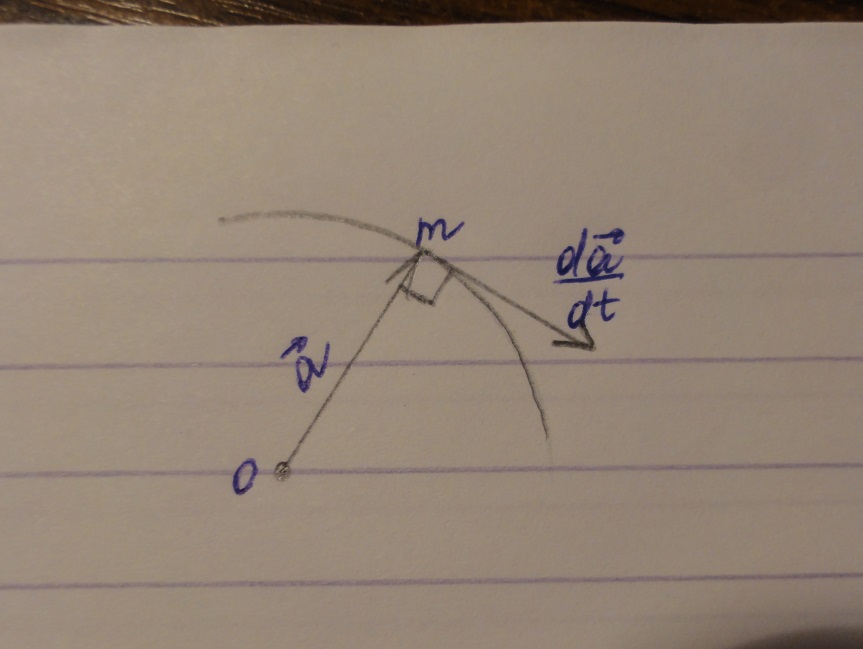
Скорости точек при плоском движении:

Пусть тело совершает плоское движение. Выберем 2 произвольные точки А,В и начало отсчёта. Положение точек определяется векторами.

AB – переменный вектор постоянного модуля rB = rA + AB (1) vB = drB/dt = d/dt (rA+rB) = drA/dt + dAB/dt vB = vA + dAB/dt (2) AB ┴ dAB/dt

Из того, что АВ является переменным вектором постоянного модуля, dAB/dt является скоростью движения точки В по окружности вокруг точки А.

Из формулы (2) следует, что плоское движение является суммой поступательного и вращательного движения.

Теорема о равенстве проекций скоростей:

В проекции скорости двух точек тела на прямую, соединяющую эти точки, равны.

Доказать: v_A * cos α = v_B * cos β

Доказательство: Пусть тело совершает плоское движение

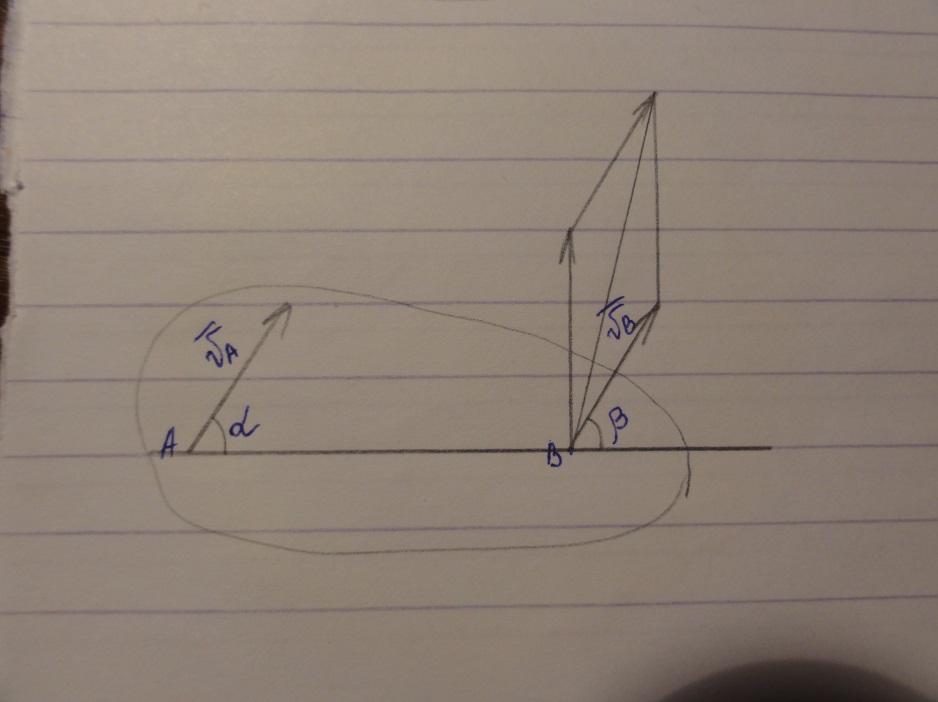
На основании формулы (2) найдём v_B:

BC = v_A * cos α

BC = v_B * cos β Из этого следует: v_A * cos α = v_B * cos β (3)

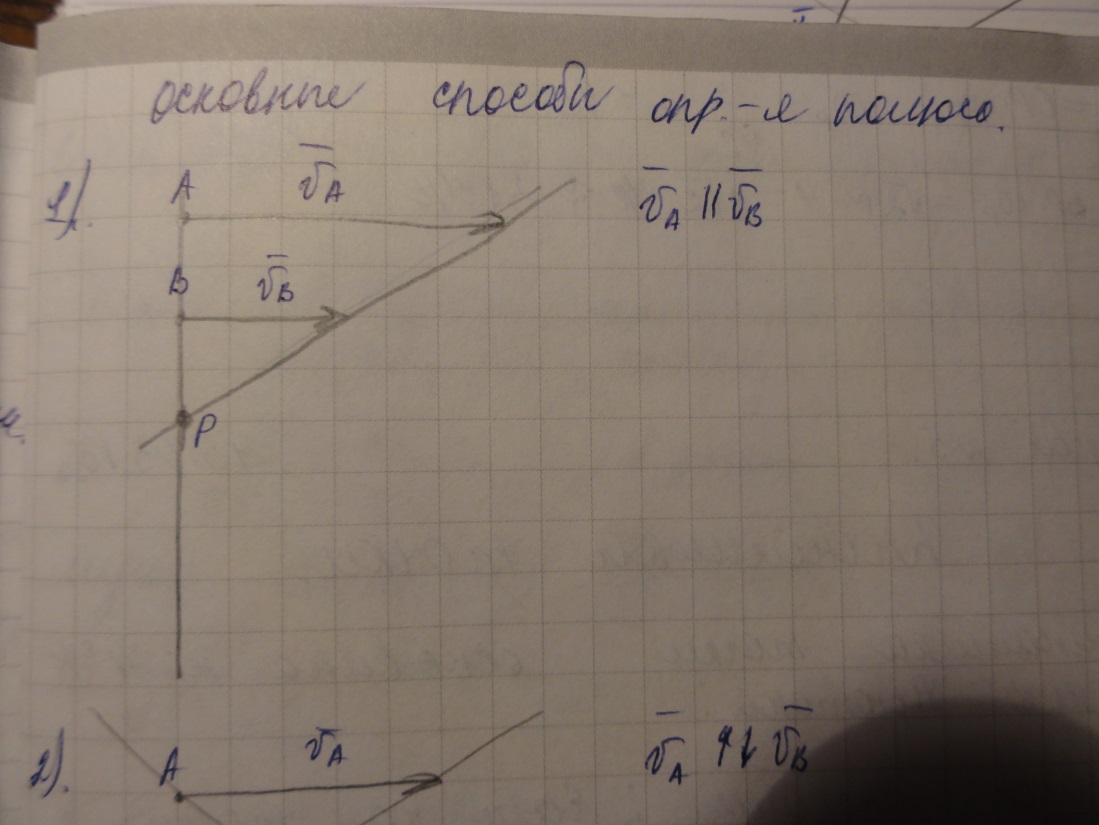
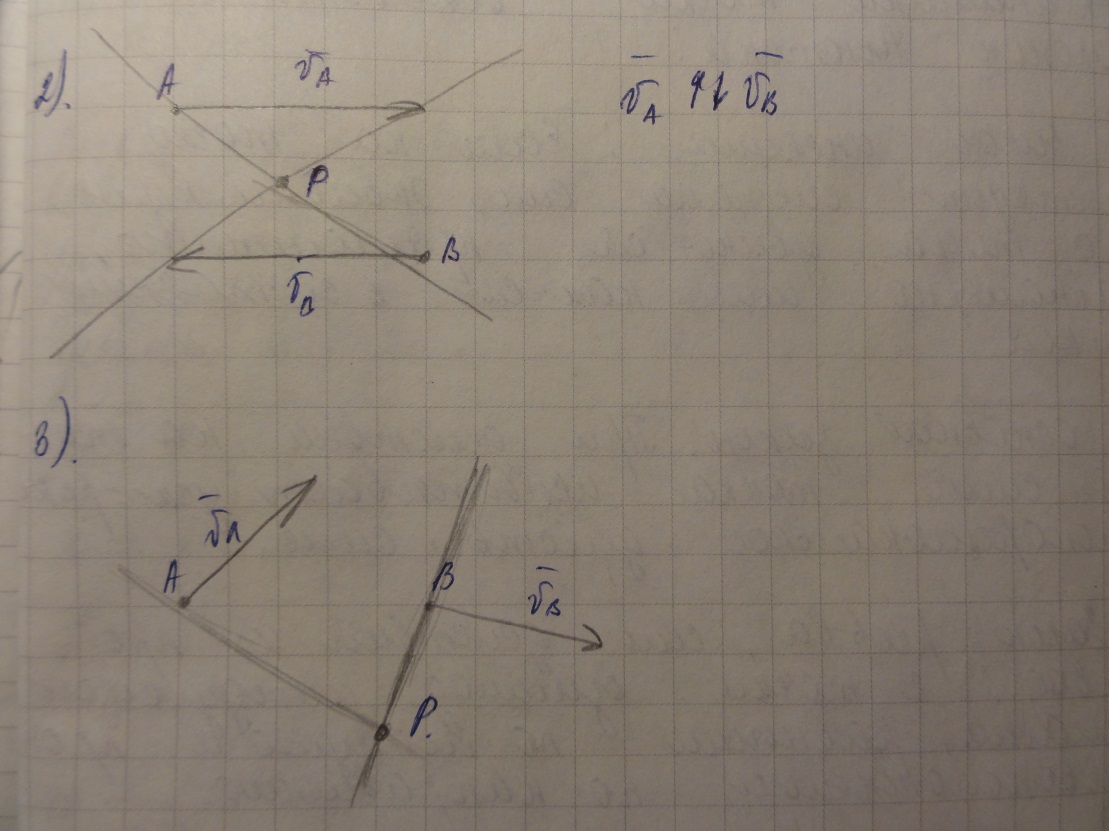
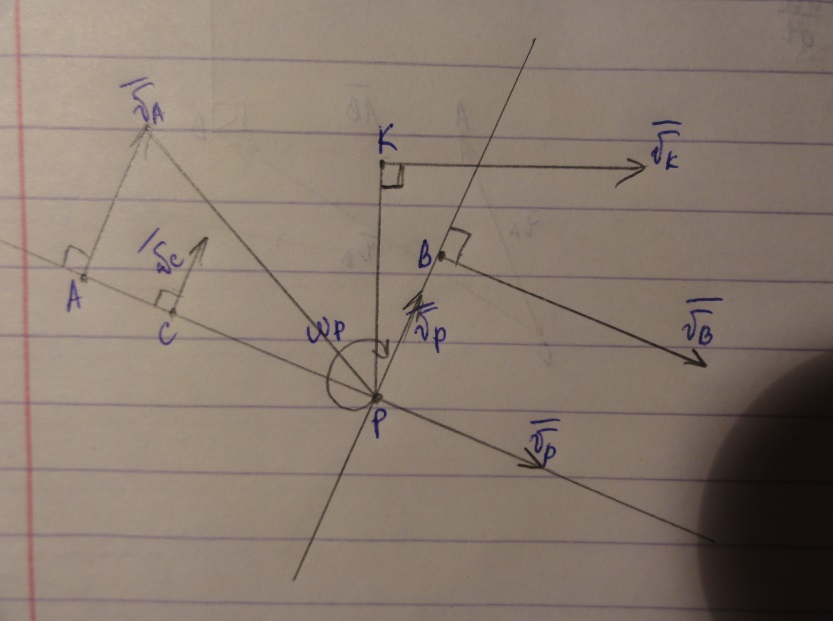
Мгновенный центр скоростей (полюс):

vp = 0 v = h * ω – формула Эллера vA = AP * ωp , vC = CP * ωp ωp = vA /AP , ωp = vC /CP Из этого следует: vA /AP = vC /CP

Пусть тело совершает плоское движение. Выберем две произвольные точки А,В и укажем направления скоростей этих точек v_A и v_B. Проведём прямые, проходящие через точки А и В и перпендикулярные скоростям v_A и v_B. Точку пересечения обозначим буквой р. На основании формулы (3) скорость точки р должна быть перпендикулярна прямым v_A и v_B одновременно, что может быть при условии v_p = 0. Так как обнаружена точка, где v = 0, можно сделать вывод, что плоскость движения является вращательным движением вокруг точки p с угловой скоростью ω_р. Следовательно, все точки тела движутся по окружности с радиусом, равным расстоянию от точки до полюса.