
- •Часть 1. Теоретическая механика.
- •1.Введение:
- •2.Статика:
- •3.Понятие вектора:
- •4.Кинематика точки.
- •1. Векторный способ задания движения точки.
- •2. Координатный способ задания движения точки.
- •3. Естественный способ задания движения точки.
- •5.Кинематика твёрдого тела:
- •6.Динамика точки:
- •Часть 2. Сопротивление материалов (см).
- •1.Введение:
- •2.Геометрические характеристики сечений:
- •3.Осевое растяжение-сжатие:
- •4.Кручение:
- •5.Изгиб:
Часть 1. Теоретическая механика.
1.Введение:
Теоретическая механика - наука об общих законах механического движения и взаимодействия материальных тел и механических систем
Механическим движением называется происходящее с течением времени изменение положения материальных тел относительно друг друга, а также изменение относительного положения частиц одного и того же материального шла, т. е. его деформация.
Основной задачей теоретической механики является изучение движения материальных тел под действием сил.
Курс теоретической механики принято делить на три основных раздела: статику, кинематику и динамику. В статике изучаются правила сложения сил и условия равновесия твердых тел. В кинематике изучаются движения тел лишь с геометрической стороны, вне зависимости от действующих на эти тела сил. И наконец, в динамике изучаются зависимости между движением материальных тел и действующими на них силами.
2.Статика:
Статика – это часть механики, которая изучает системы сил и условия равновесия материальных тел под действием сил.
Основные понятия статики.
Абсолютно твердые тела(АТТ)- это тело, в котором расстояние между 2-мя точками не меняется.
Под силой понимают эффект взаимодействия между телами. Сила является величиной векторной, следовательно, имеет точку приложения, направление, модуль, линию действия.
Свободное и несвободное тело. Тело несвязанное и нескрепленное с другими телами называется свободным. Тело скрепленное с другими телами называется несвободным. Всякое взаимодействие между телами называется связью. Связь характеризуется силой, которая называется силой реакции связи.
Система сил- совокупность сил, действующих на тело называется системой сил. Две системы эквивалентны, если оказываемое действия на тело одинаковы. Если система сил эквивалентна одной силе, то эта сила, называется равнодействующей. Если система сил эквивалентна 0, то такая система сил называется уравновешенной. Тело под действием уравновешенной системы сил находится в состоянии покоя.
Аксиомы статики.
Тело под действием 2-х сил находится в равновесии, тогда и только тогда, когда эти силы равны по модулю, противоположно направлении и действуют вдоль одной прямой.
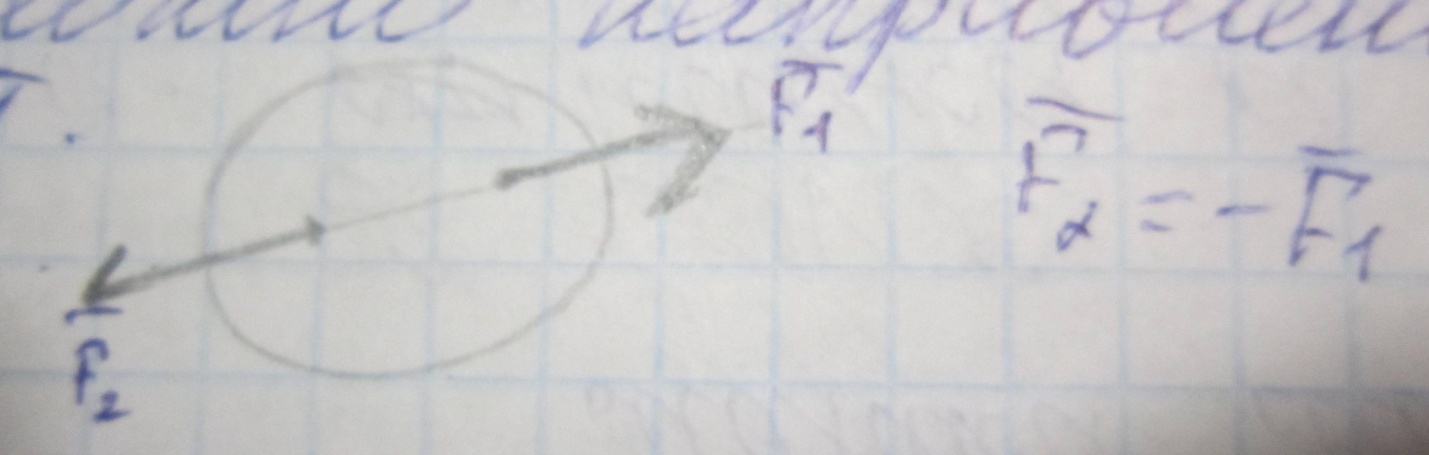
2.к телу всегда можно добавить или отнять уравновешенную систему сил.
Следствие к аксиоме №2. Сила является скользящим вектором, т.е. вектором, который можно свободно перемещать вдоль линии действия.
Доказательство: пусть на тело в точке А действует сила F

Покажем, что эту силу можно перенести в произвольную точку В. На основании аксиомы №2 в точке В можно приложить уравновешенную систему сил. На основании аксиомы №2 можно отнять уравновешенную систему сил. Что и требовалось доказать.
3.две силы приложенные к одной точке можно сложить по правилу параллелограмма.

4.Любое несвободное тело можно освободить, заменяя связь силой реакции связи.
Основные задачи статики:
Привидение заданной системы сил к простейшему виду.
Определение условий равновесия систем сил, действующих на твердое тело.
Сходящаяся система сил (ссс). Если линии действия сил пересекаются в одной точке, то такая система сил называется сходящейся.
Вывод условия равновесия системы сходящихся сил. Определим условия равновесия сходящейся системы сил.
Пусть на тело действует сходящаяся система сил . точка о – точка пересечения линий действия сил, т.к. силы являются скользящими векторами их можно перенести вдоль линии действия в точку О. теперь все силы приложены к одной точке и их можно попарно сложить( на основании аксиомы№3)
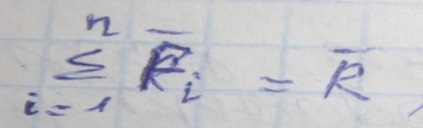 где
R-равнодействующая.
Если равнодействующая равна 0, то и
исходная система становится уравновешенной.
Таким образом, условие
где
R-равнодействующая.
Если равнодействующая равна 0, то и
исходная система становится уравновешенной.
Таким образом, условие
![]() -
является условием равновесия сходящейся
системы сил. Запишем это условие в
координатном виде.
-
является условием равновесия сходящейся
системы сил. Запишем это условие в
координатном виде.
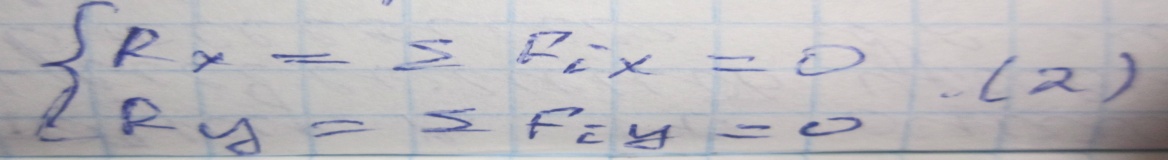 система
уравнений (2) является условием равновесия
сходящейся системы сил в координатном
виде.
система
уравнений (2) является условием равновесия
сходящейся системы сил в координатном
виде.
Разложение сил
Чтобы задача о разложении силы была определенной(т е имела бы одно решение), необходимо дополнительные указания(величина, направление одной из сопоставляющих или два направления)
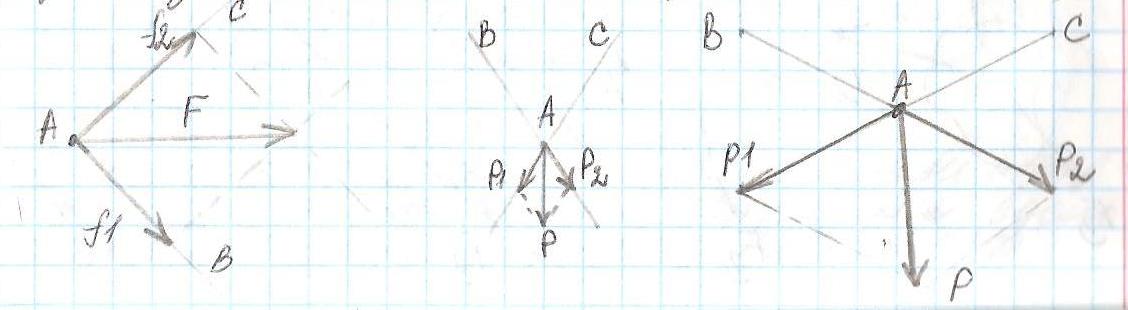
Проекция силы на ось- алгебраическая величина, равная произведению модуля силы на косинус угла между положительными направлением оси и вектором силы(т е это отрезок, откладываемый силой на соответсвующей оси)
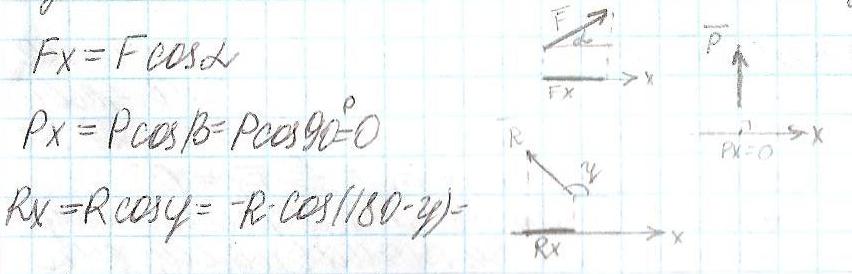
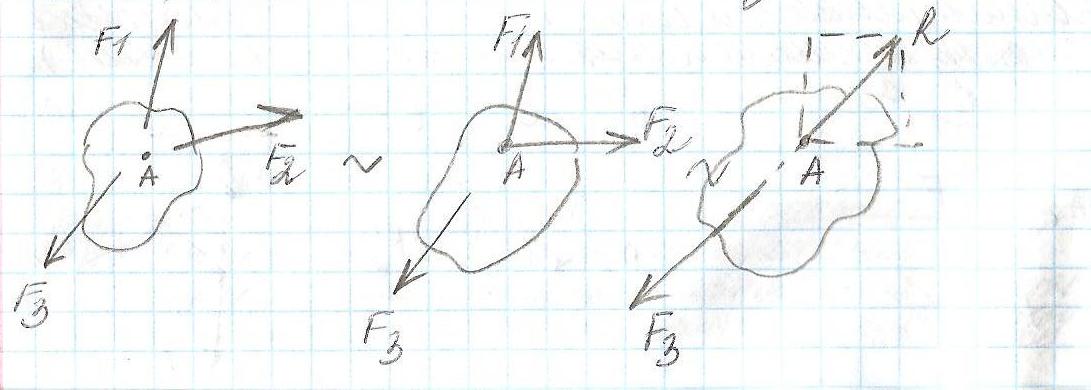
Теорема о трех силах
Если под действием 3 сил твердое тело находится в равновесии и линии действия двух сил пересекаются в одной точке, то все силы лежат в одной плоскости и их линии действия пересекаются в одной точке.
Пусть твердое тело действует система 3 сил F1 F2 F3, причем линии действия первых двух пересекаются в т А(а);
Силы F1 F2 переносим в т А(б). Сложим эти силы заменив их одной силой, равной R=F1+F2
R и F3 имеют общую линию действия. Исходные 3 силы лежат в одной плоскости, а линии действия сил пересекаются в одной точке.
Теорема о трех силах позволяет в рядах задач найти линию действия неизвестной силы, приложенной к твердому телу
Связь
Тело, которое может совершать из данного положения любые перемещения в пространстве называется свободным.
Тело, перемещениям которого препятствует какие нибудь другие скрепленные или соприкасающиеся с ним тела, называются несвободным.
Все то, что ограничивает перемещение данного тела, называют связью.
Принцип освобождаемости: несвободное твердое тело можно рассматривать как свободное, если его мысленно освободить от связей , заместив их действия реакциями
Реакция связи- сила, с которой данная связь действует на тело, препятствующая тем или иным его перемещениям.
Реакция связи направлена в сторону противоположную той, куда связь не дает перемещаться телу.
Основные типы связи:
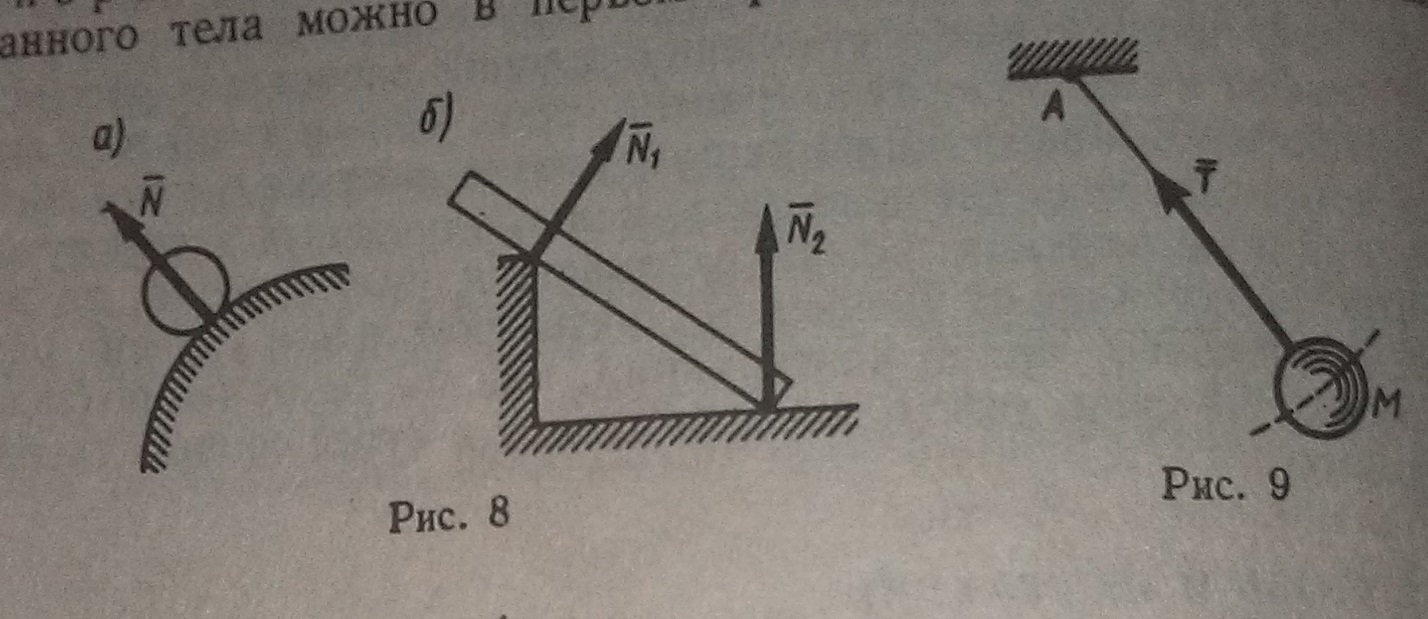
Гладкая поверхность. Сила гладкой связи перпендикулярна поверхности. Рис(8)
Гибкая не растяжимая нить. Реакций нити всегда направлена вдоль нити.
Неподвижный шарнир. В случае неподвижных шарниров направление реакций заранее не известно и он определяется в процессе решения задач.
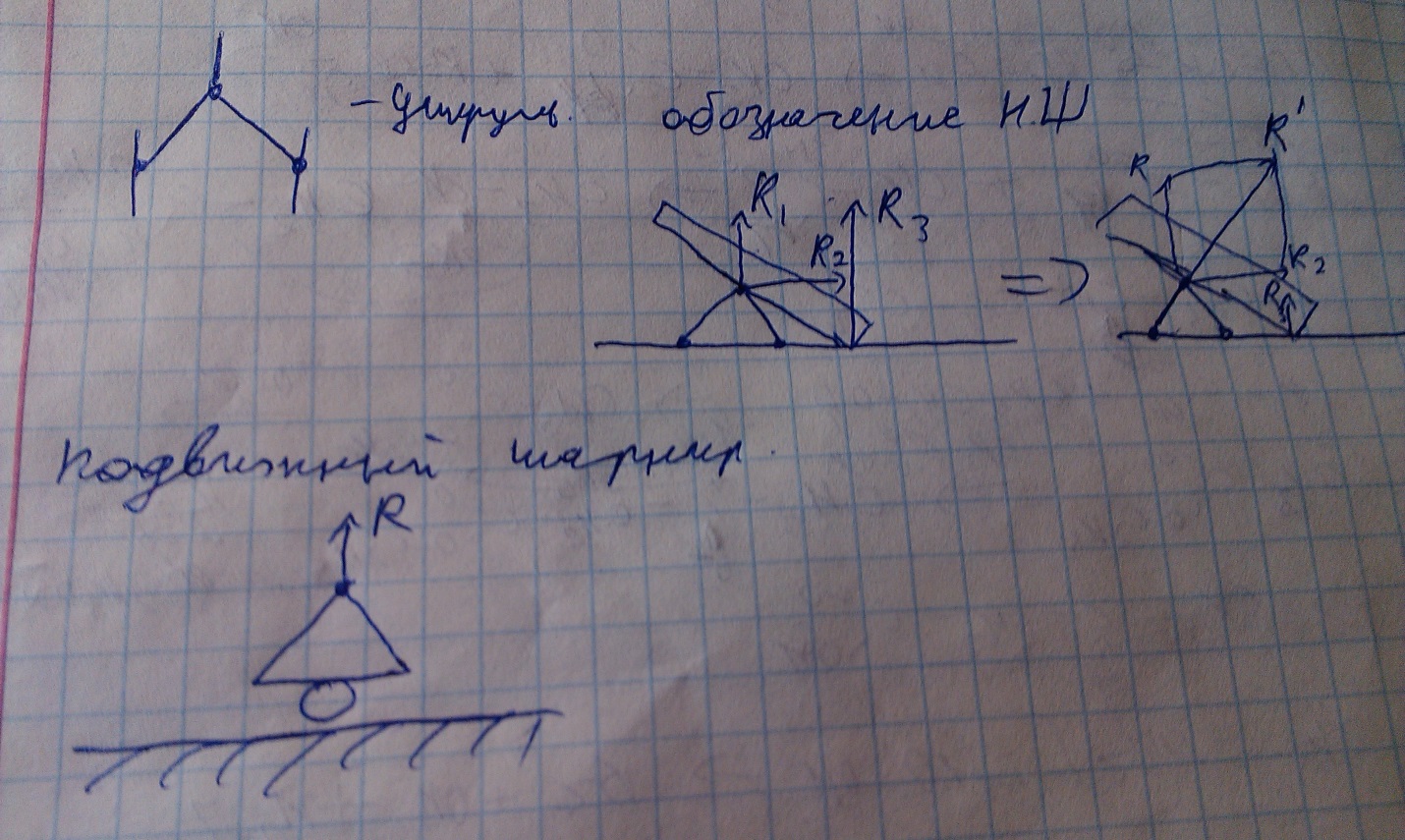
Подвижный шарнир. Каток.
Для подвижного шарнира реакция в горизонтальном направлений нет, поэтому реакция только в направлений перпендикулярном поверхности.
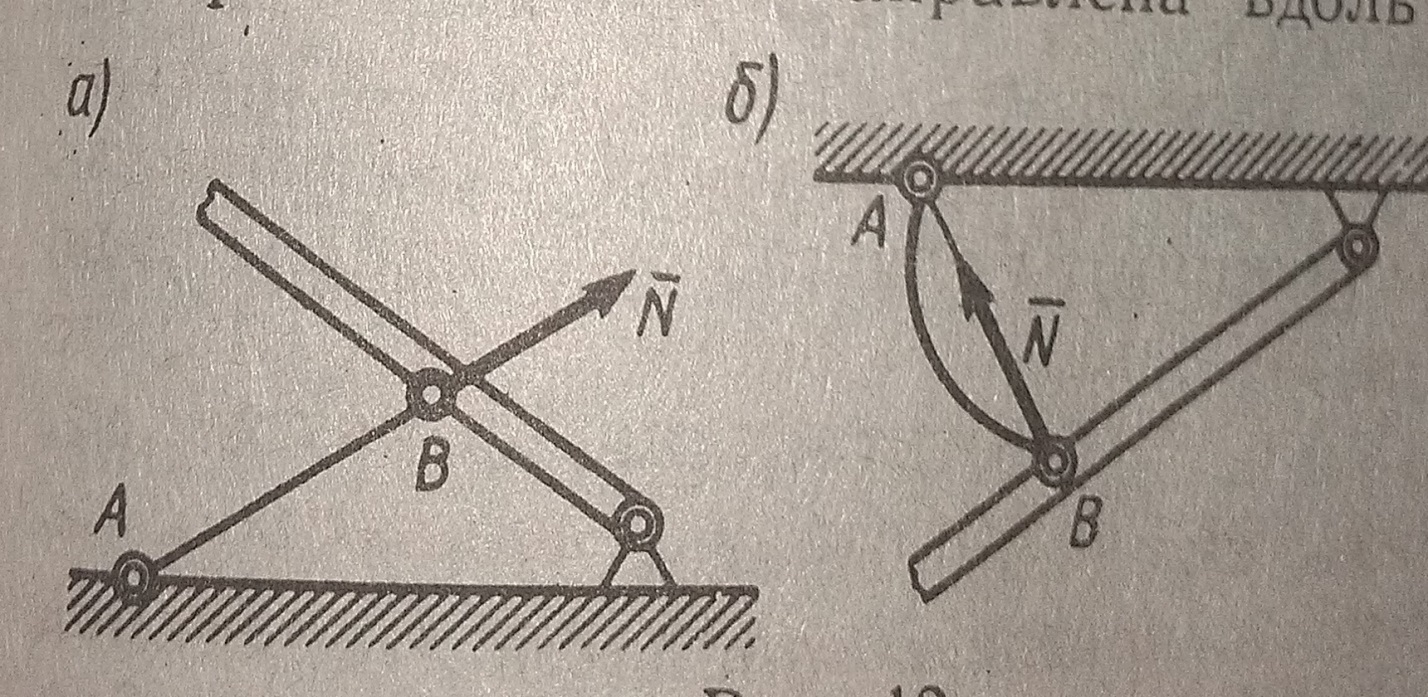
Невесомый недеформируемый стержень с шарнирами на концах. Реакция такого стержня всегда направлена вдоль стержня в сторону противодействия деформаций.
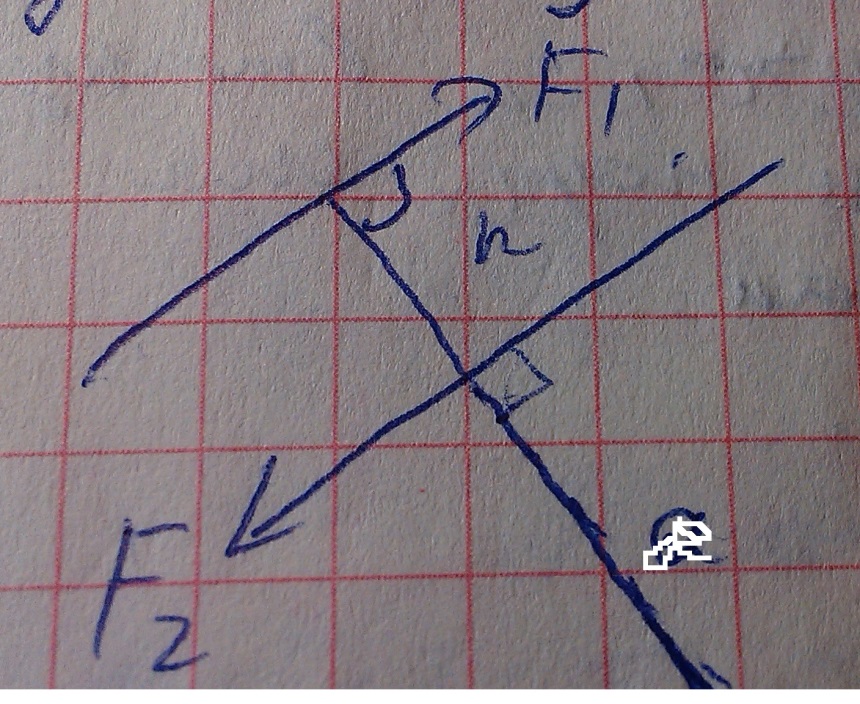
Момент силы относительно точки.
Пусть
сила F
приложена в точке А выделим начало
отсчёта точки О, тогда положение точки
А определяется вектором rугол
между векторами α.
 называется
моментом силыF
относительно точки О
называется
моментом силыF
относительно точки О
Определим модуль Mo(F)
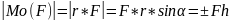
Проведём из точки о перпендикуляр на F
Отсюда
r*sinα=
Момент силы характеризует поворот тела вокруг выбранного центраО. Момент силы =0 если h=0 тоесть линия действия силы проходит через центр О.
h-плечо силы, поворот против часовой стрелки с плюсом(+)
поворот по часовой с минусом(-)
Tеорема Вариньона. Положение ядра.
Пусть
на тело действуют система сходящихся
сил в этом случае эта система сходится
к равнодействующей R=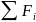 (1)
(1)
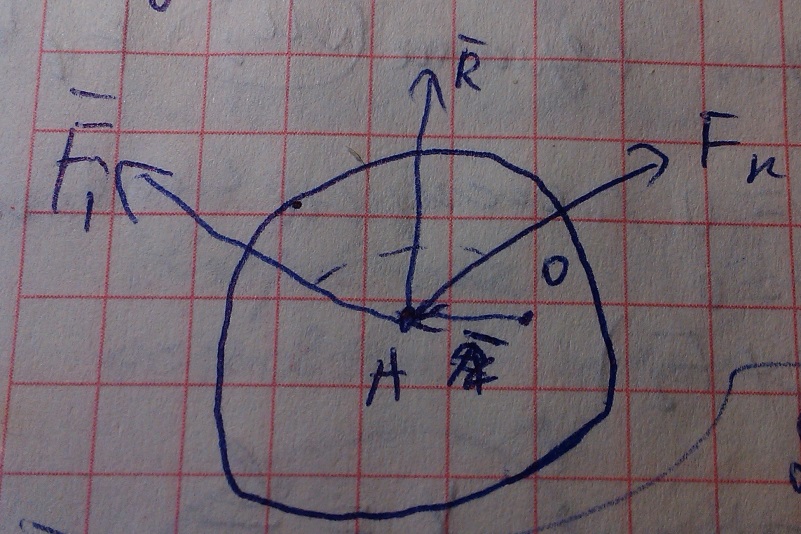
 (2)
(2)
Доказательство:
умножем уравнение 1 векторно на вектор
r
получим
r*R=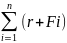 ==>
==>
M0(R)=M0(Fi)
Пара сил. Вычисление момента пары сил.
Система
двухравных по модулю и противоположенными
по направлению силами называют парой
сил. Растояние между этими силами
называется плечо силы.
Пара не имеет равнодействующую, Пара сил характеризуется моментом пары и приводит к повороту тела, тоест пара сил характеризуется моментом.
Момент пары равен сумме моментов сил составляющих пару относительно произвольного центра О.
Теорема.
Момент пары не зависит от выбора центра
О
Доказательство: выберем произвольный центр. Пусть на тело действует пара силF1=F2=F3
M(П)=- -F(a+b)+F*a=-Fh.
-F(a+b)+F*a=-Fh.
Из теоремы следует что М. пары является свободным вектором тоесть его можно переносить в любое место плоскости действия.
Плоская система сил
Система сил, действующая на плоскости, линии действия которых не пересекаются в одной точке, называют плоской системой сил.
Теорема о параллельном переносе (Основная теорема статики)теорема Поансо
Пусть к телу в точка А приложена сила F. Выберем произвольную точку О. Проведем через нее прямую паралелльную силе F и приложим к этой точке СС ̴ 0

Приведение ПСС к единому центру.
Пусть на тело действует ПСС. Выберем центр О. На основании основной теоремы статики все эти силы можно параллельно перенести в точку О, добавляя при этом пары сил с соответствующими моментами

Теперь все силы приложены к одной точке и их можно сложить
Вектора моментов, являющиеся свободными векторами можно перенести в одну точку и сложить

Вывод условий равновесия произвольной ПСС
Из формулы (1) следует, что ПСС сводится к двум векторам. Если главный вектор и главный момент равны 0, то ПСС становится уравновешенной, а тело находится в состоянии покоя.
Запишем систему уравнений (2) в координатном виде:
