2. Для построения фронтального следа n прямой нужно из точки пересечения горизонтальной проекции её с осью 0x восстановить перпендикуляр до пересечения с фронтальной проекцией прямой.

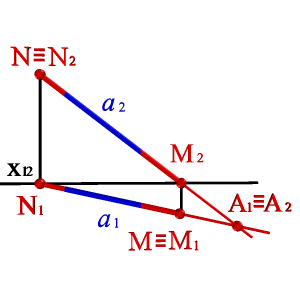
		С помощью этих правил найдены на эпюре следы прямой а (рис.27) . Здесь же показаны совпавшие проекции точки А, принадлежащей рассматриваемой прямой. Особенность этой точки в том, что она равноудалена от плоскостей проекций, то есть находятся в биссекторной плоскости 2бис. Следы прямой, являются точками, в которых прямая переходит из одного октанта в другой, позволяют отмечать её видимость. Видимой частью прямой будет та, которая расположена в пределах первого октанта.

Вопрос 15 Определение натуральной величины отрезка. Способ треугольника

Отрезок [AB] – отрезок прямой общего положения. Ни одна из проекций отрезка не равна его натуральной величине.

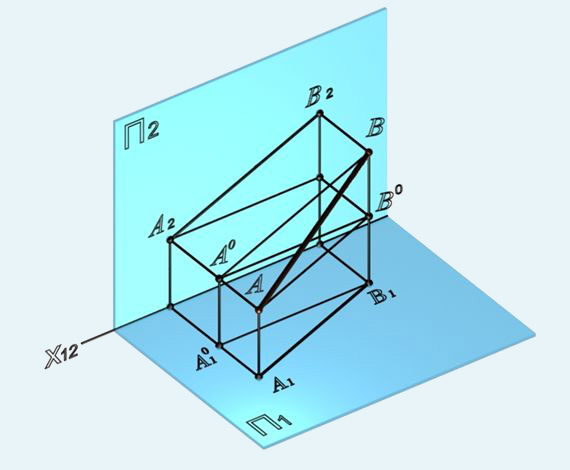
Рис. 31. Определение натуральной величины отрезка способом треугольника

На рис. 31 A₁ABB₁ – прямоугольная трапеция, наклонной стороной которой является отрезок [AB] , высотой – его горизонтальная проекция [A₁B₁] , основаниями – горизонтально-проецирующие прямые (AA₁) и (BB₁) .

Если провести прямую (AB⁰)∥(A₁B₁) , то от трапеции A₁ABB₁ отсекается прямоугольный треугольник ABB⁰) с гипотенузой [AB], один катет которого [AB⁰]=[A₁B₁] , другой BB⁰– равен разности высот точек A и B.

На комплексном чертеже (рис. 32, а) прямоугольный треугольник строится непосредственно при горизонтальной проекции отрезка: ΔA₁B₁B'=ΔABB⁰ . Одним катетом прямоугольного треугольника является горизонтальная проекция [A₁B₁] , вторым – разность высот точек A и B (отрезок [BB⁰]=[B₁B'] ), гипотенуза [A₁B'] и будет равна натуральной величине отрезка [AB].

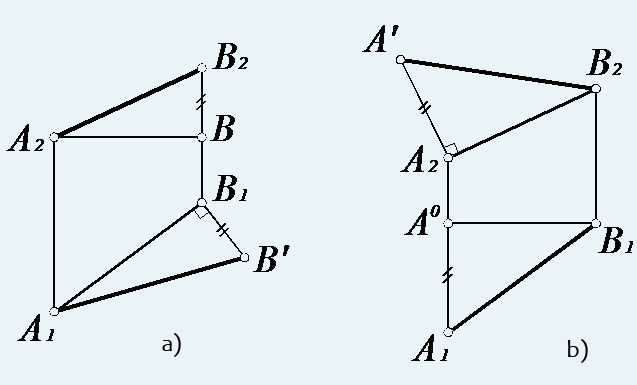
Рис. 32. Определение натуральной величины отрезка: а – на горизонтальной проекции; б – на фронтальной проекции

Аналогичные построения возможны и на фронтальной проекции (рис. 32, б), тогда одним катетом прямоугольного треугольника является фронтальная проекция[A₂B₂], а вторым – разность глубин точек A и B (отрезок [A₂A']=[ A₁A⁰]), гипотенуза [B₂A'] будет равна натуральной величине отрезка [AB].

Таким образом, можно сформулировать общее правило:

Натуральная величина отрезка прямой определяется гипотенузой прямоугольного треугольника, одним катетом которого является одна из проекций отрезка, а вторым – разность расстояний концов другой проекции отрезка относительно друг друга.

Вопрос 16

ВЗАИМНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ

Прямые в пространстве могут: совпадать;

пересекаться; быть параллельными; скрещиваться

Две прямые являются совпадающими, если на видах спереди 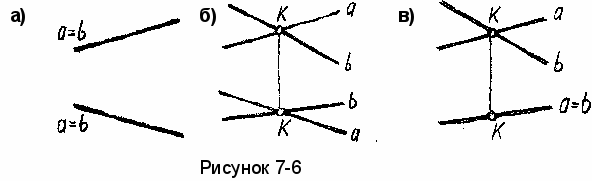 и сверху они сливаются (рисунок 7-6а). Пересекающиеся прямые имеют общую точку – К, изображение которой на видах спереди и сверху расположены на одной линии связи (рисунок 7-6б). Проекции пересекающихся прямых на одном из видов могут совпадать (рисунок 7-6в), такие прямые называются конкурирующими. Так как здесь они совпадают на виде сверху (на горизонтальной проекции), то в данном случае это горизонтально - конкурирующие прямые. 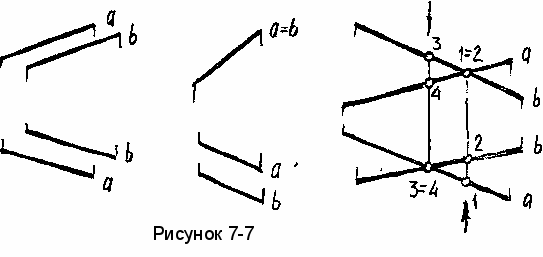Если прямые а и Ь параллельны, то на основании свойства параллельного проецирования их одноименные проекции будут параллельны (рисунок 7-7а). Проекции параллельных прямых на одном из видов могут совпадать, в этом случае прямые называютсяконкурирующими параллельными прямыми. На рисунке 7-7б изображены фронтально-конкурирующие прямые а и Ь, т.к. их изображения совпадают на виде спереди. а) б) в) В заимное положение конкурирующих прямых определяют по тому виду, на котором их изображенияне совпадают. Скрещивающиеся прямые - это такие прямые, которые не пересекаются и не параллельны друг другу (рисунок 7-7в). Если параллельные и пересекающиеся прямые всегда лежат в одной плоскости (задают плоскость), то скрещивающиеся прямые в одной плоскости не лежат. Кажущиеся точки пересечения прямых 1 и 2, 3 и 4 будут попарно конкурирующими; у них совпадает только одна из одноименных проекций: т.т.1 и 2 - конкурируют на виде спереди, т.т.3 и 4 - конкурируют на виде сверху. Итак, - взаимное положение прямых общего положения определяется по двум видам заданных прямых.