Вопрос 10.

Прямая общего положения - это прямая не параллельная и не перпендикулярная ни одной из плоскостей проекций.

Отрезок [AB] определяющий прямую l занимает произвольное положение по отношению к плоскостям проекций (углы наклона прямой l к плоскостям H, V, и W произвольные - отличные от 0 и 90 град.). Такая прямая есть прямая общего положения.

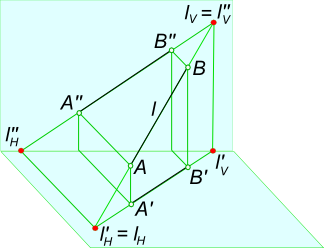
Прямая общего положения

Прямая общего положения пересекает все три плоскости проекций. Точку пересечения (встречи) прямой с плоскостью проекции называют следом прямой.

Прямая общего положения

В зависимости от того, с какой плоскостью проекции происходит встреча прямой l, следы обозначают и называют: l _H - горизонтальный след прямой l; l _V - фронтальный след прямой l; l _W - профильный след прямой l.

Вопрос 11. Прямая параллельная плоскости.

Прямая параллельна плоскости, когда она параллельна прямой, лежащей в этой плоскости. Если требуется провести прямую параллельно данной плоскости, то сначала надо провести в плоскости какую-либо прямую, а затем провести прямую, ей параллельную, которая будет параллельна данной плоскости. В плоскости можно провести неограниченное число прямых линий, следовательно, можно провести неограниченное количество и прямых, параллельных плоскости.

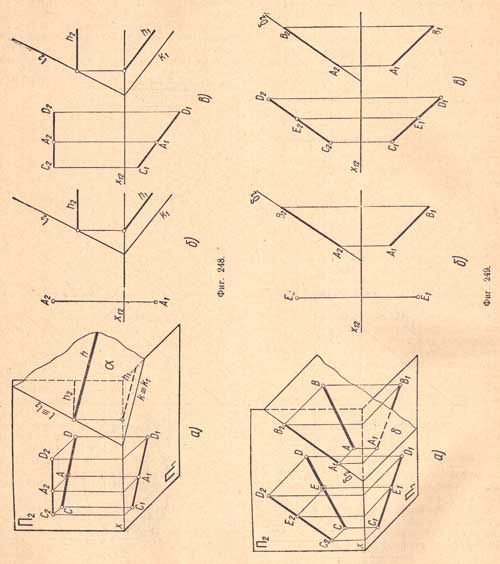
Пример 1. Через данную точку A (A₁ A₂) требуется провести прямую, параллельную плоскости а общего положения, заданной следами (фиг.248,а). 1. Проведем в плоскости а произвольную прямую, например горизонталь h(h₁, h₂) (фиг.248,б). 2. Проведем через точку А₁ прямую C₁D₁ параллельную прямой h₁ а через точку А₂ - C₂D₂, параллельную h₂ (фиг.248,в). Прямая CD (C₁D₁ и С₂D₂) параллельна плоскости а, так как параллельна прямой (горизонтали) h этой плоскости. Пример 2. Дана фронтально - проектирующая плоскость δ ее фронтальной проекцией и точка Е (Е₁ Е₂) вне плоскости. Требуется провести через данную точку Е прямую параллельно плоскости δ (фиг.249,а). 1. Проводим в плоскости δ какую - либо прямую, например прямую АВ(A₁B₁ A₂B₂) общего положения (фиг.249,б). 2. Проводим через данную точку Е (E₁ E₂) прямую CD (C₁D₁, C₂D₂) параллельно прямой АВ (фиг.249,в). Проведенная прямая CD параллельна данной плоскости δ, так как она параллельна прямой, лежащей в этой плоскости.

Вопрос 12.

ПРЯМАЯ, ПЕРПЕНДИКУЛЯРНАЯ ПЛОСКОСТИ

Большое значение для задач начертательной геометрии имеет частный случай пересечения прямой и плоскости, когда прямая перпендикулярна плоскости.

Докажем следующую теорему о перпендикуляре к плоскости: Если прямая перпендикулярна плоскости, то горизонтальная проекция этой прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция – фронтальной проекции фронтали плоскости.

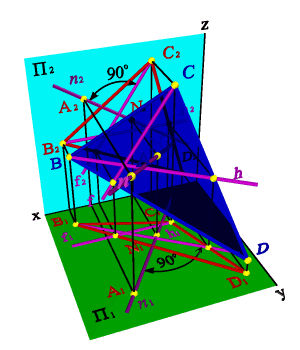
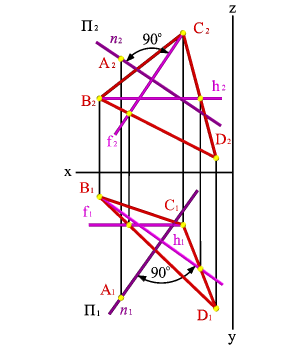
Пусть прямая n, перпендикулярная плоскости, пересекает плоскость BCD в точке N, тогда по условию n перпендикулярна любой прямой плоскости. Проведем в плоскости BCD горизонталь h, а на основании теоремы о проецировании прямого угла можно утверждать, что на горизонтальную плоскость проекций они проецируются под прямым углом, т.е. n₁h₁. Аналогично для фронтали – fn   f₂ n₂.

Справедлива и обратная теорема: Если проекции прямой перпендикулярны одноименным проекциям соответствующих главных линий плоскости (горизонтали и фронтали), то такая прямая перпендикулярна плоскости.

Доказательство следует из теоремы  о проецировании прямого угла.

Исходя из рассмотренных теорем, можно решить задачу о построении перпендикуляра к плоскости из точки А (рис.61).

Задача. Дано: плоскость ВСD и точка А.

Требуется построить прямую линию n проходящую через точку А и перпендикулярную плоскости ВСD.

В плоскости ВСD построим фронталь f и горизонталь h. В горизонтальной плоскости проекций проведем через точку А₁ прямую n₁перпендикулярно горизонтальной проекции горизонтали h₁, а на фронтальной плоскости проекций через точку А₂ прямую n₂ перпендикулярно фронтальной проекции фронтали f₂, согласно, теореме о перпендикуляре к плоскости, полученная прямая n будет перпендикулярна плоскости ВСD.