
- •Математика
- •Введение
- •Элементы теории множеств и математической логики
- •1 Элементы теории множеств и математической логики
- •Множества и операции над ними
- •1.2. Законы алгебры множеств
- •1.3. Бинарные отношения и их свойства
- •Решение
- •1.4. Высказывания и операции над ними
- •1.5.Формулы логики высказываний. Равносильность формул
- •Решение
- •Предикаты и кванторы
- •Решение
- •Оглавление
- •1.Элементы теории множеств и математической логики 4
- •1.3 Бинарные отношения и их свойства 12
Решение
Найдем множества истинности данных предикатов:
![]() ;
;
![]() ;
;
![]() .
.
Видим,
что
![]() .
Учтем этот факт при изображении данных
множеств с помощью кругов Эйлера-Венна.
.
Учтем этот факт при изображении данных
множеств с помощью кругов Эйлера-Венна.
а) Найдем область истинности предиката .
![]()

б)
Для построения области истинности
предиката
![]() упростим его:
упростим его:
![]() .
.
Тогда
![]()

Области
истинности предикатов
![]() и
показаны на рисунках штриховкой.
и
показаны на рисунках штриховкой.
Элементы линейной алгебры и аналитической геометрии
Теоретические вопросы
Виды матриц. Операции над матрицами: сложение, умножение на число, умножение матриц.
Определители второго и третьего порядков. Свойства определителей.
Миноры и алгебраические дополнения. Обратная матрица.
Системы линейных уравнений. Теорема Крамера.
Матричный способ решения систем линейных уравнений.
Векторы. Линейные операции над ними.
Скалярное произведение двух векторов и его свойства.
Векторное произведение двух векторов и его свойства.
Смешанное произведение трёх векторов и его свойства.
Прямая на плоскости. Взаимное расположение прямых.
Прямая и плоскость в пространстве. Взаимное расположение плоскостей, прямой и плоскости в пространстве.
Литература
Лунгу, К.Н. Сборник задач по высшей математике. 1курс. М.: Айрис-пресс, 2004.– 576с.
Письменный, Д.Т. Конспект лекций по математике. Ч.1. М.: Айрис-пресс, 2004.– 288с.
Турецкий, В.Я. Математика и информатика. – М: ИНФРА-М, 2005. – 560с.
Высшая математика: метод. указания и контрольные задания для студентов заочного отделения.Ч.1/авт.сост. О.Н.Барсов; НовГУ имени Ярослава Мудрого. – Великий Новгород, 2009.– 75с.
Задачи для контрольных работ
Контрольная работа 1
Элементы теории множеств и математической логики:
Задание 1. Даны множества и . Изобразить и записать с указанием характеристического свойства результат каждой операции:
а)
;
б)
;
в)
;
г)
![]() ;
д)
;
е)
;
ж)
;
д)
;
е)
;
ж)
![]() ;
з)
;
з)
![]() .
.
-
1.

 .
.2.

 .
.3.

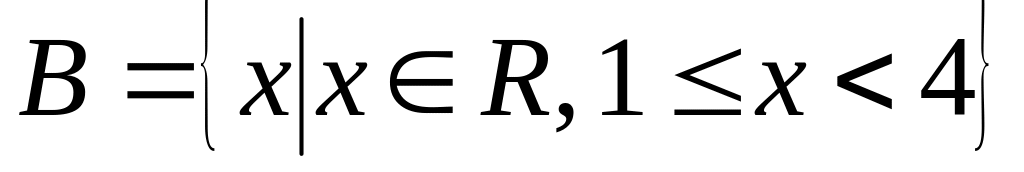 .
.4.

 .
.5.


6.


7.


8.


9.


10.


Задание 2. На диаграммах Эйлера-Венна изобразить результат операций, предварительно указав порядок действий в формуле.
-
1.

2.
 .
.3.

4.

5.

6.

7.

8.

9.

10.

Задание 3. Упростить выражения, используя законы алгебры множеств.
1.
 .
.2.
 .
.3.
 .
.4.
 .
.5.
 .
.6.
 .
.7.
 .
.8.
 .
.9.
 .
.10.
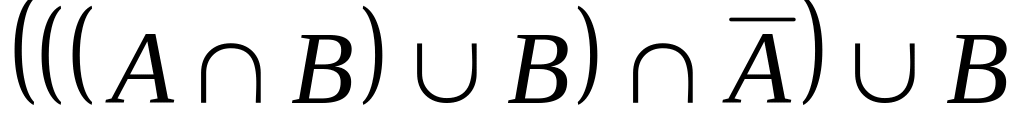 .
.
Задание 4. Упростить формулы логики двумя способами: а) используя таблицы истинности; б) с помощью равносильных преобразований.
-
1.а)
 ;
б)
;
б)
 .
.2. а)
 ;
б)
;
б)
 .
.3.а)
 ;
б)
;
б)
 .
.4. а)
 ;
б)
;
б)
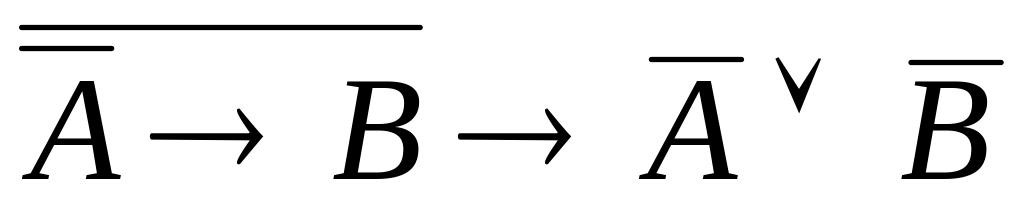 .
.5. а)
 ;
б)
;
б)
 .
.6. а)
 ;
б)
;
б)
 .
.7. а)
 ;
б)
;
б)
 .
.8. а)
 ;
б)
;
б)
 .
.9. а)
 ;
б)
;
б)
 .
.10. а)
 ;
б)
;
б)
 .
.
Задание
5.
На множестве
![]() заданы предикаты:
– «
–
чётное число»,
– «
делится
нацело на 3»,
– «
–
число простое»,
заданы предикаты:
– «
–
чётное число»,
– «
делится
нацело на 3»,
– «
–
число простое»,
![]() – «
не делится на 5». Найти и изобразить при
помощи диаграмм Эйлера-Венна множества
истинности предикатов
,
,
,
и следующих сложных предикатов:
– «
не делится на 5». Найти и изобразить при
помощи диаграмм Эйлера-Венна множества
истинности предикатов
,
,
,
и следующих сложных предикатов:
-
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
а)
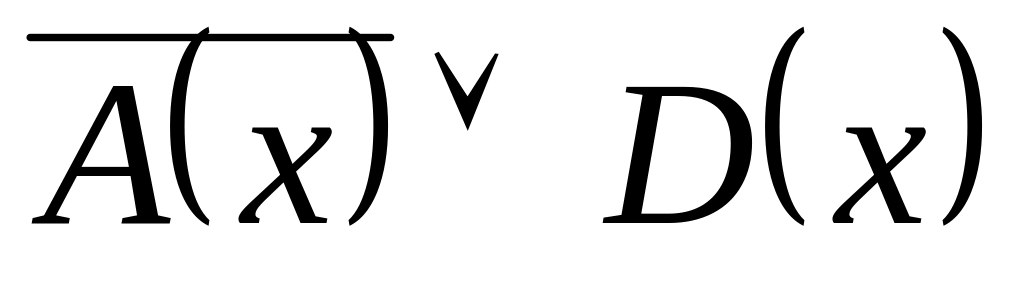 ;
б)
;
б)
 ;
в)
;
в)
 .
.
а)
 ;
б)
;
б)
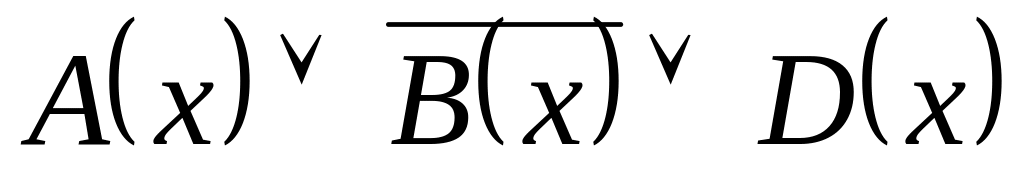 ;
в)
;
в)
 .
.
а)
 ;
б)
;
б)
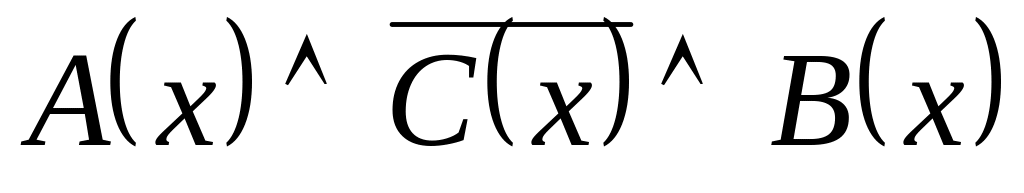 ;
в)
;
в)
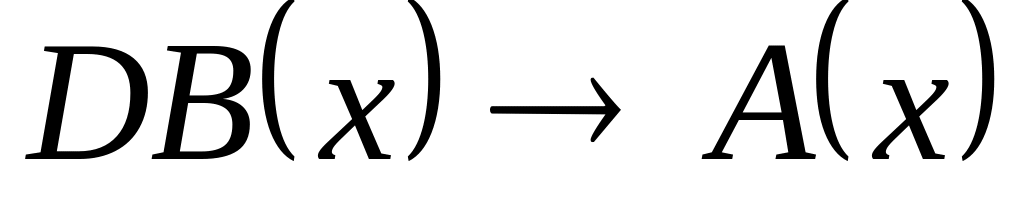 .
.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
Задание
6.
На множестве
бинарное отношение
![]() задано характеристическим свойством.
Представить отношение
другими возможными способами. Выяснить
какими свойствами оно обладает.
задано характеристическим свойством.
Представить отношение
другими возможными способами. Выяснить
какими свойствами оно обладает.
1.
|
|
|
2.
|
|
|
3.
|
|
|
4.
|
|
|
5.
|
|
|
6. |
|
|
7.
|
|
|
8.
|
делится на 3; |
|
9. |
|
|
10.
|
|
|
Контрольная работа 2
Элементы линейной алгебры и аналитической геометрии
Задание
1.
Найти значение матричного многочлена
на
![]() .
.
-
1.
 .
.2.
 .
.3.
 .
.4.
 .
.5.
 .
.6.
 .
.7.
 .
.8.
 .
.9.
 .
.10.
 .
.
Задание 2. Решить систему линейных уравнений двумя способами: 1) с помощью формул Крамера; 2) средствами матричного исчисления.
-
1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

Задание
3.
Даны векторы
![]() Найти:
1) линейную комбинацию
Найти:
1) линейную комбинацию
![]() векторов; 2) скалярное произведение
векторов; 2) скалярное произведение
![]() и
;
3) угол между векторами
и
;
3) угол между векторами
![]() и
и
![]() ;
4) площадь параллелограмма, построенного
на векторах
и
;
4) площадь параллелограмма, построенного
на векторах
и
![]() ;
5) объём параллелепипеда, построенного
на векторах
;
5) объём параллелепипеда, построенного
на векторах
-
1.
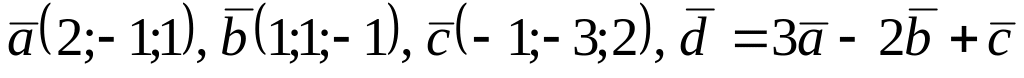 .
.2.
 .
.3.
 .
.4.
 .
.5.
 .
.6.
 .
.7.
 .
.8.
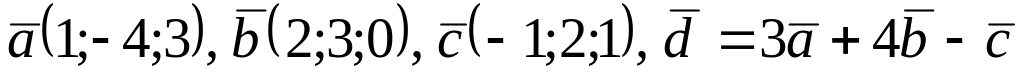 .
.9.
 .
.10.
 .
.
Задание
4.
Даны вершины треугольника
![]() Найти: 1) длину стороны
Найти: 1) длину стороны
![]() ;
2) уравнение прямой
;
3) уравнение медианы
;
2) уравнение прямой
;
3) уравнение медианы
![]() ;
4) уравнение высоты
;
4) уравнение высоты
![]() ;
5) площадь треугольника
;
5) площадь треугольника
![]() ;
6) длину высоты
;
7) уравнение окружности, для которой
высота
является диаметром.
;
6) длину высоты
;
7) уравнение окружности, для которой
высота
является диаметром.
-
1.

2.

3.
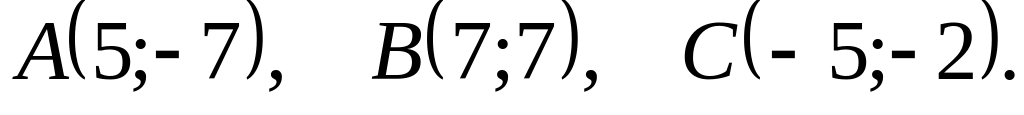
4.
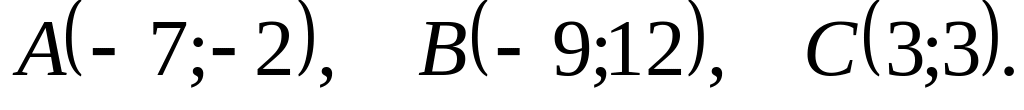
5.

6.
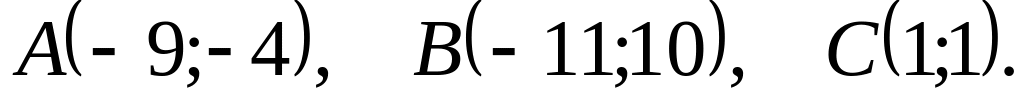
7.

8.

9.

10.

Задание
5.
Даны точки
![]() и
и
![]() .
Доказать, что они не лежат в одной
плоскости. Найти: 1) уравнение плоскости
;
2) уравнение плоскости, параллельной
и проходящей через точку
;
3) уравнение прямой, проходящей через
точку
и
перпендикулярной
;
4) длину высоты, опущенной из
на грань
;
5) объём пирамиды
.
Доказать, что они не лежат в одной
плоскости. Найти: 1) уравнение плоскости
;
2) уравнение плоскости, параллельной
и проходящей через точку
;
3) уравнение прямой, проходящей через
точку
и
перпендикулярной
;
4) длину высоты, опущенной из
на грань
;
5) объём пирамиды
![]() .
.
-
1.

2.

3.

4.
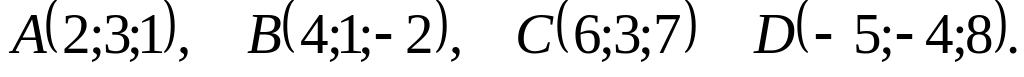
5.

6.

7.

8.

9.

10.

