7.1.2. Операции над нечёткими множествами.

Над нечеткими множествами выполняются те же операции, что и над обычными множествами.

Пусть:

U=(u₁, u₂, u₃, u₄, u₅, u₆, u₇)

А = {(0,6/u₁); (0,4/u₂); (0,3/u₃); (0,8/u₄); (0,5/u₅); (1/u₆); (0,6/u₇)}

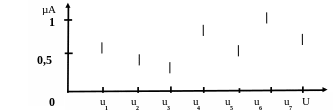
Рис.57. Функция принадлежности нечёткого множества А к элементам множества U

B = {(0,9/u₁); (0,2/u₂); (1/u₃);(0,5/u₅); (0,8/u₆); (1/u₇)}

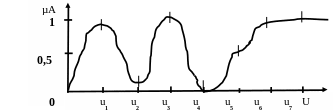
Рис.58. Функция принадлежности нечёткого множества В к элементам множества U

Операции:

1. . Объединение: (А В) µ_А(у) µ_В(у)/у, где max из двух µ; µ_А(у) µ_В(у) = max

U

(µ_А(у), µ_В(у)), тогда А В = {(0,9/u₁); (0,4/u₂); (1/u₃); (0,8/u₄); (0,5/u₅); (1/u₆); (1/u₇) }

2. Пересечение: А ∩В  µ_А(у) µ_В(у)/у , где µ_А(у) µ_В(у) = min (µ_А(у), µ_В(у)).

U

А ∩В = {(0,6/u₁); (0,2/u₂); (0,3/u₃); (0,5/u₅); (0,8/u₆); (0,6/u₇)}.

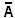
3. Дополнение (отрицание):  (1 - µ_А(у))/у; 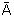={(0,4/u₁); (0,6/u₂); (0,7/u₃); (0,2/u₄); (0,5/u₅); (0,4/u₇)}; U

4. Сумма: А + В (А В) – (А ∩В); А + В = {(0,3/u₁); (0,2/u₂); (0,7/u₃); (0,8/u₄); (0,2/u₆); (0,4/u₇)}

5. Разность: А – В А ∩ ; А – В = {(0,1/u₁); (0,4/u₂); (0,5/u₅); (0,2/u₆)}

6. Произведение: А*В µ_А(у)*µ_В(у)/у; А*В = {(0,54/u₁); (0,8/u₂); (0,3/u₃); (0,25/u₅); (0,8/u₆); (0,6/u₇)} U

7. Возведение в степень: A^α µ^α_А(у)/у, α > 0.

U

8.Концентрирование: CON(A) A² Уменьшает степень принадлежности элемента нечеткого множества.

9. Растяжение: DIL (A) A ^0,5 Увеличивает степень принадлежности элемента нечеткого множества.

Пример:

Введем множество U = {1, 2, 3, 4, 5}

«Слабый студент» 1/1 + 0,8/2 + 0,6/3 + 0,3/4 + 0,2/5;

«Хороший студент» 0/1 + 0,4/2 + 0,6/3 + 1/4 + 0,8/5;

«Отличный студент» 0/1 + 0/2 + 0,4/3 + 0,5/4 + 1/5;

С помощью операций над нечёткими множествами можно создать новые нечёкие множества.

«Очень слабый студент» 1/1 + 0,64/2 + 0,36/3 + 0,09/4 + 0,04/5; (применяется операция концентрирования).

«Не слабый студент» 0,2/2 + 0,4/3 + 0,7/4 + 0,8/5;

«Очень не слабый студент» 0,04/2 + 0,16/3 + 0,49/4 + 0,64/5;

«Не очень слабый студент» 0,36/2 + 0,64/3 + 0,91/4 + 0,96/5;

Достоинства:

• Можно оперировать с нечеткими множествами;

• Можно определить количество нечеткости.

Недостатки:

• Субъективность коэффициентов µ.

Лекция 15

0. 7.1.3. Нечёткие отношения.

Наряду с нечеткими множествами и переменными в логике нечётких множеств вводится в рассмотрение нечеткое отношение R: ХУ как нечеткое подмножество декартова произведения множеств Х  У, которое определяется с помощью функции принадлежности двух переменных по формуле:

R  µ _R (х, у)/(х, у).

_{Х  У}

В общем случае n-арное отношение (n-отношение) определяется следующим образом. Пусть R — результирующее множество декартова произведения n множеств и µ - его функция принадлежности. Нечеткое n -отношение определяется как нечеткое подмножество R, принимающее какое-либо значение из µ в соответствии с формулой:

R =  µ _R (х₁,……………., х_n)/ (х₁,……………., х_n),

Х₁ …….. Х_n

х_i  Х_i, i = 1,……..,n

Пример. Допустим, что

Х= (Игорь, Ольга); У= (Владимир, Людмила)

Дружба = 0,6 (Игорь, Владимир) + 0,9 (Игорь, Людмила) + 0,8 (Ольга, Владимир) + 0,2 (Ольга, Людмила).

Отношения удобно задавать с помощью матрицы отношений µ ={ µ_ij }:

Владимир Людмила

Игорь 0,6 0,9

µ = Ольга 0,8 0,2

Для задания отношений между нечёткими множествами необходимо ввести понятие декартового произведения между нечёткими множествами.

Декартово произведение двух нечётких множеств А и В, определённых как подмножества областей рассуждения U и V соответ-ственно, определяется соотношением.

А  В =  µ_А(u) µ_В(v)/(u/v), где

UV

µ_А(u) µ_В(v) = min (µ_А(u), µ_В(v)), UV - декартово произведение областей рассуждения, которое определяется как:

UV={ (u,v)/ u U, v  V}.

Нечёткое произведение А  В является нечётким отношением U к V, так как оно представляет собой нечёткое множество упорядоченных пар (u,v) со степенью принадлежности µ_АВ (u,v), равной min (µ_А(u), µ_В(v))

Пример:

U=(u₁, u₂) ;

V=(v₁,v₂,v₃) ;

А = {(0,6/u₁); (0,4/u₂)} ;

B = {(0,9/v₁); (0,2/v₂); (1/v₃)} ;

Тогда:

А  В = min(0,6;0,9)/( u_1, v₁) + min(0,6;0,2)/( u_1, v₂) + min(0,6;1)/( u_1, v₃) + min(0,4;0,9)/( u_2, v₁) + min(0,4;0,2)/( u_2, v₂) + min(0,4;1)/( u_2, v₃) = 0,6/( u_1, v₁) + 0,2/( u_1, v₂) + 0,6/( u_1, v₃) +0,4/( u_2, v₁) + 0,2/( u_2, v₂) + 0,4/( u_2, v₃). Это произведение можно записать с помощью матрицы в следующем виде:

v₁ v₂ v₃

u₁ 0,6 0,2 0,6

u₂ 0,4 0,2 0,4

Свойства нечетких отношений:

Пусть R нечёткое отношение, построенное между элементами одной и той же области рассуждения U, тогда отношение обладает свойством:

• рефлексивности:

если µ_R(u, u ) = 1, отношение R— рефлексивное, u U;

если µ_R(u, u ) < 1 и > 0,5, отношение R — слаборефлексивное, u U;

если µ_R(u, u ) = 0, отношение R — антирефлексивное, u U;

если µ_R(u, u ) > 0, и < 0,5, отношение R — слабоантирефлексивное,

uU;

• симметричности µ_R(u, v ) = µ_R(v, u ), v,u U;

• транзитивности µ_R(u, v )  min (µ_R(u, z ), µ_R(z, v )) v,u,z U.

Любое отношение между нечёткими множествами строится как приведённое выше декартово произведение, а вид отношения определяется способом вычисления степени принадлежности µ_АВ (u,v), причём, для одного и того же отношения разные авторы предлагают различные способы вычисления µ_АВ (u,v).

Например, если в системе искусственного интеллекта с нечётким выводом допускается организация правил с одним выходом «ЕСЛИ А, ТО В», где А антецедент и В консеквент, а также правил с двумя выходами «ЕСЛИ А, ТО В, ИНАЧЕ С». При этом антецедент может быть сложным логическим выражением, включающим операции отрицания, дизъюнкции и конъюнкции. Для вычисления нечеткого отношения R, соответствующего этим правилам на нечетких множествах

А= µ_А(u)/u; В= µ_В(v)/v; и С=  µ_С(v)/v

U V V

используются следующие способы:

1) импликация Мамдани для правил с одним выходом:

R =  min {µ_А(u), µ_В(v)} /(u, v );

UV

2) максиминное правило с одним выходом:

R =  max{min [µ_А(u), µ_В(v)], [1- µ_А(u)]}/(u, v );

UV

3) максиминное правило с двумя выходами:

R =  max{min [µ_А(u), µ_В(v)], min ([1- µ_А(u)], µ_С(v)) }/(u, v );

UV

4) бинарное правило с одним выходом:

R =  min {max [(1-µ_А(u)), µ_В(v)], µ_А(u)}/(u, v );

UV

5) бинарное правило с двумя выходами:

R =  min {max [(1-µ_А(u)), µ_В(v)], max[µ_А(u),µ_С(v)]}/(u, v );

UV

6) импликация Лукасевича для правил с одним выходом:

R =  min {1, [1-µ_А(u) + µ_В(v)]} /(u, v );

UV

7) импликация Лукасевича для правил с двумя выходами:

R =  min { min [1,(1-µ_А(u) + µ_В(v))], [µ_А(u) + µ_С(v)]}/(u, v );

UV

8) импликация Геделя для правил с одним выходом:

R =  [µ_А(u) µ_В(v)], µ_А(u)}/(u, v );

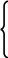UV g

1, если µ_А(u) µ_В(v) ;

где: µ_А(u) µ_В(v) =

g 0, если µ_А(u) >µ_В(v) ;

9) импликация Геделя для правил с двумя выходами:

R =  min {(µ_А(u) µ_В(v)),(1- [µ_А(u)  µ_С(v)])}/(u, v );

UV g g

Выбор способа реализации зависит от задачи и наглядности интерпретации результатов и обычно остаётся за пользователем системы.

Композиция нечетких отношений. Если знания представлены с помощью нечетких множеств и нечетких отношений, то для реализации логических выводов в нечеткой среде необходимо иметь возможность применения совокупности правил. Поскольку знания в виде правил формализуются нечеткими отношениями, нужно уметь осуществлять их композицию, которая может выполняться с помощью операции максиминной свертки.

Пусть R — нечеткое отношение из области U в область V, а S— нечеткое отношение из области V в область W тогда нечеткое отношение из области U в область W определим как свертку следующего вида:

R  S = max (min {µ_R(u,v), µ_S(v,w)})/(u, v);

v U W

Поясним применение максиминной свертки на примере.

Пусть R — нечеткое отношение между множествами U и V, которые представляют собой совокупности натуральных чисел от 1 до 4. Смысл отношения R соответствует правилу:

«ЕСЛИ u — малые числа, ТО v — большие».

U= V= {1,2,3,4};

F= 1/1+0,6/2+0,1/3-нечёткое множество малых чисел;

G=0,1/2+0,6/3+1/4- нечёткое множество больших чисел.

Определим отношение S из Vв W с этой целью на V определим понятие «немалые числа», которое будет дополнением введенного ранее нечеткого множества и обозначим его F1= 0/1+0,4/2+0,9/3+1/4 УI. Введем множество W= {1,2,3,4} и определим на нем понятие «очень большие числа», которое обозначим H. К этому понятию числа 1 и 2 имеют степень принадлежности, равную 0, число З имеет значение принадлежности 0.5, и только 4 принадлежит со степенью, равной 1:

H = 0.5/З + 1/4. Отношение S между полными множествами V и W сформулируем в виде правила:

«ЕСЛИ v — немалые числа, ТО w — очень большие числа».

Построим нечеткие отношения R и, используя первое правило (импликация Мамдани):

R =  min {µ_U(u), µ_V(v)} /(u, v );

UV

µ_R(u_i, v_j ) = min (µ_U(u_i ), µ_V(v_j )) v, u U. i, j=1,2,3,4

µ_U= {1; 0,6; 0,1; 0}

µ_V= {0; 0,1; 0,6; 1}

0 0,1 0,6 1

R= 0 0,1 0,6 0,6

0 0,1 0,1 0,1

0 0 0 0

µ_S(v_i, w_j ) = min (µ_V(v_i ), µ_W( w_j )) v, w V,W. i, j=1,2,3,4

µ_V = {0; 0,4; 0,9; 1}

µ_W= {0; 0; 0,5; 1}

0 0 0 0

S= 0 0 0,4 0,4

0 0 0,5 0,9

0 0 0,5 1

Вычислим максиминную свертку нечетких отношений R  S результат которой должен соответствовать последовательному приме-нению двух правил: «ЕСЛИ u — малые числа, ТО v — большие» и «ЕСЛИ v — немалые числа, ТО w — очень большие числа».

0 0,1 0,6 1 0 0 0 0 0 0 0,5 1

R  S = 0 0,1 0,6 0,6  0 0 0,4 0,4 = 0 0 0,5 0,6

0 0,1 0,1 0,1 0 0 0,5 0,9 0 0 0,1 0,1

0 0 0 0 0 0 0,5 1 0 0 0 0

µ_{R  S} (v_i, w_j ) = max {min [µ_R(u_i, v_j ), µ_S(v_i, w_j )], min [µ_R(u_i, v_j+1 ), µ_S(v_i+1, w_j )], min [µ_R(u_i, v_j+2 ), µ_S(v_i+2, w_j )], min [µ_R(u_i, v_j+3 ), µ_S(v_i+3, w_j )]}

При парных сравнениях элементов i-й строки и j-го столбца из них выбирается наименьший, затем из четырех минимальных элементов выбирается максимум, который является результатом, и записывается в ячейку с координатами I,j. Результирующее нечеткое отношение показывает взаимосвязь областей U и W.