4.1.2. Задачи, решаемые с помощью графов.

1. Задача поиска наикратчайшего пути на графе.

Задан ориентированный граф.

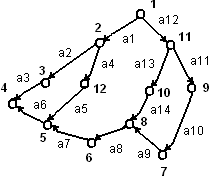
Рис.28. Ориентированный граф

Решение любой задачи оптимизации: f (x₁,….,x_n) → min / max

M (1,5) ∑ α _i = min (i = 1,…,n)

Задача решается методом «ветвей и границ».

2. Транспортная задача.

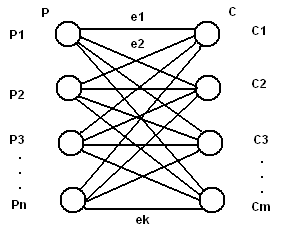
Рис.29. Транспортная сеть

Р – производители некоторой продукции;

С – потребители продукции;

е₁, е₂,…,е_к – маршруты;

к = m*n

Есть некий заказ Р, который состоит из подзаказов р₁, р₂, …, р₃ и объема продукции, которую необходимо потребить.

Р = ∑р_i (i = 1,…,n )

C = ∑c_j (j = 1,…,m)

P = C

Ограничения: Каждый маршрут имеет свой вес, свои затраты Se₁,…,Se_k и ограничения на пропускную способность. Se₁d₁,…,Se_kd_k

Необходимо найти маршруты от производителей к потребителям, чтобы

∑Se_l → min (e = 1,…,k)

Алгоритм Форда-Фолкерсона.

3. Задача о назначении (задача коммивояжера).

Есть несколько городов и дороги между ними. Найти маршрут коммивояжера, чтобы он посетил каждый город только 1 раз.

Рис.30. Сеть коммивояжёра

Это задача целочисленного программирования (оптимизации). Особенность: задачи легко ставятся, но тяжело решаются.

4. Задача о назначении работ.

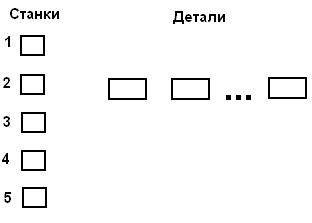
Рис.31. Станки и детали

D1 (t₁`, t<sub>2</sub>`, t₃`, t<sub>4</sub>`, t₅`)

D2 (t₁``, t<sub>2</sub>``, t₃``, t<sub>4</sub>``, t₅``)

Есть n станков и n деталей. Каждая деталь должна обрабатываться на 5-ти станках, причем время обработки разное для каждой детали.

t₁`, t<sub>2</sub>`, t₃`, t<sub>4</sub>`, t₅` – время обработки детали 1 на 1-ом,…,5-ом станке.

t₁``, t<sub>2</sub>``, t₃``, t<sub>4</sub>``, t₅``- время обработки детали 2 на 1-ом,…,5-ом станке.

В какой последовательности запустить детали на обработку, чтобы время выполнения заказов было минимальным.

Лекция 10

4.2. Представления знаний в виде семантических сетей.

Основные понятия:

Описание сетевых моделей (общий случай): Н = < I, C₁, C₂, …, Cn, Г >

I – множество информационных единиц.

C₁, C₂, …, Cn – множество типа связи между информационными единицами.

Г – отображение, которое задает связи из C₁ … Cn между информационными единицами, входящими в I.

По сути является графом.

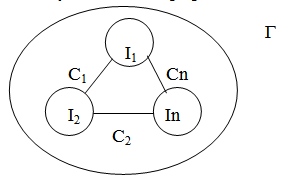
Рис.32. Сетевая модель- Н семантической сети

В зависимости от типа связи различают:

1. функциональные сети

2. семантические сети (наиболее распространены)

3. сценарии

   • В функциональных сетях: дуги отражают свойства вершин, из которых они выходят (вершины – понятия). С использованием вершин (понятий), в которые они входят

   • Семантические сети: способ представления знания, объединяющий в себе свойства функциональных сетей и сценариев

   • Сценарии: используют однородные сети, в которых в качестве единственного отношения используются отношения нестрогого порядка.

Сценарии (описание порядка действий).

Сценарий представляется некоторой сетью, где вершины – понятия, а дуги – связи описывающие отношения специального типа. Эти отношения обладают свойством: если между вершинами x и y существует множество путей р₁, р₂, …, р_n наличествуют оба фактора А и В, отвечающие вершинам х и у, то имеет место по крайней мере совокупность этих факторов, соответствующим вершинам на одном из путей, соединяющих х и у.

К таким отношениям относятся:

• отношение следствия

• причинное отношение

• отношение часть-целое

Пример. Сетевая модель задачи «Электропылесос. Разбор пылесоса»

Рис.33. Семантическая сеть разбора пылесоса

1 – пылесос

2 – верхняя часть

3 – уплотнительное кольцо с фильтром

4 – нижняя часть

5 – электродвигатель с вентилятором

6 – выключатель

7 – рассеиватель

8 – шнур

С тавим задачу - достать электродвигатель: Взять пылесос снять верхнюю часть

достать двигатель.

Сценарии используются для формирования допустимых планов по достижению цели. Также они применяются для выполнения описания новых фактов в интеллектуальной системе. Например, если известен факт, что в комнате работал пылесос, то значит, работал вентилятор, шнур, выключатель и др. Или, что шнур пылесоса находился в момент времени t, в комнате, когда там работал пылесос.

Сценарий позволяет описывать предметы, их свойства в пространстве и во времени.

Семантические сети

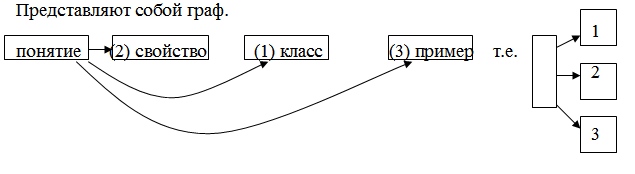
Рис.34. Стандартная схема определения любого понятия

Новое понятие вводится через свойства, его класс, примеры. Следовательно, получается ясный образ. Разнообразные психологические исследования, работы по информатике определили, что основой для определения того или иного понятия является множество отношений или взаимосвязей с другими понятиями.

Среди этих связей выделим основные:

• класс, которому принадлежит данное понятие

• свойство, выделяющее понятие из всех прочих понятий этого класса

• пример, данного понятия

шумное

^{свойство}

свойство посетители

заведение класс место

класс закусочная

класс

три пескаря харчевня

пример

Рис.35. Пример определения понятия

Мы можем определить любые понятия через класс, пример и свойства.

Для обобщенного представления понятий структуры вводится следующий формализм:

• дуга класс – HAS – A (класс – подкласс)

• дуга свойство – название свойства

• дуга пример – IS – A (элемент класса)

Пример с использованием дуг про харчевню.

место

HAS-A HAS-A имеет

харчевня заведение посетители

IS-A HAS-A

«три пескаря» закусочная

есть

шумное

Рис.36. Пример описания предметной области

Пример: Путь, что имеет харчевня? заведение посетители.

Следовательно: харчевня имеет посетителей.

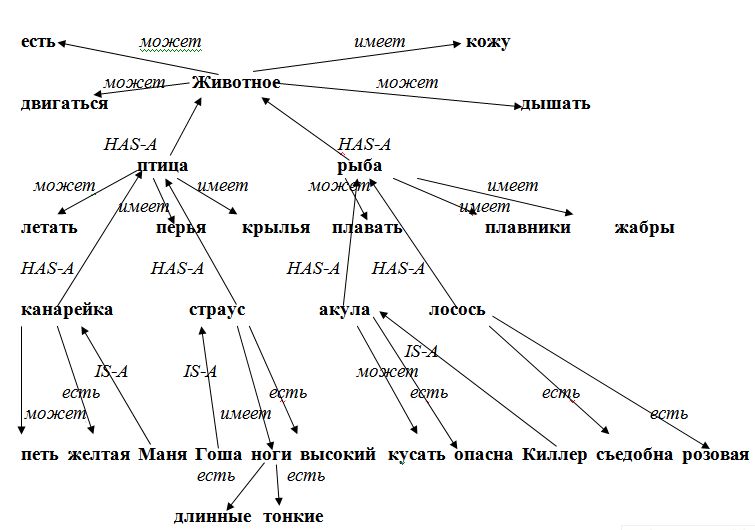
Схема 2. Классификация

Пример. «Может ли акула летать?» Нет, потому что нет пути при данной ориентации графа.

«Что может Маня?» Летать, есть и т.д.