3.3. Вывод в системах искусственного интеллекта с логическим представлением знаний.

3.3.1. Правило резолюции.

В 1930 году Эрбран в своей докторской диссертации по математике предложил оригинальный метод доказательства теорем в формальных системах первого порядка. Этот метод основан на теореме «О Резолюции».

Теорема О Резолюции: Пусть имеется формула F₁ в стандартной форме представления

F₁ = C₁ ^ C₂ ^ …^ (P L_i) ^…^ (P Lj) ^…^ C_m

(P L_i) - Дизъюнкта Хорна

Из F₁ может быть получена формула F₂= C₁ ^ C₂ ^ …^ ^…^ C_m ^ (L_i L_j ), образующаяся из формулы F₁ путем присоединения к ней резольвенты, оставшейся в ней от 2-х родительских предложений.

Теорема гласит: Если формула F₂ противоречива, то F₁ так же противоречива.

Предложения Сi = (P L_i) и Сj =(P Lj) являются родительскими по отношению к предложению С = L_i L_j (резольвенты).

Сi ^ Сj = (P L_i) ^ (P Lj) = (P P) ^ (L_i  Lj) = (L_i L_j ), Так как

Предположения:

F₁ = C₁ ^ C₂ ^ …^ (P L_i) ^ (P Lj) ^…^ C_m = F₂= C₁ ^ C₂ ^ …^ …^ C_m ^ (L_i L_j )

И если (L_i L_j ) = 0- пустая резольвента, то F₂=0 и следовательно F₁= 0.

Резольвента – результат выполнения операции конъюнкции двух родительских предложений, имеющих вид дизъюнкта Хорна. В одной операции стоит логическое предложение, а в другой - обязательно его отрицание.

Пустая резольвента – дизъюнкция, слагаемые которой являются 0.

Доказательство противоречивости F₂ сводится к методической резолюции, заключающейся в поиске пустой резольвенты. Если это происходит, то и F₁ тоже противоречиво.

Робинсон пришёл к заключению, что правила вывода, которые следует применять при автоматизации процесса доказательства, не обязательно должны совпадать с правилами вывода, используемыми человеком. Он обнаружил, что общепринятые правила вывода, например, правило modus ponens (раздел 2.2.2. таблица 1 правило 1), специально сделаны “слабыми”, чтобы человек мог интуитивно проследить за каждым шагом процедуры доказательства. Робинсон открыл более сильное правило вывода, которое он назвал резолюцией (или правилом резолюции).

Это правило трудно поддаётся восприятию человека, но эффективно реализуется на компьютере. Правило резолюции сходно с правилом modus tollendo ponens (раздел 2.2.2.,таблица 1, правило 4). Правило резолюции действует следующим образом. Две дизъюнкты Хорна могут быть резольвированы (сопоставимы) друг с другом, если одна из них содержит позитивную элементарную формулу а другая - соответствующую негативную элементарную формулу с одним и тем же обозначением предиката и одинаковым количеством аргументов, и если аргументы обоих элементарных формул могут быть унифицированы (согласованы) друг с другом. Такие два дизъюнкта называются родительскими дизъюнктами. Если в качестве аргумента предиката элементарной формулы выступает переменная, то она унифицируема с любой константой.

Если в резольвируемых дизъюнктах Хорна переменная встречается более одного раза и эта переменная в процессе резолюции унифицируется с константой, то резольвента будет содержать данную константу на тех местах, где рассматриваемая переменная располагалась в элементарных формулах исходных дизъюнкт. В результате этого получится новая дизъюнкта Хорна, называемая резольвентой и являющаяся новой аксиомой теории. Если при резолюции двух дизъюнкт, входящих в состав теории, получается пустой дизъюнкт, то эта теория противоречива.

Примеры:

1. Рассмотрим теорию, состоящую из двух дизъюнкт:

ab,c 

b,cb,c 

Поскольку в дизъюнкте содержится негативная элементарная формулаb, c, в дизъюнкте - соответствующая позитивная элементарная формула b, c и аргументы обоих предикатов могут быть унифицированы, то дизъюнкт  может быть резольвирован с дизъюнктом . Дизъюнкты  и  являются родительскими дизъюнктами. В результате этого получается дизъюнкт  - резольвента, который становится новой аксиомой теории:

ab,c 

После выполнения данной резолюции при последующих резолюциях можно воспользоваться любой из дизъюнкт ,  и .

2. Рассмотрим теорию, состоящую из двух дизъюнкт:

ab,c 

с,cb,c 

Дизъюнкты  и  не резольвируются друг с другом, т.к. аргументы предиката  не поддаются унификации.

3. Рассмотрим теорию, состоящую из двух дизъюнкт:

ac,b 

x,yx,y 

Для того, чтобы эти дизъюнкты резольвировали необходимо унифицировать переменные т.е. во всех предикатах “x” заменить на “c”, а “y” заменить на “b”. В результате этого получается новый дизъюнкт , в котором переменные, служившие аргументами в предикате , теперь заменены на константы.

ac,b 

4. Рассмотрим две элементарные формулы, которые после многократных резолюций вошли в теорию и приняли следующий вид:

b,c 

b,c 

Так как теория представляет из себя систему аксиом, связанных знаком “конъюнкция”, то  и  представляет из себя следующее выражение: b,cb,c, которое всегда ложно и следовательно эта теория противоречива. Если дизъюнкты  и  резольвируются друг с другом, то получающаяся

резольвента называется пустым дизъюнктом. Таким образом вывод пустой дизъюнкты свидетельствует о пртиворечивости данной теории.

Алгоритм, позволяющий автоматизировать процесс доказательства теорем на основе правила резолюции, состоит из следующих шагов:

1. Добавление к системе аксиом дизъюнкта, являющегося отрицанием доказуемой теоремы.

2. Поиск среди дизъюнкт (аксиом) теории для добавленной дизъюнкты резольвируемой с ней второй родительской дизъюнкты.

3.Унификация переменных.

4.Выполнение правила резолюции и формирование резольвенты.

5.Если резольвента пустая, то теорема доказана и окончание работы алгоритма, если нет - присоединение резольвенты в виде новой дизъюнкты к существующей системе дизъюнкт (аксиом) теории и переход к шагу 2.

Пример: Пусть имеется некоторая теория, состоящая из следующих аксиом (дизъюнкт):

aa,b 

x,yx,y 

b 

a,b 

Необходимо доказать, что утверждение a  является следствием данной теории.

Доказательство проведём в соответствии с предложенным алгоритмом.

Шаг 1. Добавим отрицание доказуемого утверждения к системе аксиом теории и получим новую систему аксиом:

aa,b 

x,yx,y 

b 

a,b 

a 

Шаг 2. Дизъюнкты  и  являются родительскими.

Шаг 3. У родительских дизъюнкт аргументы унифицированы.

Шаг 4. Выполняя правило резолюции, получаем следующую резольвенту:a,b .

Шаг 5. Резольвента не пустая, следовательно, присоединяем её к существующей системе аксиом, получаем новый набор аксиом и переходим к шагу 2.

aa,b 

x,yx,y 

b 

a,b 

a 

a,b 

Шаг 2. Две резольвенты  и  являются родительскими.

Шаг 3. Проводя унификацию переменных в родительских дизъюнктах, получим следующую систему аксиом:

aa,b 

a,ba,b  

b 

a,b 

a 

a,b 

Шаг 4. Выполняя правило резолюции, получим следующую резольвенту:a,b 

Шаг 5. Резольвента не пустая, следовательно присоединяем её к существующей системе аксиом, получаем новый набор аксиом и переходим к шагу 2.

aa,b 

x,yx,y 

b 

a,b 

a 

a,b 

a,b 

Шаг 2. Две резольвенты  и  являются родительскими.

Шаг 3. У родительских дизъюнкт аргументы унифицированы.

Шаг 4. Выполняя правило резолюции, получаем пустую резольвенту.

Шаг 5. Резольвента пустая, следовательно утверждение доказано и алгоритм заканчивает свою работу.

Отличия в различных алгоритмах, реализующих правило резолюции заключаются в основном в различии стратегии поиска родительских дизъюнкт.

ПРИМЕР:

F₁ = C₁ ^ C₂ ^ C₃ ^ C₄

Проблема: Каким образом строить поиск пустой резольвенты.

А) C₁ и C₄ C₅ =

Б) C₂ и C₃ C₆ = Р

В) C₅ и C₆ C₇ = (  0)  (Р 0) = (0  0) пустая резольвента.

Значит F₁ противоречиво.

Если F₁ истина, то остановкой для алгоритма является отсутствие пар родительских предложений.

В случае использования предикатов, когда аргументом может быть переменная и константа, необходимо найти такие значения переменной, при которых данная формула F₁ будет противоречива. Такая подстановка (константы вместо переменных) называется унификацией.

ПРИМЕР:

x, y, z, t, v – переменные.

a, b, c – константы.

А) F₁ и F₄ S₁ = {x / a, y / z};

Б) F₂ и F₄ S₂= {t / b};

B) F₂ и F₄ S₃= {t / c};

Г) F₂ и F₅ S₄= {t / b};

Д) F₂ и F₈ S₅= {t / с};

F₉ = пусто

Проблема: Чтобы использовать «Пролог» и доказательства, необходимо сформулировать исходные аксиомы и выходное целевое выражение в виде произведения дизъюнкт Хорна.

ПРИМЕР: Пусть высказаны следующие утверждения:

1. Кто может читать, тот грамотный.

2. Дельфины не грамотны.

3. Некоторые дельфины обладают интеллектом.

4. Некоторые из тех, кто обладает интеллектом не могут читать.

Необходимо доказать.

Общее выражение имеет вид:

исправить И(Х) без отрицания.

После преобразований (исключения кванторов, введения сколемовской переменной, исключения связок импликации, введения новых переменных) получаем следующую систему предложений:

1. 

2. 

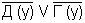
3. а) Д (А)

б) И (А)

А – сколемовская переменная.

Отрицание утверждения, которое нужно доказать, имеет вид:

4.*

Одно из возможных доказательств создает следующую последовательность резольвент:

5. Ч(А) резольвента из 3 б) и 4*, и замена Z на A.

6. Г(А) резольвента из 5 и 1, и замена Х на A.

7. резольвента из 6 и 2, и замена У на A.

8. Пустая резольвента из 7 и 3 а).

Данный вывод можно представить в виде графа вывода. Вершины графа помечены предложениями. Когда два предложения C_i и C_j создают резольвенту r_ij, то мы образуем новую вершину, помеченную r_ij, причем ребра связаны с вершинами C_i и C_j.

C_i и C_j - Родители для r_ij

r_ij - является потомком C_i и C_j

Опровержение на основе резолюций может быть представлено деревом опровержения, корневая вершина которого помечена предложением NIL.

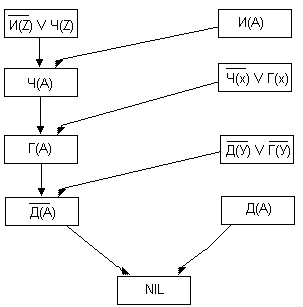
Рис.12. Стратегии поиска родительских предложений