Лекция 6

Глава3 Представление и вывод знаний в системах искусственного интеллекта на основе логических моделей.

3.1. Основы математической логики

Термин логика происходит от греческого слова logos, что значит мысль, слово, разум, закономерность, и используется как для обозначения совокупности правил, которым подчиняется процесс мышления, отражающий действительность, так и для обозначения науки о правилах рассуждения и тех формах, в которых она осуществляется.

3.1.1. Классификация и определение логик, алгебр, исчислений, теорий.

За время своего развития в математике было введено громадное количество различных понятий и определений, отражающих представления их авторов о наиболее истинном математическом описании реальной действительности или о единственно верном решении возникающих математических проблем. К наиболее фундаментальным определениям следует отнести понятия: логика, алгебра, исчисление, и теория. Анализ содержания этих понятий, установление их взаимосвязей, определение исторической последовательности введения этих понятий позволяет увидеть конечные цели введения той или иной математической абстракции. Здесь предлагается одна из возможных схем классификации этих понятий. (Схема 1)

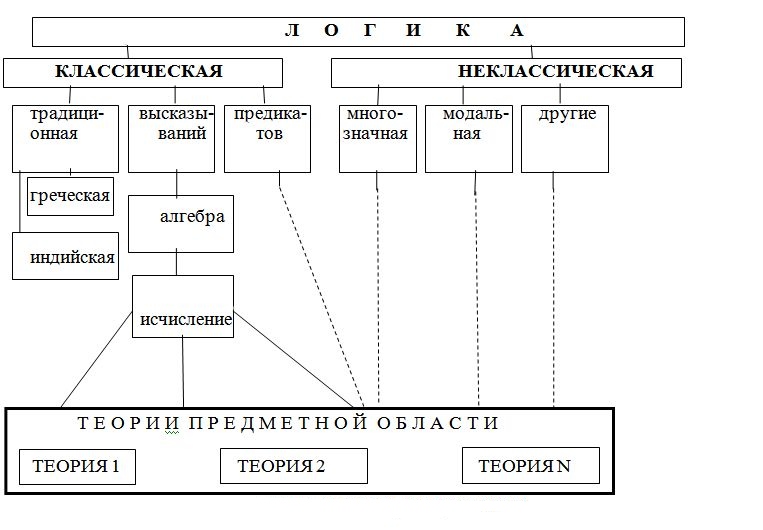
Схема 1. Классификация логики

Первоначально логика зародилась и развивалась в недрах философии единой нерасчленённой науки, которая объединяла всю совокупность знаний об объективном мире и о самом человеке и его мышлении. В традиционной логике законы и формы правильного мышления изучались в рамках ораторского искусства- одного из средств воздействия на умы людей, убеждения их в целесообразности того или иного поведения. Так было в Древней Греции, Древней Индии, Древнем Китае, Древнем Риме, средневековой России. Но в искусстве красноречия логический момент выступает ещё как подчинённый, поскольку логические приёмы служат не столько цели достижения истины, сколько цели убеждения аудитории.

Развитие науки логики на протяжении ряда столетий протекало по двум направлениям. Одно из них начиналось с древнегреческой логики (в особенности с логики Аристотеля), на основе которой развивалась логика в Древнем Риме, затем в Византии, Грузии, Армении, арабоязычных странах Ближнего Востока, в Западной Европе и России. Другое направление имело своим истоком индийскую логику, на основе которой развивалась логика в Китае, Тибете, Монголии, Корее, Японии, Индонезии, на Цейлоне.

Содержание традиционной логики соответствует первому этапу развития формальной логики. Необходимо отметить, что переходной фазой ко второму этапу является введение в традиционной логике понятия высказывание и разработка правил вывода применимых к высказываниям.

Второй этап - это появление математической (или символической) логики. Немецкий философ Г.В. Лейбниц (1646-1716) по праву считается основоположником этого этапа. Начиная с Лейбница, в логике используется в качестве метода исследования метод формализации, который традиционная логика относила только к методам математического исследования, а Лейбниц показал, что он имеет общенаучный характер. Лейбниц пытался построить универсальный язык, с помощью которого споры между людьми можно было разрешать посредством вычислений. В XIX в. математическая логика получила интенсивное развитие в работах Д. Буля (разработка алгебры высказываний), Э. Шрёдера (введение понятия логического исчисления), Г. Фреге (создание логики предикатов). Со времени своего возникновения и до двадцатых годов XX в. логика преимущественно развивалась в направлении формализации каталогизирования правильных способов рассуждений в пределах двух значений истинности. Суждения могли быть либо истинными, либо ложными. Такая логика именовалась классической или двузначной.

Третий этап развития математической логики связан с созданием неклассических логик, которые оперируют либо бесконечным множеством значений истинности, либо конструктивными (по сравнению с классической логикой) методами доказательства истинности суждений, либо модальными суждениями, либо исключают отрицания, имеющиеся в классической логике. В многозначных логиках число значений истинности аргументов и функций может быть любым конечным и даже бесконечным числом. К наиболее известным в этой области можно отнести работы Я. Лукасевича (введение трёхзначной системы), Гейтинга (введение трёхзначной системы с новыми операциями отрицания и импликации), Д.А.Бочвара (введение трёхзначной логики с целью разрешения парадоксов классической математической логики методом формального доказательства бессмысленности определённых высказываний), Г. Рейхенбаха (введение трёхзначной логики для описания явлений квантовой механики), Поста (введение n - значной логики). Развитие многозначных логик подтверждает мысль, что истина всегда конкретна, а также положение об относительном характере конкретно-научных знаний: то, что является тождественно-истинным в одной логической системе, не оказывается тождественно-истинным в другой. В классической двузначной логике рассматривались простые и сложные ассерторические суждения, т.е. такие, в которых не установлен характер связи между субъектом и предикатом.

Например: “Морская вода - солёная” или “Дождь то начинал хлестать тёплыми крупными каплями, то переставал”. В модальных суждениях раскрывается характер связи между субъектом и предикатом или между отдельными простыми суждениями в сложном модальном суждении. Например: “Необходимо соблюдать правила уличного движения” или “Если будет дуть попутный ветер, то, возможно, мы приплывём в гавань до наступления темноты”. Модальными являются суждения, которые включают модальные операторы (модальные понятия), т.е. слова “необходимо”, “хорошо”, “возможно”, “невозможно”, “случайно”, “запрещено” и многие другие. Модальные суждения рас-сматриваются в специальном направлении неклассической логики - в мо-дальной логике. Возникновение модальной логики как системы связано с именем американского логика и философа К.И. Льюиса. В этом направлении известны работы Ф.В. Аккермана и Р. Фейса. Интересна интерпретация модальных логик. Известный австрийский философ и логик Р. Карнап пытался интерпретировать модальные понятия с помощью, так называемой теории “возможных миров”, в которой допускается наличие множества “миров”, один из которых - действительный, реальный мир, а остальные - возможные миры. Необходимым объявляется то, что существует во всех мирах, возможным - то, что существует хотя бы в одном. К другим логикам можно отнести: интуиционистскую (Л. Брауэр, Гейтинг), конструктивную (А.Н. Колмогоров, В.И. Гливенко, А.А. Марков), паранепротиворечивую (С. Яськовский, Ньютон да Коста). Вообще, к настоящему времени, известно более семидесяти логик, соответствующих различным философским идеям и лежащих в основе решения множества научно-технических задач.

Для каждой из логик может быть построена своя алгебра. Содержанием этой алгебры являются операции над элементами данной логики: высказываниями, предикатами, модальными операторами и т.д. Эти алгебры могут отличаться друг от друга набором и определением операций над элементами логики. Также для каждой логики может быть создано своё исчисление, которое строится по схеме: алфавит, правила образования формул, правила преобразования (вывода). Формулы образуются из элементов логики с использованием операций соответствующей алгебры, правила преобразования (вывода) позволяют определить истинность конкретной формулы в данном исчислении. В более широком смысле любое исчисление является математической моделью процесса перехода от посылок к следствию, проводимого по определённым правилам вывода.

Для того чтобы использовать методы той или иной логики применительно к конкретной области знаний (предметной области) необходимо построить соответствующую теорию, состоящую из набора аксиом. Если теория адекватно описывает заданную предметную область, то все факты из этой области являющиеся истинными, будут следствиями аксиом этой теории, а ни один факт, являющийся ложным, не будет следствием данных аксиом. Адекватно построенная теория позволяет проверять те или иные гипотезы из данной предметной области формальным образом, что является математической основой решения конкретных практических в этой области знаний. Подробнее о методах построения теории в предметной области, т.е. онтологии и её практи-ческом использовании в лекции 11.