2.6. Понятие модели.

Центральным местом предлагаемой методики - является процесс построения адекватной модели. Любые выводы сделанные на основе тех или иных моделей верны с точностью адекватности модели целям и предметной области. Прежде чем перейти к методам доказательства адекватности моделей, рассмотрим само понятие модели.

Модель - это естественный или искусственный объект, находящийся в соответствии с какой-либо из сторон изучаемого или создаваемого объекта.

Моделирование - означает осуществление каким-либо способом отображения или воспроизведения действительности для изучения имеющихся в ней закономерностей.

Можно дать более обобщённое понятие модели и моделирования.

Моделированием является любой метод практического или теоре-тического, мысленного или опытного оперирования объектом. При этом используется вспомогательный промежуточный искусственный или естественный “квазиобъект”, находящийся в каком-либо объективном соответствии с познаваемым или создаваемым объектом и называемый моделью. Рассмотрим одну из возможных классификаций моделей (рис. 13).

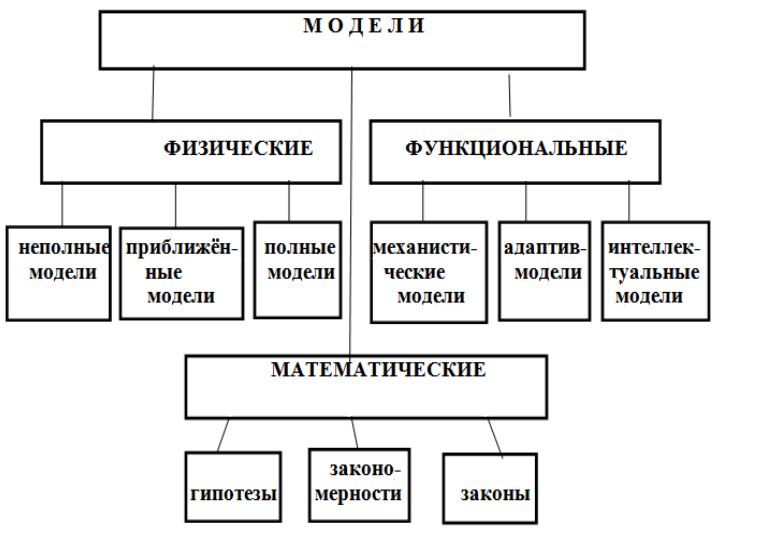
Рис.13.

Физические модели - сохраняют природу физических явлений, происходящих в объекте моделирования. Физические модели по степени адекватности реальным объектам можно разделить на три класса: неполные, приближённые и полные.

Полные модели - моделируют и пространственные и временные отношения, существующие в реальном объекте.

Например: Модель самолёта в аэродинамической трубе.

Неполные модели - моделируют либо пространственные, либо временные отношения, существующие в реальном объекте.

Например: Макетирование архитектурных ансамблей.

Приближённые модели - приближённо моделируют и пространственные, и временные отношения или либо пространственные, либо временные отношения, существующие в реальном объекте.

Например: Геометрические модели молекул - приближённо моделируют пространственные свойства молекул.

Адекватность физических моделей достигается за счёт подобия физических процессов, происходящих в модели и объекте, либо за счёт подобия математических выражений, описывающих физические процессы, происходящие в модели и объекте, и вычисления соответствующих масштабных коэффициентов на основе теории подобия.

Метод решения задач, использующий физические модели, заключается в проведении активных экспериментов с моделью объекта с дальнейшей обработкой результатов экспериментов с целью предсказания поведения реального объекта в штатных и критических ситуациях.

Математические модели - представляют собой формализованное описание пространственно-временных отношений объекта.

Гипотезы - связаны с построением на основе логики высказываний качественных феноменологических (объясняющих явления) моделей.

Например: Планетарная модель атомов.

Закономерность – представляют формальное количественное описание свойств объекта и его пространственно - временных отношений, подтверждённое некоторым числом измерений.

Например: Закономерность выпадения орла или решки.

Законы – представляют формальное количественное описание свойств объекта и его пространственно - временных отношений, позволяющее прогнозировать поведение объекта.

Например: Законы классической механики.

Адекватность математических моделей достигается путём многократных экспериментов с объектом, подтверждающих с точностью до ошибки измерения выявленную формальную связь между количественными значениями свойств предметов и свойств отношений предметов, участвующих в процессе.

Метод решения задач, основанный на математических моделях заключается в логическом или математическом выводе количественных значений свойств предметов или отношений, исходя из известных значений свойств.

Особое место в классификации занимают функциональные или кибернетические модели. Если физические и отчасти математические модели копируют предметы и отношения, составляющие объект, и тем самым, объясняя функционирование объекта, то функциональные модели копируют только поведение системы, не раскрывая внутреннего устройства объекта.

Например: Функциональная модель птицы - воздушный шар т.к. тот и другой объекты летают.

Механистическая модель – модель, в которой набор функций жёстко определён.

Например: заводная игрушка.

Адаптивная модель – изменяет набор функций в зависимости от внешних условий и воздействий, но изменения функций происходят по жёсткому алгоритму.

Например: механическая мышка в лабиринте, снабжённая фотоэлементом и программой поиска свободного направления.

Интеллектуальная модель - изменяет набор функций и программу поведения в зависимости от внешних условий и воздействий, т.е. обладает обучаемостью.

Например: нейронная сеть.

Непосредственно с видом модели связан метод доказательства адекватности модели. Также с видом модели связан и метод решения задач. Здесь будем рассматривать методы решения задач анализа т.к. для задач синтеза методом решения, как уже говорилось выше, является создание соответствующей технологии, описание которой выходит за рамки данного пособия.