2.2. Теория множеств - математический аппарат описания онтологии.

2.2.1. Основные понятия и определения.

Под множеством M понимается любое объединение в одно целое определенных вполне различаемых объектов, которые называются элементами множества M.

= -знак равенства. -пустое множество.  - принадлежит множеству.  - не принадлежит множеству . -включение в множество.

Чтобы задать множество, надо или перечислить все его элементы (для конечных множеств) или указать общее свойство всех его элементов.

X 1= X2 - множество X1 равно множеству X2.

M = - M - пустое множество.

a  A - a принадлежит множеству A.

a  A - a не принадлежит множеству A.

 B - A является подмножеством множества B.

A={a1,a2,..........,an} - множество образованное из n-элементов.

Лекция 4

2.2.2.Операции над множествами

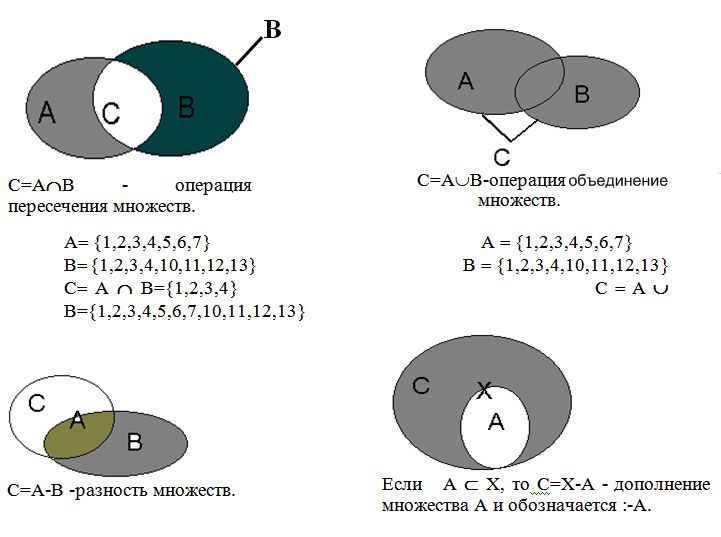
A 1,2,3,4,5,6,7 A 1,2,3,4

B 1,2,3,4,10,11,12,13 Х  1,2,3,4,10,11,12,13

C A – B=5,6,7 C Х – A = 10,11,12,13

Теоретико-множественный подход вследствие своей универсальности может быть использован для формального описания любых задач.

2.2.3. Декартово произведение множеств

Декартово (прямое) произведение М и N множеств– это множество М  N, состоящее из всех возможных вариантов упорядоченных пар, первый и второй компоненты которых принадлежат соответственно множествам M и N.

М × N = (x₁, y₁), (x₁, y₂), ….(x₁, y_k), (x₂, y₁)….(x_n, y_k)

M = { x_1, x_2, … x_n} где (x_i, y_j) – вектор

N = { y_1, y_2, … y_k} x_{i _}-_{_}первая координата вектора,

y_j - вторая координата вектора.

Обобщение на случай n-множеств.

Декартово (прямое) произведение М₁, М₂, … М_n – множеств – это множество М₁ × М₂× … ×М_n, состоящее из векторов, каждый из которых состоит из n координат, где первая координата принадлежит М₁ , вторая принадлежит М₂, …., n - координата принадлежит М_n.

Пример:

М = {1, 2, 3, 4}

N = {-5, -2, -1, 0, 2, 3}

М × N = {(1, -5),(1, -2),(1, -1),(1, 0),(1, 2),(1, 3),(2, -5),(2, -2),(2, -1),(2, 0),

(2, 2),(2, 3),(3, -5),(3, -2),(3, -1),(3, 0),(3, 2),(3, 3),(4, -5),(4, -2),(4, -1),(4, 0),

(4, 2),(4, 3)}

2.2.4. Отношения и их свойства.

Пусть М₁, М₂, … М_n - некоторые множества, отношением r порядка n или n–арным отношением между элементами множеств М₁, М₂, … М_n называется подмножество R декартового произведения этих множеств для элементов которого выполняется данное отношение.

R М₁ М₂ … М_n

Для определения элементов подмножества R необходимо для всех элементов множества М₁ М₂ … М_n провести процедуру проверки выполнения отношения r.

Отношения двух множеств называется бинарным, отношение трех множеств – тернарным, отношение n множеств – n-арным.

Для двух множеств определение примет следующий вид:

Если ρ – бинарное отношение между элементами множеств M = { x_1, x_2, … x_n} и N = { y_1, y_2, … y_k} и упорядоченная пара (x_i, y_j) принадлежит   М × N, то говорят, что элемент x_i находится в отношении ρ с элементом y_j. В противном случае элемент x_i, не находится в отношении ρ с элементом y_j.

Свойства отношений

Задано бинарное отношение R на множестве М. Это значит, что R М × М .

1. Рефлексивность – это равенство самому себе. a R a для всех a  M. Отношение «равенство» всегда рефлексивно. Отношение «больше» – не рефлексивно.

2. Транзитивность: Если a R b и b R c, то a R c. a, b, c  M. Отношение «родственник» - транзитивно.

3. Симметричность: Если a R b, то b R a для всех a, b  M. Отношение «родственник» - симметрично.

4. Антисимметричность: Если a R b и b R a, то a = b. Отношение «синонимы»: глаз = око антисимметрично.