54) Агрегатные индексы. Система индексов

Мы познакомились с построением сводных индексов на основе индивидуальных. Однаковозможен и другой путь. Обратимся к формулам индексов Ласпейреса (10.5) и Пааше (10.7). Этииндексы могут быть рассчитаны на основе данных о количестве проданных товаров в базисноми отчетном периоде (по каждому j-му товару) q0j и q1j и ценах – р1j и р0j. Такие индексыпринято называть агрегатными. Так же можно построить и Iq  не через осреднениеиндивидуальных индексов, а на основе сравнения двух сумм (агрегатов), см. (10.7).

Агрегатные индексы считаются основной формой индексов. Они выполняют две функции:синтетическую и аналитическую. Первая функция обеспечивается тем, что в одном индексеобобщаются (синтезируются) непосредственно несоизмеримые явления. Например, цены наразные товары или разные товары, абсолютно не сопоставимые между собой в натуральномвыражении. Когда мы записываем

                        ,

то благодаря использованию ценового соизмерителя можно агрегировать данные по различнымтоварам.

Вторая функция - аналитическая - следует из взаимосвязи индексов. Дело в том, чтопрактически каждый индекс можно рассматривать как составляющую некоей системыиндексов, в которой его роль сводится к измерению одного из факторов общего изменениясложного явления и вклада этого фактора в совокупное изменение. Так, например, индекс ценможно рассматривать как показатель влияния изменения цен на выручку от продажи

55)

При изучении динамики коммерческой деятельности приходится производить индексные сопоставления более чем за два периода.

Поэтому индексные величины могут определяться как на постоянной, так и на переменной базах сравнения. При этом, если задача анализа состоит в получении характеристик изменения изучаемого явления во всех последующих периодах по сравнению с начальным, то вычисляются базисные индексы. Например, сопоставление объёма розничного товарооборота II, III и IV кварталов с I кварталом.

Но если требуется охарактеризовать последовательно изменения изучаемого явления из периода в период, то вычисляются цепные индексы. Например, при изучении объёма розничного товарооборота по кварталам года сопоставляют товарооборот II квартала c I, III — cо II и    IV — с III кварталом.

В зависимости от задачи исследования и характера исходной информации базисные и цепные индексы исчисляются как индивидуальные, так и общие.  Способы расчёта индивидуальных базисных и цепных индексов аналогичны расчёту относительных величин динамики. Общие индексы в зависимости от их вида вычисляются с переменными и постоянными весами — соизмерителями.

Используя индексный ряд за несколько периодов, можно получить динамику стоимости продукции и динамику товарооборота в неизменных ценах, т.е. в ценах какого - то одного прошлого периода. Такие индексные ряды называются индексами с постоянными весами. Для них действует правило: произведение цепных индексов даёт индекс базисный.

Если индексы цен, себестоимости и производительности труда имеют в качестве весов количество продукции отчётного периода, то эти индексы образуют индексные ряды с переменными весами, поскольку в каждом отдельном индексе отчётный период изменяется. Индексы с переменными весами не подчиняются правилу, согласно которому произведение цепных индексов равно базисному.

Индексы постоянного и переменного состава, индексы структурных сдвигов.

Изменение средней величины показателя зависит от двух факторов – изменения значения индексируемого показателя у отдельных единиц и изменения структуры явления.

Изменение структуры – это изменение доли отдельных групп единиц совокупности в общей их численности. Задача определения влияния каждого фактора определяется с помощью индексного метода, т.е. путем построения системы взаимосвязанных индексов, в которую включаются три индекса: переменного состава, постоянного состава и структурных сдвигов.

Индекс переменного состава – индекс, выражающий соотношение средних уровней изучаемого явления, относящихся в разным периодам времени. Например, индекс переменного состава себестоимости продукции:

.

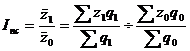Отражает изменение не только изменение индексируемой величины (в данном случае, себестоимости), но и структуры совокупности весов (объем).

Индекс постоянного состава – это индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины. Например, индекс фиксированного состава себестоимости продукции:

Индекс структурных сдвигов – индекс, характеризующий влияние изменения структуры изучаемого явления на динамику среднего уровня этого явления:

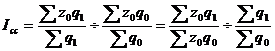
Система взаимосвязанных индексов при анализе динамики средней себестоимости имеет следующий вид:

56) Выборочное наблюдение относится к разновидности  несплошного наблюдения. Оно охватывает отобранную часть единиц генеральной совокупности. Цель выборочного наблюдения - по отобранной части единиц дать характеристику всей совокупности единиц. Чтобы отобранная часть была репрезентативна (т.е. представляла всю совокупность единиц), выборочное наблюдение должно быть специально организовано. Следовательно, в отличие от генеральной совокупности, представляющей всю совокупность исследуемых единиц, выборочная совокупность представляет ту часть единиц генеральной совокупности, которая является объектом непосредственного наблюдения.

По понятным причинам выборочный метод может широко использоваться органами государственной статистики. Он позволяет при значительной экономии средств и затрат получать необходимую достоверную информацию. Гарантия репрезентативности обеспечивается применением научно обоснованных способов отбора единиц, которые подлежат обследованию.

Следует сразу же иметь в виду, что при сопоставлении показателей по результатам выборочного исследования с характеристиками для всей генеральной совокупности могут иметь место отклонения. Величина этих отклонений называется ошибкой наблюдения, которая может быть или  ошибкой регистрации (несовершенство технических условий), или  ошибкой репрезентативности (случайное или систематическое нарушение правил при отборе единиц).

В статистике приняты следующие условные обозначения:

N - объем генеральной совокупности;

п - объем выборочной совокупности;

 - средняя в генеральной совокупности;

 - средняя в выборочной совокупности;

р - доля единиц в генеральной совокупности;

w - доля единиц в выборочной совокупности;

 - генеральная дисперсия;

S² - выборочная дисперсия;

 - среднее квадратическое отклонение признака в генеральной совокупности;

S - среднее квадратическое отклонение признака в выборочной совокупности.

Конец формы

Выборочные наблюдения. Принципы выборочного наблюдения.  Характеристика генеральной и выборочной совокупности. Ошибки: выборки, регистрации, репрезентативности, систематические, случайные

Выборочное наблюдение – это такое несплошное наблюдение, при котором статистическому обследованию подвергаются единицы совокупности, отобранные случайным способом. Задача такого наблюдения – по обследуемой части дать характеристику всей совокупности.

Выборочное исследование широко применяется на практике, поскольку обладает существенными преимуществами по сравнению с другими методами получения статистических данных. К ним относятся:

• Достаточно высокая точность результатов обследования благодаря использованию более квалифицированных кадров, что приводит к сокращению ошибок регистрации;

• Экономия времени и средств в результате сокращения объема работы, большая оперативность в получении данных о результатах обследования;

• Возможность исследования очень больших статистических совокупностей;

• Выборочный метод является единственно возможным, если сбор информации связан с разрушением или потерей единиц наблюдения, например, при органалитическом контроле качества продукции;

• Возможность исследования полностью недоступных совокупностей.

При выборочном исследовании изучается сравнительно небольшая часть статистической совокупности (5-10%, реже 20-25% объема ее единиц).

Проведение выборочного исследования является достаточно сложным процессом, выполнение которого включает в себя:

• обоснование целесообразности применения выборочного метода в данном исследовании;

• составление программы исследования;

• установление объема выборки – n;

• обоснование способа формирования выборки;

• отбор единиц из Генеральной совокупности (формирование выборки);

• измерение изучаемых признаков у отдельных единиц;

• обработка полученной информации и расчет характеристик выборки;

• определение ошибки выборки;

• распространение выборочных характеристик на Генеральную совокупность.

Для постановки задачи выборочного исследования необходимо ввести следующие понятия:

- Генеральная совокупность – изучаемая совокупность, из которой производится отбор единиц, подлежащих изучению, она может быть конечной (N) или бесконечной (∞).

- Выборочная совокупность (выборка) – часть единиц генеральной совокупности, отобранная для изучения (n). Обозначим показатели, характеризующие выборочную и генеральную совокупности:

№ п/п	Характеристики	Генеральная совокупность	Выборочная совокупность
1	2	3	4
1	Объем совокупности	N	n
2	Численность единиц, обладающих исследуемым свойством	М	m
3	Доли, единицы, обладающие исследуемым свойством
4	Средняя величина
5	Дисперсия

Эти ошибки называются ошибками выборки, т.к. значения, отобранные в выборку являются случайными, следовательно, ошибки в выборке являются также случайными.

 – число;   – интервал.

Разность между генеральной средней и выборочной средней   может оцениваться   – средняя ошибка,   – предельная ошибка. Средняя ( ) ошибка является стандартной ошибкой является точечной величиной, которая выражается одним числом, а именно средним квадратическим отклонением от математического ожидания выборочной средней и рассчитывается в  :  ,  ,  .

Предельная ошибка выборки определяет границы, в пределах которых лежит генеральная средняя, т.е. предельная ошибка является   интервальной:

       

     

Используются специальные обозначения (см.таблицу выше) и ошибка лежит в интервале:  .

При правильном формировании выборки величину ее ошибки можно рассчитать заранее. В общем случаепод ошибкой выборки понимают объективно возникающее расхождение между характеристикам выборки и генеральной совокупности.

Ошибки выборки подразделяются на ошибки регистрации и ошибки репрезентативности.

Ошибки регистрации возникают из-за неправильных или неточных сведений. Их источником является невнимательность регистратора, неправильное заполнение формуляров, описки или же непонимание существа исследуемого вопроса.

Ошибки репрезентативности возникают вследствие несоответствия структуры выборки структуре генеральной совокупности. Источником их существования является разная вариация признака у статистических единиц, в результате которой распределение единиц в выборочной совокупности отличается от распределения единиц в генеральной совокупности. Ошибки репрезентативности делятся на систематические и случайные.

Систематические ошибки репрезентативности возникают из-за неправильного формирования выборки, при котором нарушается основной принцип научно организационной выборки – принцип случайности.

Случайные ошибки репрезентативности означают, что даже при соблюдении принципа случайности отбора единиц, расхождения между характеристиками выборки и генеральной совокупности все же имеют место.

При использовании выборочного метода достоверность генеральных параметров (параметров генеральной совокупности) прежде всего зависит от репрезентативности выборки, т.е. от того, на сколько полно и адекватно представлена в выборке (n) генеральная совокупность (N).

Единицы отбираются в выборку случайным образом, а следовательно ошибки также случайны.

Выделяют ошибки:

А) средняя ошибка  ;

Б) предельная ошибка  ;

Для средней	Для доли
Повторный отбор
Бесповторный отбор

Предельная ошибка выборки  – определяет границы в пределах, которых будет лежать генеральная средняя  :                                                                 

Таблица Лапласа

p	0,683	0,954[1]	0,997
t	1,0	2,0	3,0

где p – вероятность, а t – коэффициент доверия или кратности.

В математической статистике доказано, что предельная ошибка является кратной средней ошибкой с коэффициентом кратности t, значение которого зависит от доверительной вероятности p по таблице Лапласа.

t – еще называют в некоторых учебниках коэффициентом доверия.

Однократная будет всегда 68,3%.

р – доверительная вероятность, еще называют уровнем надежности.

Пример: Для определения срока (средней) пользования краткосрочным кредитом в банке была произведена 5% механическая выборка, в которой попало 100 счетов. В результате обследования выборки установлено, что средний срок пользования краткосрочным кредитом составляет 30 дней, при средне квадратическом отклонении 9 дней. В 5-ти счетах из 100 срок пользования кредитом превысил 60 дней с вероятностью 0,954 (р=0,954, t=2) определить пределы, в которых будет находиться срок пользования краткосрочным кредитом по банку в целом, а также долю счетов со сроком пользования краткосрочным кредитом более 60 дней.