Расчет индексов сезонности в Excel.

Рассчитать индексы сезонности можно двумя способами.

Если в течении года присутствовала ярко выраженная тенденция (тренд) роста или объемов продаж, применяется формула: 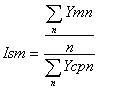    , где

I_sm – индекс сезонности месяца m

Y_mn – значение объема реализации за месяц m, года n;

Y_cpn – среднемесячный объем реализации за год;

N – количество анализируемых лет.

Иначе говоря, прогнозируемый на месяц m индекс сезонности равен среднему индексу сезонности для этого месяца за n лет.

Если в течение года ярко выраженной тенденции (тренда) роста или спада объемов продаж нет, применяется формула:   .

Иначе говоря, прогнозируемый на месяц m индекс сезонности равен отношению среднего значения объема продаж за несколько лет, за указанный месяц к среднемесячному объему продаж товара за n лет.

На рисунке 1 представлена таблица со статистикой продаж товара за четыре года по месяцам и индексы сезонности. Is1 – индекс сезонности рассчитанный первым способом, Is2 – индекс сезонности рассчитанный вторым способом.

Расчет промежуточных результатов осуществлен с помощью следующих формул:

Столбец F («всего») – простое суммирование объемов реализации за указанный месяц по годам: =СУММ(В4:Е4). 

Столбец G («в среднем») – отношение объема реализации за все годы к количеству лет: =F4/СЧЕТ(В4:Е4).

Для расчета индекса сезонности первым способом первоначально необходимо рассчитать индексы сезонности для каждого года раздельно. В таблице индексы сезонности по годам рассчитываются в столбцах Н-К. расчетная формула имеет вид (для января 2001 года): =В4/(16/12)*100. И, наконец, индекс Is1 рассчитывается как среднее значение индексов по годам: =СРЗНАЧ(Н4:К4).

Для расчета индекса сезонности вторым способом необходим средний объем продаж за месяц по годам. Он уже рассчитан в столбце G. Среднемесячный объем продаж за все годы рассчитан рассчитывается в ячейке «G16» по формуле: СУММ(G4:G15)/12. то есть сумма средних объемов продаж по каждому месяцу делится на количество месяцев. И последний шаг – делим средний объем продаж за месяц m на среднемесячный объем продаж за четыре года: =G4/16*16.

50) Модели, учитывающие сезонность

Сезонность можно учитывать, создавая модель временного ряда.

Эти ряды и их колебания можно представить как генерируемые моделями двух основных типов: моделями с мультипликативными и с аддитивными коэффициентами сезонности.

Модели первого типа имеют вид:

,

где динамика величины   характеризует тенденцию развития процесса;

,  ,...,   — коэффициенты сезонности;

 — количество фаз в полном сезонном цикле (если ряд представляет месячные наблюдения, то в экономике обычно   = 12, при квартальных данных   = 4 и т. п.);

 — неавтокоррелированный шум с нулевым математическим ожиданием.

Модели второго типа записываются как:

,

где величина   описывает тенденцию развития процесса;

,  ,...,   — аддитивные коэффициенты сезонности;

 — количество фаз в полном сезонном цикле;

 — неавтокоррелированный шум с нулевым математическим ожиданием.

Адаптивная модель с мультипликативной сезонностью была предложена П. Р. Уинтерсом. Аддитивная модель рассмотрена Г. Тейлом и С. Вейджем. Уинтерс поставил задачу разработать модель для прогнозирования объемов сезонных продаж с использованием ЭВМ. Модель должна быть такой, чтобы: а) прогнозы рассчитывались на основе одних и тех же программ для большого количества продуктов; б) вычисления производились быстро и дешево; в) использовался минимальный объем памяти для информации; г) учитывались изменяющиеся условия. Поэтому целесообразно в прогностических моделях учитывать конкретный характер тенденции и сезонных колебаний. Это и сделал Уинтерс с помощью экспоненциальной схемы. Модель при этом становится сложнее, зато и точность прогнозов для большинства товаров существенно возрастает.