- •1. Внешние и внутренние силы. Применение метода сечения для определения внутренних сил и напряжений
- •4. Расчёт на прочность при растяжении и сжатии. Допускаемое напряжение и коэффициент запаса.
- •5. Потенциальная энергия упругой деформации
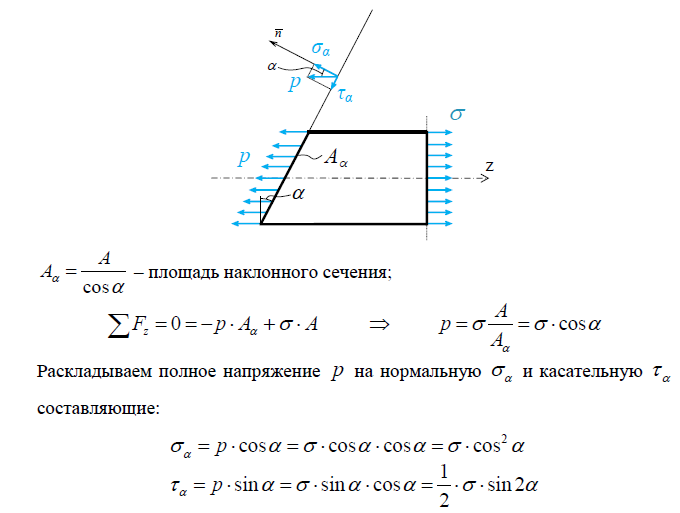
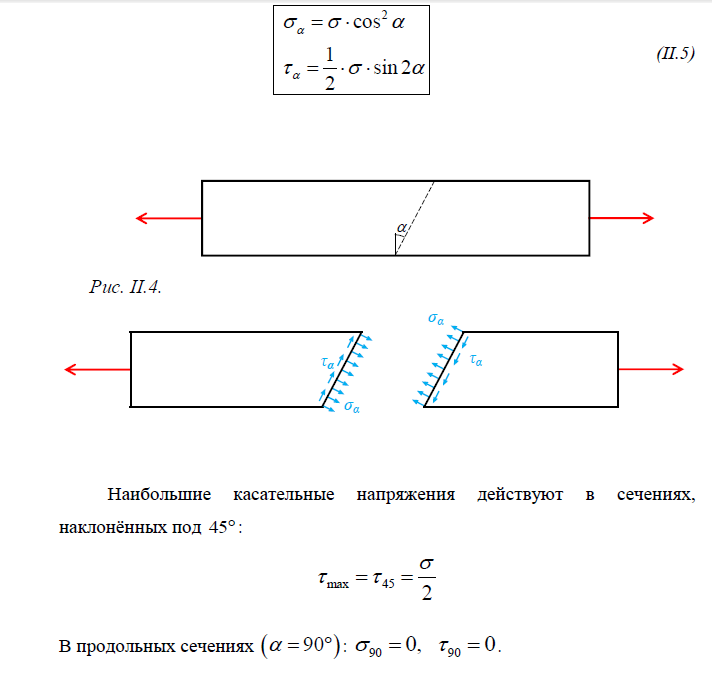
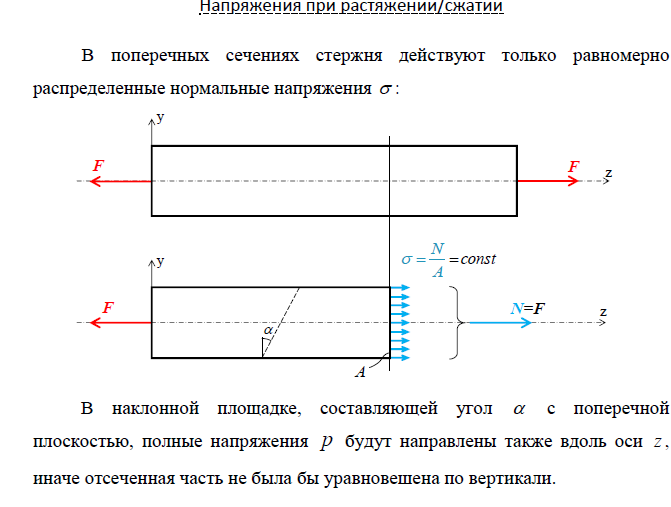
- •6 Напряжения по наклонным сечениям при осевом растяжении или сжатии
- •Чистый сдвиг
- •9. Напряженные состояния
- •Главные напряжения и главные площадки
- •11. Обобщенный закон Гука. Деформация при плоском и объемном напряжении состояния.
- •12. Теории прочности
- •13. Напряжение в брусе при поперечном изгибе
- •14.Геометрические характеристики плоских сечений
- •Просуммировав (проинтегрировав) такие произведения по всей площади фигуры, получаем статические моменты относительно осей y и X: ; [см3, м3, т.Д.].
- •Моменты инерции плоских сечений.
- •Свойства аддиативности моментов инерции.
- •Изменение моментов инерции при параллельном переносе осей координат.
- •15. Зависимость между моментами инерции при повороте осей:
- •Замечание. Геометрические характеристики сечений, координаты центров тяжести сечений относительно начальных и центральных осей целесообразно оформить в виде таблицы (см. Пример расчета),
- •20. Нормальное напряжение при чистом изгибе.
- •Расчет на прочность при изгибе
- •21. Нормальные и касательные напряжения при поперечном изгибе
- •4.1. Дифференциальное уравнение изогнутой оси балки и его интегрирование.
- •26.Потенциальная энергия упругой деформации
- •30. Канонические уравнения метода сил
- •31.Косой изгиб
- •32. Ядро сечения
- •33. Кручение круглых валов
- •Внутренний крутящий момент
- •34. Определение критических сил для идеальных стержней при различном креплении концевых сечений
- •35. Критическое напряжение. Пределы применимости формулы эйлера
4. Расчёт на прочность при растяжении и сжатии. Допускаемое напряжение и коэффициент запаса. 8
5. Потенциальная энергия упругой деформации 9
6 НАПРЯЖЕНИЯ ПО НАКЛОННЫМ СЕЧЕНИЯМ ПРИ ОСЕВОМ РАСТЯЖЕНИИ ИЛИ СЖАТИИ 13
Главные напряжения и главные площадки 18
11. Обобщенный закон Гука. Деформация при плоском и объемном напряжении состояния. 19
12. Теории прочности 20
13. Напряжение в брусе при поперечном изгибе 20
Статический момент элемента площади dF относительно оси 0x — произведение элемента площади на расстояние "y" от оси 0x: dSx = ydF 21
Просуммировав (проинтегрировав) такие произведения по всей площади фигуры, получаем статические моменты относительно осей y и x: ; [см3, м3, т.д.]. 21
Моменты инерции плоских сечений. 22
Свойства аддиативности моментов инерции. 22
Изменение моментов инерции при параллельном переносе осей координат. 23
Замечание. Геометрические характеристики сечений, координаты центров тяжести сечений относительно начальных и центральных осей целесообразно оформить в виде таблицы (см. пример расчета), 26
6. Проводится контроль правильности определения координат центров тяжести сечения и его элементов. Для этого вычисляется статический момент сечения относительно центральных осей, которые при правильном расчете должны равняться нулю: 26
20. Нормальное напряжение при чистом изгибе. 35
Расчет на прочность при изгибе 37
21. Нормальные и касательные напряжения при поперечном изгибе 38
26.Потенциальная энергия упругой деформации 45
30. Канонические уравнения метода сил 48
31.Косой изгиб 50
32. Ядро сечения 50
33. Кручение круглых валов 51
35. КРИТИЧЕСКОЕ НАПРЯЖЕНИЕ. ПРЕДЕЛЫ ПРИМЕНИМОСТИ ФОРМУЛЫ ЭЙЛЕРА 56
1. Внешние и внутренние силы. Применение метода сечения для определения внутренних сил и напряжений
Под внешними силами понимаются силы, возникающие в результате взаимодействия рассматриваемого тела с окружающими телами.
Внутри любого материала имеются внутренние межатомные силы.
Приложение к телу внешней нагрузки вызывает изменение (увеличение или уменьшение) их, т.е. появление дополнительных внутренних сил. Дополнительные силы взаимодействия, возникающие внутри объекта под действием внешних сил, называются в сопротивлении материалов внутренними силами.Для определения внутренних усилий используется метод сечений.
Сущность метода заключается в следующем.
Пусть некоторое тело находится в равновесии под действием системы внешних сил
Рассечем (мысленно) тело на две части плоскостью, перпендикулярной продольной оси тела (поперечным сечением).
Отбросим правую или левую часть тела. Чтобы оставшаяся часть находилась в равновесии, по плоскости сечения должны действовать внутренние силы.
Заменим действие одной части на другую внутренними силами. Эти внутренние силы по характеру приложения - распределенные, в общем случае они не одинаковы по всему сечению.
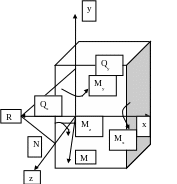
N - продольная (нормальная) сила, проекция вектора R на ось z;
Qx, Qy - поперечные силы, проекции вектора R на оси x, y соответственно;
Mz=Mк - крутящий момент, составляющая момента M вокруг оси z;
Mx, My - изгибающие моменты, составляющие момента M вокруг осей x, y соответственно.
Уравновесим отсеченную часть. Так как отсеченная часть тела находится в равновесии, то для определения шести неизвестных составим шесть уравнений равновесия:
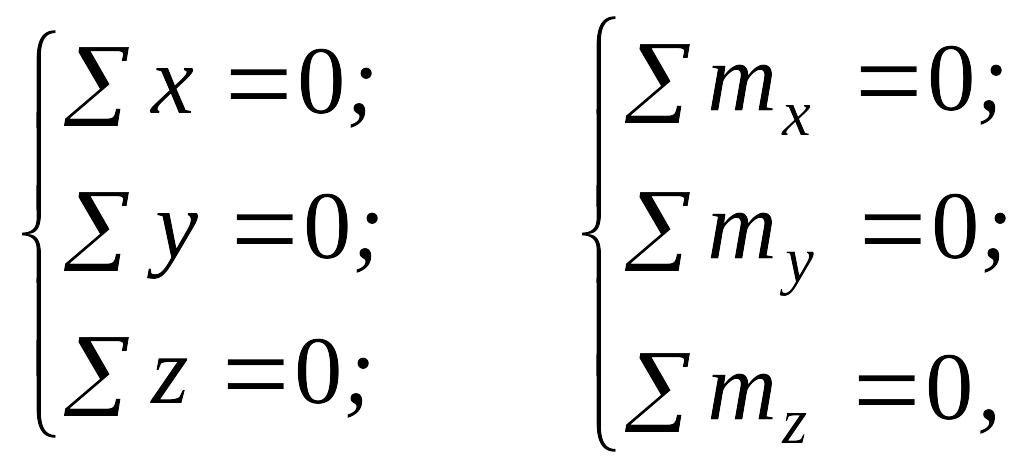
![]() -
нормальная сила
равна сумме проекций всех внешних сил,
-
нормальная сила
равна сумме проекций всех внешних сил,
действующих на отсеченную часть, на продольную ось z;
![]() -
поперечные силы
равны по величине суммам
-
поперечные силы
равны по величине суммам
проекций всех внешних сил, действующих на отсеченную часть, на оси x и y соответственно;
![]() -
крутящий момент
равен сумме внешних моментов, действующих
на отсеченную часть, относительно оси
z;
-
крутящий момент
равен сумме внешних моментов, действующих
на отсеченную часть, относительно оси
z;
![]() ;
;
![]() -
изгибающие моменты
равны суммам внешних моментов, действующих
на отсеченную часть, относительно осей
х и
у
соответственно.
-
изгибающие моменты
равны суммам внешних моментов, действующих
на отсеченную часть, относительно осей
х и
у
соответственно.
Понятие о напряжениях, деформациях и перемещениях. Нормальные и касательные напряжения. Вектор полного перемещения. Линейная и угловая деформация
Напряжение – численная мера распределения внутренних сил по плоскости поперечного сечения. Его используют при исследовании и определении внутренних сил любой конструкции.
Выделим на плоскости сечения площадку A; по этой площадке будет действовать внутренняя сила R (рис. I.1.10а).
Величина отношения R/A=pсрназывается средним напряжением на площадке A. Истинное напряжение в точке А получим устремив A к нулю:
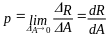
Нормальные напряжения возникают, когда частицы материала стремятся отдалиться друг от друга или, наоборот, сблизиться. Касательные напряжения связаны со сдвигом частиц по плоскости рассматриваемого сечения.
Очевидно, что
![]() .
Касательное напряжение в свою очередь
может быть разложено по направлениям
осей x
и y
(tzх,
tzу).
Размерность напряжений – Н/м2
(Па).
.
Касательное напряжение в свою очередь
может быть разложено по направлениям
осей x
и y
(tzх,
tzу).
Размерность напряжений – Н/м2
(Па).
При действии внешних сил наряду с возникновением напряжений происходит изменение объема тела и его формы, т. е. тело деформируется. При этом различают начальное (недеформированное) и конечное (деформированное) состояния тела.
Отнесем недеформированное тело к декартовой системе координат Oxyz. Положение некоторой точки М в этой системе координат определяется радиус-вектором r(х, у, z). В деформированном состоянии точка М займет новое положение М/ , характеризуемое радиус-вектором r' (х, у, z). Вектор u=r'—r называется вектором, перемещений точки М.
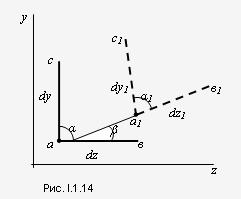
Под действием внешних сил
любое тело деформируется, т.е. его
форма и размеры изменяются, а точки тела
меняют положение в пространстве. Пусть
имеется тело с приложенными к нему
силами Рi.
Мысленно через точку а
в направлениях осей у
и z
проведем бесконечномалые отрезки ав
иас,
длины которых dy
и dz.
После деформации бруса отрезки примут
положение, изображенное штриховой
линией (рис. I.1.14). Точка а
переместится в положение а1.
Величина аа1,
равная изменению координат точки
называется линейным
перемещением точки
а.
Отрезки ав
и ас
займут новые положения а1в1
и а1с1.
Их длины изменяются на Δdy
и Δdz
и называются абсолютными
линейными деформациями.
Угол между начальным положением отрезка
ав
и конечным - а1в1
- называются угловым
перемещением b.
Линейные перемещения измеряются в
единицах длины, угловые - в радианах или
градусах. Отношение приращения длины
отрезка к его начальной длине представляет
собой относительную
линейную деформацию,
т.е.
![]() .
Аналогично
.
Аналогично
![]() .
.
Линейные деформации
величины безразмерные. Изменение
первоначально угла между отрезками ав
и ас
после приложения к телу нагрузки,
выраженное в радианах, представляет
собой угловую
деформацию![]() .
.
Совокупность линейных деформаций e по различным направлениям и угловых деформаций g по различным плоскостям, проходящим через рассматриваемую точку, представляет собой деформированное состояние в этой точке.
2. Гипотеза сплошности и однородности: материал представляет
собой однородную сплошную среду; свойства материала во всех точках тела одинаковы и не зависят от размеров тела
Гипотеза сплошности. Жидкость рассматривается как деформируемая система материальных частиц, непрерывно заполняющих пространство, в котором она движется.
Жидкая частица представляет собой бесконечно малый объем, в котором находится достаточно много молекул жидкости. Например, если рассмотреть кубик воды со сторонами размером 0,001 см, то в объеме будет находиться 3,3-1013 молекул. Частица жидкости полагается достаточно малой по сравнению с размерами области, занятой движущейся жидкостью.
При таком предположении жидкость в целом рассматривается как континуум - сплошная среда, непрерывно заполняющая пространство, т.е. принимается, что в жидкости нет пустот или разрывов, все характеристики жидкости являются непрерывными функциями, имеющими непрерывные частные производные по всем своим аргументам. Сплошная среда представляет собой модель, которая успешно используется при исследовании закономерностей покоя и движения жидкости.
Правомерность применения модели жидкости - сплошная среда подтверждена всей практикой гидравлики.
![]()


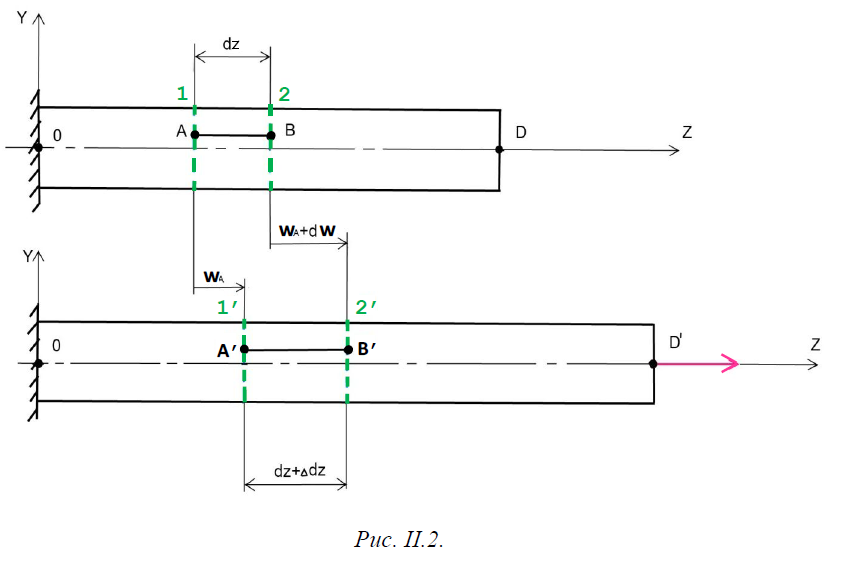
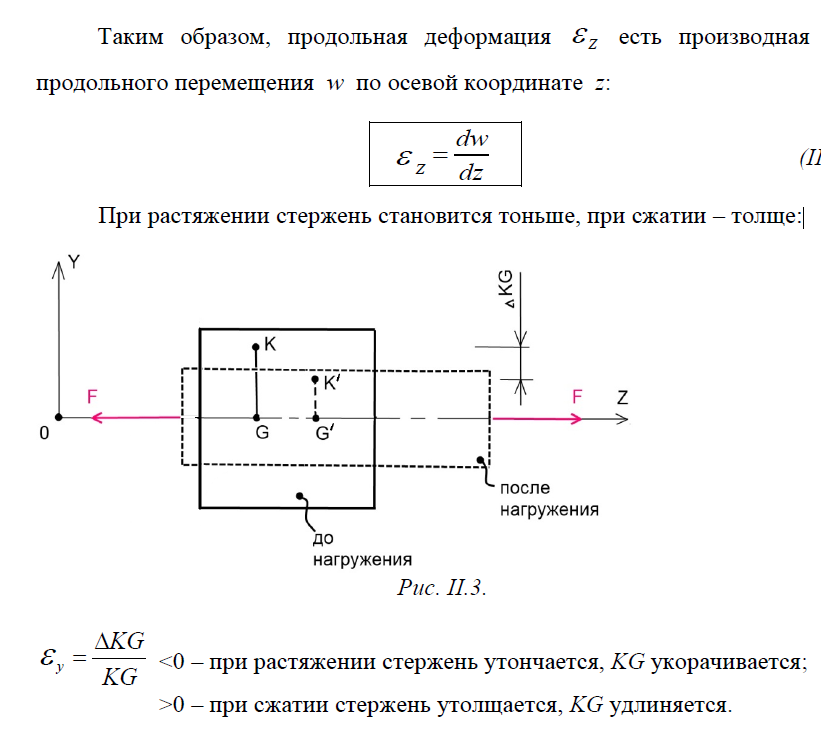
3. Перемещения и деформации при растяжении (сжатии)
При растяжении и при сжатии стержня перемещения его точек возможны лишь вдоль оси Оz. Обозначаются эти перемещения w и имеют размерность [м].


 6
6