2. Множества и операции над ними

В современной математике понятие множества считается одним из основных или неопределяемых. Так или иначе, с него начинается изложение традиционных математических дисциплин и построение новых математических теорий, возникающих по мере того, как расширяется сфера применений математики. "Множество - есть многое, мыслимое как единое "- сказал один из основателей Теории множеств Георг Кантор. "Множество- набор, совокупность, собрание, ансамбль и т.д. каких- либо объектов произвольной природы". Эти утверждения не являются в полном смысле логическим определением понятия "множество", а лишь поясняют его смысл.

Множества обозначаются заглавными латинскими буквами: А,В,С,...,Z. Например, А=h;k;n;x Множество А состоит из букв латинского алфавита h,k,n,x.

Предметы любой природы, составляющие множество, называются элементами множества. Взаимосвязь между множеством и его элементами может быть выражена при помощи слов принадлежит, не принадлежит, содержится не содержится, входит не входит, является элементом не является элементом. Например, х А, yА читается : в множество А входит элемент х; у не принадлежит множеству А. Множество может содержать один, два, несколько элементов или не содержать вообще элементов. Множество, не содержащее ни одного элемента, называется пустым. Пустое множество обозначается . По числу элементов множество может быть конечным и бесконечным. Определить множество (или задать) это значит относительно любого предмета уметь ответить на вопрос: принадлежит он данному множеству или нет. Множество может быть задано двумя способами. 1) Перечислением всех его элементов. Например, множество Х состоит из чисел 2,4,6,8,10 можно задать так: Х=2,4,6,8,10. 2)Характеристическим свойством. Характеристическое свойство - это такое свойство, которым обладают все элементы данного множества и не обладают ни один, не принадлежащий этому множеству. Например, множество В- натуральных чисел, меньших 8, можно символически записать В=х  хN, х8 . Если указать все элементы множества В, то получится В=1,2,3,4,5,6,7. Если каждый элемент множества В является элементом множества А, то говорят, что множество В является подмножеством множества А и пишут ВА.

Н аглядно отношение между множествами можно показать при помощи особых чертежей, называемых кругами Эйлера или диаграммами Венна

А

ВА

Например, А - множество воспитанников детского сада №5, В- множество воспитанников старшей группы детского сада №5. В является подмножеством множества А, т.е. ВА. Считают, что  множество является подмножеством любого множества. Если для какого- либо множества U рассматривают только подмножества, то множество U называют универсальным. Например, для множеств А- простых чисел, В- составных чисел, С- четных чисел множество натуральных чисел N является универсальным, т.к. АU, ВU, СU. На кругах Эйлера это будет изображено так:

Рис.1 Рис.2

Два множества А и В называют равными, если они состоят из одних и тех же элементов и пишут А=В. На кругах Эйлера равные множества обозначают так: А В

И з двух или более множеств в результате выполнения операций пересечения, объединения, вычитания, декартова произведения образуют новые множества. Пересечением множеств А и В называется множество А  В, содержащее те и только те элементы, которые одновременно входят в оба множества А и В. На кругах Эйлера изображают заштрихованной областью: А В

Например, пересечением множеств А=а,в,с,d,e,f и В=b,d,e,g,h является множество АВ=в,d,e, т.к. ему принадлежат элементы, входящие в оба множества и А и В.

О бъединением множеств А и В называется множество АВ, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств А или В. На кругах Эйлера изображают заштрихованной областью: А В

Например, объединением множеств, рассмотренных в предыдущем

примере, является множество АВ=а,в,с,d,е,f,g,h, т.к. ему принадлежат элементы, входящие хотя в одно из множеств А или В.

Разностью множеств А и В называется множество А \ В, в которое входят все элементы из А, не принадлежащие В. В случае, когда ВА, множество А\В называют дополнением множества В до множества А и обозначают В'. На кругах Эйлера изображают так:

В'А А \ В

А

В

Пример1.Разностью множеств А=2,4,6,8,10 и В=1,2,3,4,5,6 является множество А \ В=8,10, т.к. оно состоит из элементов входящих в множество А, но не входящих в множество В. Пример2. Дополнением множества В=ц,у,к до множества А=н,е,у,ц,к,г является множество В'=н,е,г, т.к. множество ВА и В' состоит из элементов, входящих в множество А, но не входящих в множество В. Декартовым произведением множеств А и В называют множество АхВ пар (а,в), первая координата а которых принадлежит множеству А, а вторая координата в принадлежит множеству В. Например, декартовым произведением множеств А=1,2,3 и В=а,в является множество А х В=(1,а); (1,в); (2,а); (2,в); (3,а); (3,в) Соответствием между элементами двух множеств Х и У называют всякое подмножество декартова произведения множества Х и У. Соответствия обозначают латинскими буквами R,P,S,T и т.д. Например, задано соответствие R "число х из множества Х делится на число у из множества У" между элементами множества Х=5,6,7,8,9 и У=2,3. Соответствие R будет представлять собой множество пар (х,у), таких, что "х делится на у". R=(6,2); (8,2); (6,3); 9,3)

Соответствие между элементами множества удобно изображать с помощью особых чертежей - графов. В них множества показаны с помощью кругов Эйлера, элементы - точками, взаимосвязь между множествами- стрелками, идущими от элементов множества Х к элементам множества У. Например, граф соответствия R, рассмотренного выше будет иметь вид:

.5
.6	.2
.7
.8	.3
.9

Это же соответствие можно задать с помощью таблицы:

У \ Х	5	6	7	8	9
2		+		+
3		+			+

каждая пара (х,у) соответствия будет изображена точкой в прямоугольной системе координат.

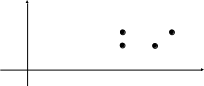у

0 1 2 3 4 5 6 7 8 9 10 х Соответствие между множествами Х и У называется взаимно однозначным, если каждому элементу множества Х соответствует единственный элемент множества У и каждый элемент множества У соответствует только одному элементу множества Х. Например, соответствие P: "Каждому слову х соответствует его первая буква у", заданное между множествами Х=ручка, парта, дневник, школа и У=д,п,р,ш является взаимно однозначным, т.к. каждому слову из множества Х соответствует единственная буква из множества У и наоборот. На графе взаимно однозначного соответствия от всех элементов множества Х идут по одной стрелки и нет свободных элементов в множестве У.