25. Теорема Хана-Банаха о продолжении линейного функционала (с док-вом). Следствия.
Теорема
(о продолжении линейного функционала).
Пусть на конечном пространстве
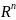определенна функция
,
которая является выпуклой и
положительно-однородной, т.е.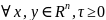
выполнены
соотношения:
.
Пусть также L
линейное подпространство в
на
котором определена линейная функция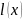
такая, что
.
Тогда существует линейная функция
(«продолжение
»),
определенная на всем пространстве
,
которая совпадает с исходной
на подпространстве
и мажорируется функцией
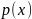уже на всем
,
т.е.
Док-во:
Если
совпадает со всем
,
то док-ть нечего
Если это не так, то
Рассмотрим пару произвольных точек
х,у
поэтому получаем следующее соотношение
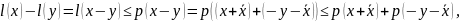которые
можно переписать в виде след-щего нер-ва:
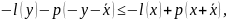выполненного
для любой пары х,у
.
Из неравенства (а) выводим:
Аналогичные
действия проделываем с нер-вом(б).
Итак,
функция ℓ(.)
была продолжена с исходного линейного
подпространства L
на
линейное подпространство большей
размерности с сохранением верхней
оценки значениями выпуклой
положительно-однородной функции p(x).
Очевидно,
что либо
либо
указанную процедуру продолжения линейной
функции можно повторить. В итоге,
благодаря конечной размерности
пространства
за
конечное число “продолжений” будет
построена требуемая линейная функция,
определенная на всем
Теорема
доказана.
26. Принцип сжимающих отображений (с док-ом) и его применение.
Принцип Сжимающих отображений: Сжимающее отображение метрического пространства в себя имеет неподвижную точку, и притом только одну.
27. Интегральные уравнения Вольтерра второго рода. Представление решения через резольвенту ядра.
Интегральные
уравнения – уравнения, содержащие
неизвестную функцию под знаком интеграла.
Ур-ия 1-го и 2-го рода с пост-ми пределами
интегрирования наз-ся ур-ми Фретгольма,
а ур-ния с переменным верхним пределом
наз-ся ур-ми Вольтерра. Линейное инт-ое
ур-ние Вольтерра первого рода имеет
вид:
Линейное
инт-ое ур-ние Вольтерра второго рода:
.
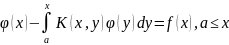Здесь
-
неизвестная искомая ф-ция;
– заданная непрерывная ф-ция, называемая
свободным членом интегрального ур-ния;
- заданная непрерывная ф-ция, называемая
ядром интегрального ур-ния . Ур-ния
второго рода иногда записывают с
параметром
:
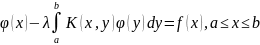или
.
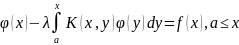Теорема
(метод резольвент для уравнения Вольтерра
второго рода): пусть
ядро k(t,
s)
и свободный член f
(t)
уравнения
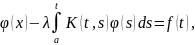квадратично
суммируемы, тогда при любом
это
уравнение имеет единственное суммируемое
решение
,
которое может быть получено, как сумма
ряда Неймана
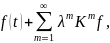
где
Замечание:
с
помощью резольвенты решение интегрального
уравнения Вольтерра второго рода
записывается в виде
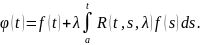
28. Спектр оператора в Банаховом пространстве. Резольвента. Аналитические свойства резольвенты.
Пусть
A - ограниченный оператор. Рассмотрим
оператор A −
λI.
Спектром оператора называется множество
точек λ ∈
C,
для которых не существует ограниченного
обратного оператора к A −
λI.
Мы будем обозначать спектр
оператора A через
(A).
Точки, лежащие в дополнении к спектру, называются регулярными.
Пусть
A: X →
X
– ограниченный оператор. Резольвентой
оператора называется функция
Обратим
внимание на то, что
(когда
сущ-ет), а существование и непрерывность
оператора
зависят от поведения резольвенты
при
.
В точках спектра резольвента либо не существует, либо не определенна на всем пространстве Х.
Лемма 4.1 (Тождество Гильберта). Для резольвенты оператора A имеет место формула R(z) − R(w) = (z − w)R(z)R(w).
Рассмотрим тождество (A − wI) − (A − zI) = (z − w)I. Домножим слева на оператор R(z), а справа на R(w), получим
R(z)(A − wI)R(w) − R(z)(A − zI)R(w) = R(z)(z − w)R(w). После сокращения прямых и обратных операторов получим R(z) − R(w) = (z − w)R(z)R(w).