Глава 1. Основные понятия и показатели надежности экономических информационных систем

1.1. Основные понятия и определения

В настоящее время в теории надежности существует единая установившаяся терминология, которая охватывает важнейшие понятия и определения. Основные понятия теории надежности изложены в ряде стандартов [23 - 28]. Надежность системы является одной из основных составляющих его качества. Дадим определения понятиям согласно ГОСТа по надежности. Качество - совокупность свойств продукции, которая позволяет оценить пригодность продукции удовлетворять определенным потребностям в соответствии с её назначением (рис 1.1).

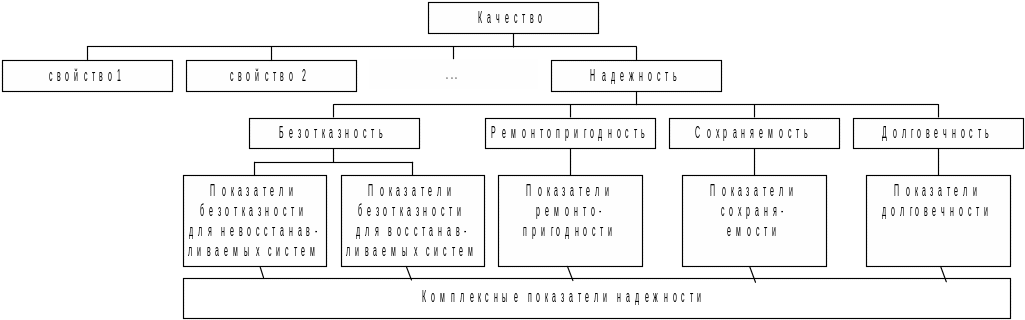
Рис. 1.1. Структура свойств качества и надежности

Одним из качеств изделия является надежность - особое свойство, которое позволяет определить стабильность всех других свойств качества изделия во времени. Свойство - объективная особенность изделия, которое проявляется при его создании, эксплуатации и потреблении. Надежность системы (согласно ГОСТа 27.002-89) - свойство системы выполнять заданные функции, сохраняя свои эксплуатационные показатели в заданных пределах в течение требуемого промежутка времени или требуемой наработки. Исправное состояние - состояние, при котором система обладает полным набором свойств и выполняет все заданные функции с параметрами, установленными в технической документации. Работоспособность - состояние, при котором система выполняет все заданные функции с параметрами, установленными требованиями технической документации, но с отсутствием некоторых несущественных для нормального функционирования свойств. Отказ - событие, которое заключается в нарушении работоспособности. Следует отметить, что под отказом надо понимать не только полное нарушение работоспособности, но и выход параметров изделия за границы, установленные требованиями технической документации. Значит, после отказа система либо полностью прекращает свою работу, либо продолжает функционировать с пониженным качеством. Во многих случаях понятие отказа удобно подразделять на его виды в соответствии с классификационными признаками:

1. По характеру возникновения:

• Внезапные (катастрофические). Возникают в результате резкого (скачкообразного) изменения выходных показателей системы;

• Постепенные (параметрические). Образуются при постепенном снижении выходных параметров системы во времени и когда эти параметры пересекают критическое значение, считается, что отказ произошел.

2. По степени очевидности:

• Явные (очевидные). Явные отказы системы обнаруживаются при внешнем осмотре или включении системы;

• Скрытые (неочевидные). Выявляются инструментальными средствами.

3. По связи с отказами других элементов:

• Зависимые (вторичные отказы). Возникают под влиянием отказов других элементов;

• Независимые (первичные отказы).

4. По времени существования:

• Устойчивые (окончательные). Устраняются только в результате ремонта;

• Перемежающие отказы (самопроизвольно возникают и устраняются). Исчезают без вмешательства обслуживающего персонала (например, сбои ЭВМ).

5. По влиянию на ремонтопригодность:

• Неисправности. Устраняются путем мелкого ремонта;

• Аварии. Требуют длительного восстановления и больших ремонтных работ.

6. По природе возникновения:

• Физические. Проявляются в физическом нарушении работоспособности;

• Функциональные. Теряют способность системы выполнять некоторые или все функции (например, при отсутствии физического отказа ЭВМ может неправильно выполнять логические операции).

Надежность является комплексным свойством системы и включает в себя еще четыре других свойства (рис 1.2):

1. Безотказность.

2. Долговечность.

3. Ремонтопригодность.

4. Сохраняемость.

1. Безотказность - свойство системы не утрачивать работоспособность в течение заданной наработки без перерывов.

2. Долговечность - свойство системы сохранять работоспособность до предельного состояния (до списания) с перерывами на техническое обслуживание и ремонт.

3. Ремонтопригодность - свойство системы обнаруживать, устранять и предупреждать неисправность и отказы путем проведения технического обслуживания и ремонта.

4. Сохраняемость - свойство системы сберегать свои эксплуатационные показатели в течение и после срока транспортирования или хранения на складе.

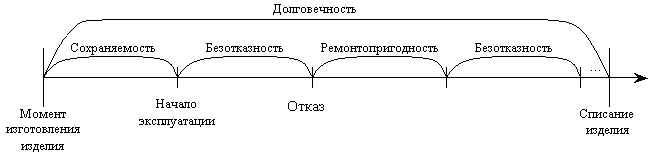
Рис. 1.2. Понятийная схема свойств надежности

Все системы подразделяются на восстанавливаемые и невосстанавливаемые. Невосстанавливаемые системы эксплуатируются до первого отказа. У восстанавливаемых систем может быть поток отказов. Кроме того, системы делятся на ремонтируемые и неремонтируемые. Это технические термины, говорящие о возможности ремонта системы. Так как ремонт может быть дорогой или в условиях эксплуатации не возможным, то система может быть ремонтируемой, но относится к классу невосстанавливаемых.

Понятия восстанавливаемых и невосстанавливаемых систем применяются для расчетов их надежности.

В связи с различными этапами жизненного цикла возникают специфические задачи обеспечения надежности ИС и используются соответствующие методы оценки надежности:

1. Этап проектирования. Схемно-конструктивные методы повышения надежности:

• Выбор и обоснование показателя эффективности ИС и определение его взаимосвязи с показателем надежности;

• Нормирование надежности. Определение оптимального уровня показателя надежности системы, которой она должна обладать во время эксплуатации системы;

• Расчет показателя надежности всей системы, если известны показатели надежности всех элементов;

• Решение задачи оптимального резервирования (дублирования отдельных элементов).

2. Этап изготовления. Производственные методы повышения надежности:

• Автоматизация технологических процессов;

• Методы статистического регулирования надежности;

• Тренировка элементов и систем (испытание сложной системы в течение небольшого промежутка времени с тем, чтобы выявить производственные дефекты).

3. Этап эксплуатации. Эксплуатационные методы повышения надежности:

   • Использование диагностических систем, которые выявляют скрытые дефекты;

   • Прогнозирование отказов системы.

Применение гибкой системы технического обслуживания и ремонта (ремонт производится в зависимости от состояния системы).

1.2. Система показателей надежности показатели безотказности, сохраняемости, ремонтопригодности, долговечности

Рассмотрим количественные показатели случайных величин, которые могут характеризовать свойства безотказности, ремонтопригодности, сохраняемости и долговечности. В качестве единиц измерения применяются:

- для безотказности - непрерывное время безотказной работы системы (наработка на отказ T’);

- для долговечности - время от момента изготовления системы до предельного состояния или списания. (срок службы T’’);

- для ремонтнопригодности - время восстановления работоспособности T’’’;

- для сохраняемости - случайное время сохранения работоспособности в состоянии хранения “T”.

Случайные величины, позволяют количественно оценить путем применения математического аппарата теории вероятностей и математической статистики. Полной характеристикой любой случайной величины является закон ее распределения, используемый в двух видах: как функция распределения (интегральный закон) и как плотность распределения (дифференциальный закон).

Функцией распределения называется функция F(t), определяющая вероятность того, что случайная величина Т примет значение, меньшее заданной величины t, т.е.:

.

Плотностью распределения вероятностей непрерывной случайной величины Т в диапазоне от 0 до бесконечности называют функцию f ( t ) - первую производную от функции распределения F ( t ):

.

В теории надежности широко используются еще две функции:

обратная функция распределения:

интенсивность:

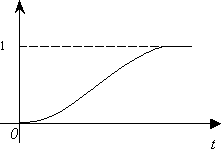
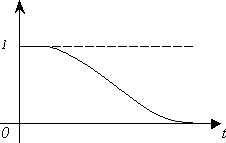
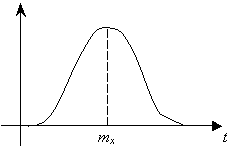
Рассмотрим графики этих функций.(рис. 1.3-1.6).

Рис.1.3. График функции Рис.1.4. График функции

Рис. 1.4. График функции Рис.1.5. График функции

Зависимость между функциями b(t) и можно определить из соотношений:

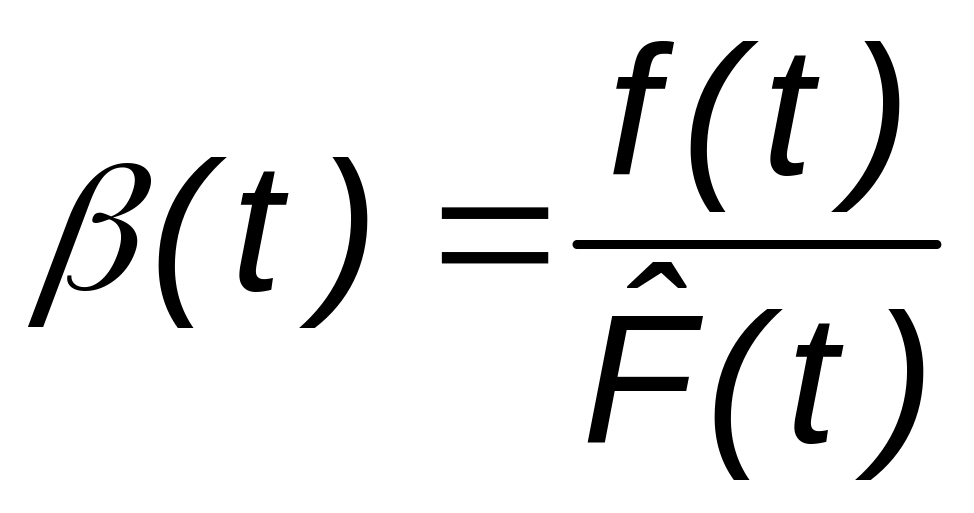, (1.2.5)

. (1.2.6)

Подставим выражение (1.2.6) в (1.2.5):

.

Проинтегрируем обе части выражения:

Таким образом, получаем зависимость от (t):

.