Филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования
«Уфимский Государственный Авиационный Технический Университет»
в г. Кумертау
Кафедра ЕН и ОТД
Лабораторная работа № 8
Изучение законов колебания маятников и связанных систем
Заведующий кафедрой ен и отд:
Проф. Даутов а.И.
Составил: Ст. Преподаватель
Медведев И.А.
Кумертау
2010
Изучение законов колебания маятников и связанных систем Приборы и принадлежности: 1. Установка (система маятников) 2. Штангенциркуль З. Рулетка 4. Секундомер. ЦЕЛЬ РАБОТЫ: 1 .Определение ускорения силы тяжести с помощью математического маятника. 2.Изучение зависимости между периодом колебаний и моментом инерции на примере физического маятника. З.Изучение колебаний связанных систем. ТЕОРИЯ МЕТОДА. Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости. Простейшими являются гармонические колебания, при которых колеблющаяся величина изменяется по закону синуса или косинуса. Этот вид колебаний представляет собой интерес по следующим причинам: во-первых, колебания в природе и технике часто имеют характер, очень близкий к гармоническим, и, во-вторых, периодические процессы любой формы (с другой зависимостью от времени) могут быть представлены как наложение нескольких гармонических колебаний. Примером гармонических колебаний может служить колебательное движение проекции точки, равномерного движущейся по окружности. Пусть точка В равномерно движется по окружности радиуса г с угловой скоростью ω (рис. 1), тогда уравнение гармонического колебательного движения проекции этой точки на ось Х будет иметь следующий вид:
Х=А
Sin
t
(Рис.1)
Или
X=A
Sin(2
/Т)
(1)
Здесь Х — смещение колеблющейся точки от положения равновесия,
А — амплитуда колебания, равная по величине радиусу окружности,
Т — период колебания,
— круговая
(циклическая) частота колеблющейся
точки, равная:
Где
- число колебаний в секунду.
=
- фаза колебания. Фаза колебаний определяет
положение колеблющейся точки от положения
равновесия, записывается в виде:
X=A
Sin
(
)
(2)
Здесь
фаза состоит из переменной части
и постоянной части
,
которая называется начальной фазой
колебания. В частном случае, если
=
/2,
уравнение смещения принимает вид:
X=A Cos
Скорость точки V при гармоническом колебании равна:
V=dx/dt=d/dt(A
Sin
=
A
Cos
(3)
Ускорение а при гармоническом колебании точки равно:
a=dV/dt=-
A
Sin
(4)
Знак минус говорит о том, что вектор ускорения направлен против вектора смещения.
Гармоническое колебание движения возникает под действием упругой и квазиупругой силы. Примером возникновения колебаний под действием упругой силы может служить идеальный пружинный маятник, у которого пружина абсолютно упруга и не имеет массы, т.е. вся масса маятника сосредоточена в его грузе (рис.2). груз совершает колебания только под действием упругой силы, возвращающей маятник в положение равновесия.
Если рассмотрим колебания какого-нибудь тела, подвешенного на нерастяжимой нити (рис.3), то сила, вызывающая колебания, не является упругой (по своей природе). В данном случае колебания происходят под действием одной из составляющих силы тяжести Р2 , которая возвращает маятник к положению равновесия. Силы, не упругие по своей природе, но аналогичные им по виду зависимости от смещения, называются квазиупругими (подобными упругим). Примером гармонических колебаний под действием квазиупругих сил могут служить колебания математического и физического маятника.
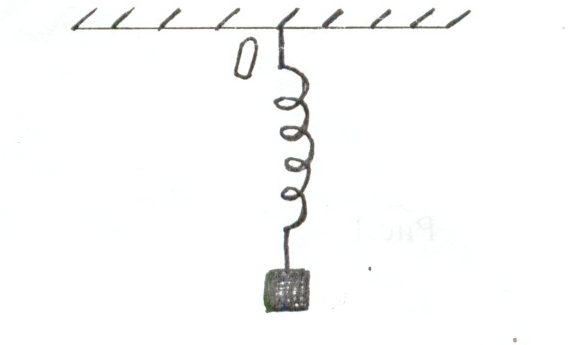(Рис.2)