17. Ньютоновские методы минимализации функции

Метод Ньютона-это методы второго порядка.

X_k+1= x_k-{ɸ’’(x_k)}^-1

Метод Ньютона , имеет очень узкую область сходимости, если их оптим. лежит ближе к Х₀.

Недостатки метода Ньютона, частично устр. В модиф. Методе Ньютона.

X_k+1=x_k-λ_к{ɸ’’(x_k)}^-1ɸ’(x_k) λ_к{ɸ’’(x_k)}^-1 -это обратная матрица Гессе

λ_k=min{ɸ(x_k-λ_k(ɸ’’(х_к))^-1ɸ’(x_k)}

В обратной матрице 2-ая производная не должна равняться -0.

Квази-Ньютоновские методы.

X_k+1 = x_k-λ_кƞ_кφ'(x_k)

18. Квазиньютоновские методы минимизации функции.

По конспекту:

- матрица, которая расч без использования второй производной

!Все что далее, не глядя взято из интернетов, что не совсем похоже на конспект (как минимум по обозначениям), поэтому что писать – выбор ваш!

Квазиньютоновский метод

Описание алгоритма:

Данный метод обладает положительными чертами метода Ньютона, однако, использует информацию только о первых производных. В этом методе приближение к очередной точке в пространстве оптимизируемых параметров задается формулой:

Направление поиска определяется выражением:

,

где - матрица порядка (метрика).

Матрица - вычисляется по формуле.

,

где:

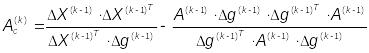(1)

Где изменение градиента на предыдущем шаге.

Данный алгоритм отличается устойчивостью, так как обеспечивает убывание целевой функции от итерации к итерации.

Алгоритм метода:

Шаг 1. Задать: начальную точку х(0). Перейти к шагу 2.

Шаг 2. Вычислить направление поиска s(k). Перейти к шагу 3.

Шаг 3. Произвести поиск вдоль прямой . Перейти

к шагу 4.

Шаг 4. Проверка условия окончания поиска.

Да: закончить поиск;

Нет: перейти к шагу2.

19. Регулярные методы минимизации функций (прямые методы и методы сопряженных направлений). Конспект:

Прямые методы (при работе не используются производные от целевой функции)

Методы сопряженных направлений (тоже не используются производные от целевой функции)

К прямым относят симплексные методы (Нелдера-Мида)

< = что это за рисунок и какому методу – без понятия.

Википедия:

Метод Нелдера —Мида, также известный как метод деформируемого многогранника и симплекс-метод, — метод безусловной оптимизации функции от нескольких переменных, не использующий производной(точнее — градиентов) функции, а поэтому легко применим к негладким и/или зашумлённым функциям.

Суть метода заключается в последовательном перемещении и деформировании симплекса вокруг точки экстремума.

Метод находит локальный экстремум и может «застрять» в одном из них. Если всё же требуется найти глобальный экстремум, можно пробовать выбирать другой начальный симплекс. Более развитый подход к исключению локальных экстремумов предлагается в алгоритмах, основанных на методе Монте-Карло, а также в эволюционных алгоритмах.

Липа какая-то:

Метод сопряженных направлений Пауэлла

Описание алгоритма:

Метод ориентирован на решение задач с квадратичными целевыми функциями. Основная идея алгоритма заключается в том, что если квадратичная функция:

приводится к виду сумма полных квадратов

то процедура нахождения оптимального решения сводится к одномерным поискам по преобразованным координатным направлениям.

В методе Пауэлла поиск реализуется в виде:

вдоль направлений , , называемых -сопряженными при линейной независимости этих направлений.

Сопряженные направления определяются алгоритмически. Для нахождения экстремума квадратичной функции переменных необходимо выполнить одномерных поисков. Алгоритм метода:

Шаг 1. Задать исходные точки , и направление . В частности, направление может совпадать с направлением координатной оси;

Шаг 2. Произвести одномерный поиск из точки в направлении получить точку , являющуюся точкой экстремума на заданном направлении;

Шаг 3. Произв. одномерный поиск из точки в направлении получить точку ;

Шаг 4. Вычислить направление ;

Шаг 5. Провести одномерный поиск из точки (либо ) в направлении с выводом в точку .