8. Этапы формирования математических моделей. Модели структурного уровня.
Структурные модели применяются на ранних этапах проектирования, когда моделью объекта служит ориентированный граф.(орт. граф).
Такой орт. граф включает в себя элементы входящие в объект и рёбра их соединяющие.
Орт. графы структурной модели соответствуют матрице смежности.
Матрица смежности:
V1 |
V2 |
V3 |
V4 |
V5 |
|
|
1 |
|
1 |
1 |
V1 |
|
|
1 |
1 |
|
V2 |
|
1 |
|
1 |
|
V3 |
|
|
1 |
|
1 |
V4 |
1 |
|
|
|
|
V5 |
|
|
|
|
|
|
Строки и столбцы матрицы соответствуют структурам.
Каждый элемент матрицы Сij равен числу рёбер направленных от вершин Vi к вершине Vj.
Отношение между элементами 2-х множеств (вершинами и рёбрами) описывается в виде матрицы инцидентности:
|
Е1 |
Е2 |
Е3 |
Е4 |
Е5 |
Е6 |
Е7 |
Е8 |
Е9 |
Е10 |
V1 |
1 |
-1 |
1 |
1 |
|
|
|
|
|
|
V2 |
|
|
-1 |
|
|
1 |
1 |
-1 |
|
|
V3 |
|
|
|
|
|
|
-1 |
1 |
1 |
-1 |
V4 |
|
|
|
-1 |
1 |
-1 |
|
|
-1 |
1 |
V5 |
-1 |
1 |
|
|
-1 |
|
|
|
|
|
Строки этой матрицы соответствуют вершинам орт. графа, а столбцы рёбрам. Элемент aij=1 если вершина Vi начало для ребра Ej и элемент aij= -1 если вершина Vi конец для ребра Ej
9. Этапы формирования мат моделей. Модели логического уровня
Каждому множеству соответствуют наборы логических отношений. Они отражают причинно-следственные связи и изменение состояния объекта.
Логическая схема устройства
А={a1…a5} подмножество элементов
Дуальный орграф
S={S1….S8} подмножество сигналов
|
S1 |
S2 |
S3 |
S4 |
S5 |
S6 |
S7 |
S8 |
a1 |
|
1 |
1 |
|
-1 |
|
|
|
a2 |
|
1 |
1 |
|
|
-1 |
|
1 |
a3 |
|
|
|
1 |
|
-1 |
|
1 |
a4 |
|
|
|
|
1 |
|
-1 |
|
a5 |
|
|
|
|
|
1 |
|
-1 |
В=[А*S]
Bij=-1, если Sj – выходит из элемента аi
Bij=+1, если Sj – входит в элемент аi
F,G,P – множество логических функций
Хn-множество входных переменных
Yn-множество внутренних переменных
Y’n- множество внутренних переменных, активирующих элементы
Y’(n-1) – множество внутренних переменных относящихся к предыдущему моменту времени.
Логическая модель статического вида (элементы множества переменных безинерционны) но чаще используется динамические модели
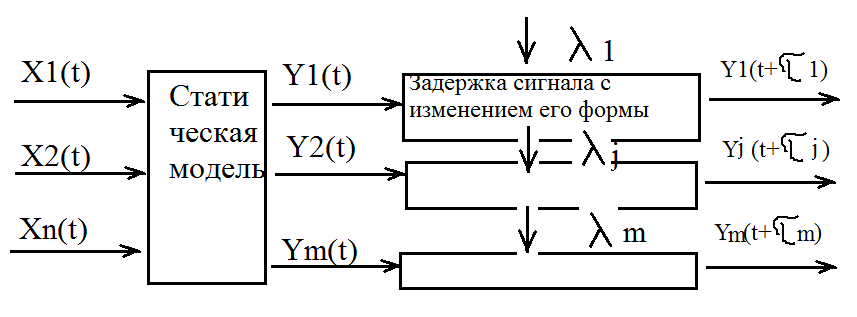
X1(t)…Xn(t) – входные переменные
Y1(t)…Ym(t) – внутренние переменные, активирующие элементы
λ – внешние факторы
τ – временные задержки срабатывания элементов.