Основы метода конечных элементов. Типы элементов и степени свободы.
Метод конечных элементов (MKЭ) представляет собой эффективный численный метод решения инженерных и физических задач. Он широко применяется при проектировании судов, летательных аппаратов, несущих систем многоэтажных зданий и т.п. Для МКЭ характерна ясная физическая трактовка. Его можно рассматривать, в частности, как обобщение классического метода строительной механики - метода перемещений. С другой стороны МКЭ является своеобразной формой часто применяемого вариационного метода Ритца. Различие между традиционной формой метода Ритца и МКЭ состоит в выборе системы координатных функций. Если в методе Ритца функции (обычно ряды) задаются для всей области, то в МКЭ они задаются для ее частей и через множество этих функций определяется состояние системы. Метод конечных элементов предполагает иной подход. Рассматривается элемент конечных размеров, за счет чего осуществляется переход от сплошной системы с бесконечным числом степеней свободы, к системе с конечным числом степеней свободы.
При решении задач методом конечных элементов используются элементы различных типов. Наиболее распространенные типы элементов приведены в табл.. Ниже будут рассматриваться в основном трехузловые треугольные КЭ, как наиболее простые и чаще других применяемые для решения плоской задачи.
Название элемента |
Форма элемента |
|
Число степеней свободы |
стержень |
|
|
2 |
балка |
|
|
6 |
плоский треугольник |
|
|
6 |
треугольник с 6 узлами |
|
|
12 |
плоский четырехугольник |
|
|
8 |
треугольная пластина |
|
|
9 |
Прямоугольная пластина |
|
|
12 |
тетраэдр |
|
|
12 |
треугольник в полярных координатах |
|
|
6 |
24. Примеры использования методов конечных элементов (плоская пластина).
Пример: Пластина
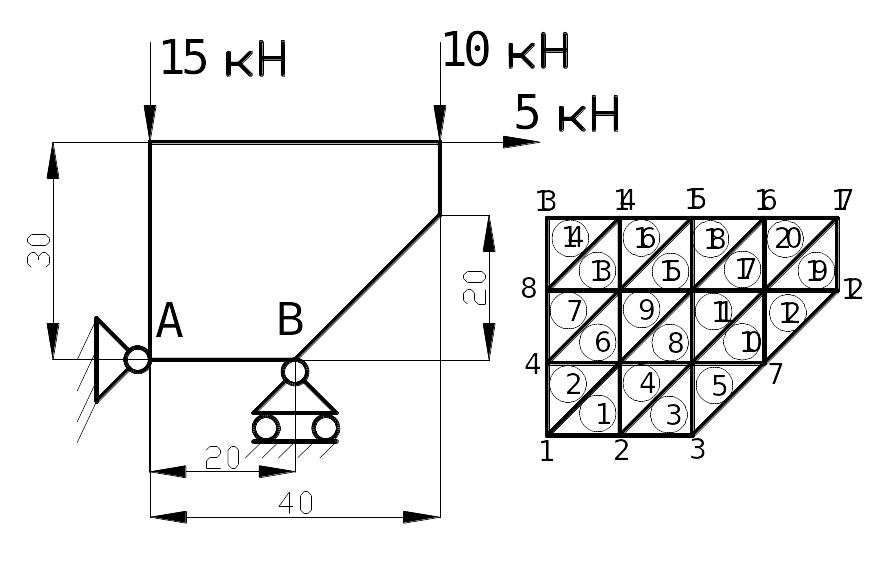
δ=30 мм; Коэффициент Пуассона 0,3; Модуль Юнга 207 МПа
1: М2; 0; 0; 20; 0
2: M3; 0; 10; 30;10
3: M4; 0; 20; 40; 20
4: M4; 0; 30; 40; 30
5: L13; 0; -15000
6: L17; 5400; -10000
7: R1; 0; 0
8: R3;1;0
9: P 0,3
10: E 207000
11: T 30
При расчёте формируется матрица жёсткости, рассчитываются напряжения и деформация.
1. Перемещение узлов
№ point |
X |
Y |
1 |
4,99E-27 |
2,5E-27 |
….. |
…. |
….. |
17 |
1,923E-02 |
-0,0235 |
2.Нагрузки на элементы
EL № |
Sigma X-X |
Sigma Y-Y |
TAV |
1 |
17,1739 |
4,911 |
13,341 |
2 |
1,499 |
3,325 |
16,152 |
….. |
|
|
|
20 |
39,663 |
3,925 |
27,9 |
3. Реакции узлов
№ point |
X |
Y |
1 |
-4,99Е+8 |
-2,49Е+8 |
3 |
0 |
2,74Е+9 |
*************************************************************************
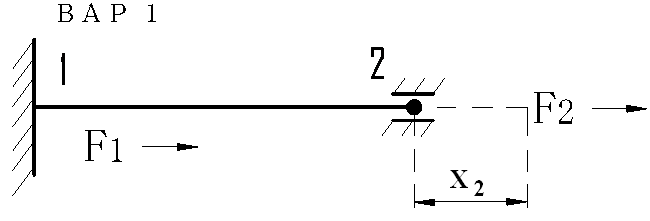
Х1=0; F2=k*x2; F1+F2=0; F1=-F2.
Q1=k*x1; x2 =0; Q2=0; Q1+Q2=0; Q2=-Q1
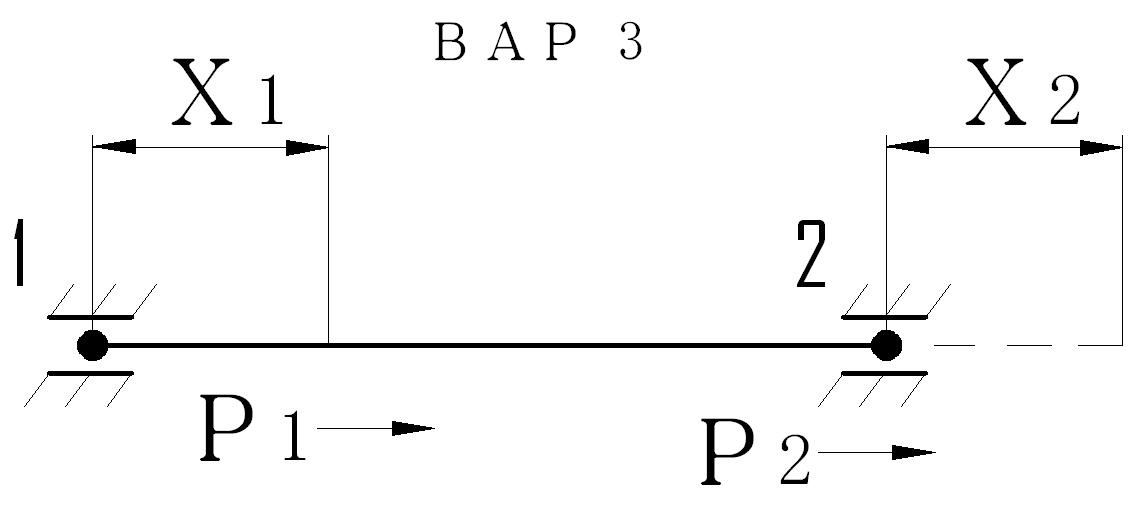
Р1=F1+Q1=-F2+Q1=k*x1-k*x2;
P2=-k*x1+k*x2.
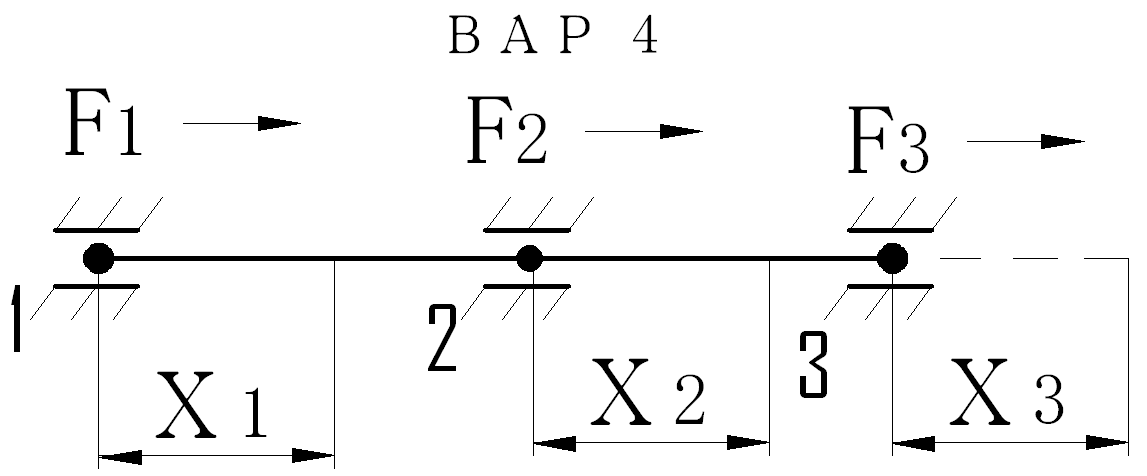
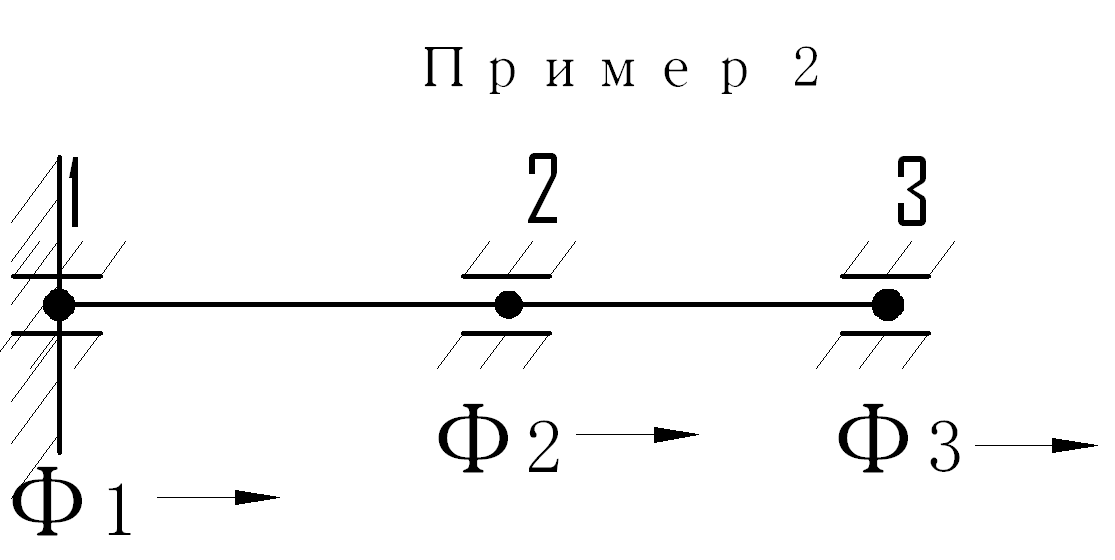
Исходные данные : К=12 кН/м; Ф2= 3 кН; Ф3= 6 кН;
Найти: Ф1; Х2; Х3.
Решение:
Преобразуем
3=24*х2-12*х3
6=-12*х2+12*х3
9=12*х2
х2=0,75 мм
3=24*0,75-12*х3
Х3=1,25 мм
Ф1=-12*0,75=-9кН