26. Графическое изображение вариационного ряда

Гистограмма частот: Полигон частот:

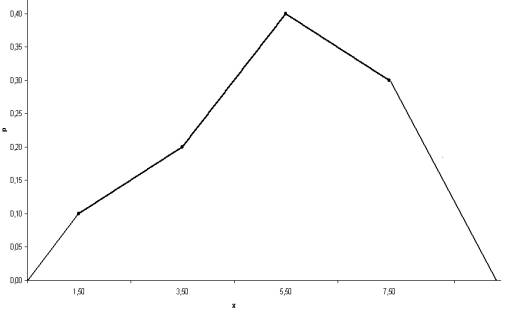
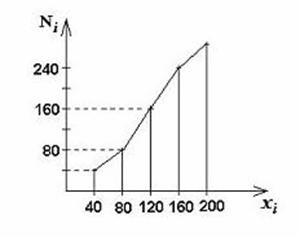
Кумулята и огива(пересекает по диагонали):

27. Мода - значение во множестве наблюдений, которое встречается наиболее часто. Иногда в совокупности встречается более чем одна мода (например: 2, 6, 6, 6, 8, 9, 9, 9, 10; мода = 6 и 9). В этом случае можно сказать, что совокупность мультимодальна. Из структурных средних величин только мода обладает таким уникальным свойством. Как правило мультимодальность указывает на то, что набор данных не подчиняется нормальному распределению.

Медиана - возможное значение признака, которое делит ранжированную совокупность (вариационный ряд выборки) на две равные части: 50 % «нижних» единиц ряда данных будут иметь значение признака не больше, чем медиана, а «верхние» 50 % — значения признака не меньше, чем медиана.

28. Квантиль – это значение, делящее вариационный ряд (ряд сгруппированных частот) на 2 части с опред. пропорциями в каждом их них.

29. Aсимметрия - или коэффициент асимметрии является мерой несимметричности распределения. Например, если асимметрия (показывающая отклонение распределения от симметричного) существенно отличается от 0, то распределение несимметрично, в то время как нормальное распределение абсолютно симметрично. Итак, у симметричного распределения асимметрия равна 0. Асимметрия распределения с длинным правым хвостом положительна. Если распределение имеет длинный левый хвост, то его асимметрия отрицательна.

Эксцесс - или точнее, коэффициент эксцесса измеряет "пикообразность" распределения. Если эксцесс (показывающий "остроту пика" распределения) существенно отличен от 0, то распределение имеет или более закругленный пик, чем нормальное, или, напротив, имеет более острый пик (возможно, имеется несколько пиков). Обычно, если эксцесс положителен, то пик заострен, если отрицательный, то пик закруглен. Эксцесс нормального распределения равен 0.

31. Вариация - это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. Например, работники фирмы различаются по доходам, затратам времени на работу, росту, весу, любимому занятию в свободное время и т.д.

34. Стат.связь – связь, проявляющаяся в кажд.отдельном случае, а в массе случаев в средних величинах в форме тенденций. Частный случай стат.связи – корреляц.связь, при которой некотор.изменению 1 кол.признака, соответствует опред.изменение средн.величины др.признака.

Связь 2 признаков наз-т парной корел-й

Множественн корреляц – нескольк факторов.

Пример кор связей: зависимость объемов продаж от затрат на рекламу.

36. Линейный коэффициент корреляции Пирсона

Пусть X,Y — две случайные величины, определённые на одном вероятностном пространстве. Тогда их коэффициент корреляции задаётся формулой:

где cov — ковариация, D — дисперсия.

37. Корреляция порядковых величин

Коэффициент ранговой корреляции Спирмена

Каждому показателю X и Y присваивается ранг. На основе полученных рангов рассчитываются их разности d и вычисляется коэффициент корреляции Спирмена:

Коэффициент корреляции знаков Фехнера

Подсчитывается количество совпадений и несовпадений знаков отклонений значений показателей от их среднего значения.

C — число пар, у которых знаки отклонений значений от их средних совпадают.

H — число пар, у которых знаки отклонений значений от их средних не совпадают.

Коэффициент ранговой корреляции Кендалла

Применяется для выявления взаимосвязи между количественными или качественными показателями, если их можно ранжировать. Значения показателя X выставляют в порядке возрастания и присваивают им ранги. Ранжируют значения показателя Y и рассчитывают коэффициент корреляции Кендалла:

где S = P − Q.

P — суммарное число наблюдений, следующих за текущими наблюдениями с большим значением рангов Y.

Q — суммарное число наблюдений, следующих за текущими наблюдениями с меньшим значением рангов Y. (равные ранги не учитываются!)