3. Расчёт фильтра

Далее производим расчёт фильтра.

Наиболее широко используют Г-образный индуктивно-емкостной фильтр (рис.3.1).

Рис. 3.1. Схема Г-образного фильтра.

Для сглаживания пульсаций таким фильтром необходимо, чтобы емкостное сопротивление конденсатора для низшей частоты пульсации было много меньше сопротивления нагрузки X_c« R_н, а также много меньше индуктивного сопротивления дросселя для первой гармоники X_c« X_L.

Исходные данные:

постоянное входное напряжение U₀= 14,08(В);

ток нагрузки I₀=0,044 (А);

I_{0 min}=0,008 (А)

амплитуда пульсаций на выходе U_1mвых=0,01 (В);

выпрямитель собран по мостовой схеме (m=2);

амплитуда пульсаций на входе U_1mвх=0,037(В);

Частота пульсации f_c= 50(Гц);

k_пвх=0,037

α_max=5% и α_min=10%.

3.1. Определяем коэффициент сглаживания фильтра:

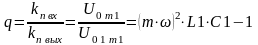(3.1)

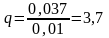
3.2. Необходимое произведение индуктивности и ёмкости равно:

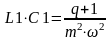(3.2)

Выразив L1 в Генри, а С1 в микрофарадах, получим следующую расчётную формулу:

, (3.3)

где a=f_c/ 50.

3.3. Исходя из условия отсутствия резонанса

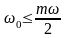, (3.4)

где — собственная частота фильтра;

определяем L_кр, при которой обеспечивается индуктивная реакция фильтра:

(3.5)

Из приложения П3 [2] по I₀=0,044 и L_кр=2,05Гн выбираем стандартный дроссель Д267 L1=2,4 Гн.

3.4. Определяем С1:

(3.6)

Выбираем электролитический конденсатор К50-20 номиналом 5мкФ×50В.

3.5. Уточняем значение коэффициента сглаживания фильтра по (3.1):

, (3.7)

где значения L1 C1 – в системе СИ

4. Расчёт трансформатора

Д

Тр.

алее производим расчёт трансформатора.

U₁₁

U₂₁

Рис. 4.1. Схема трансформатора.

Исходные данные:

максимальное напряжение первичной обмотки U₁₁= 231(В);

максимальное напряжение вторичной обмотки U₂₁= 15,78(В);

максимальный ток вторичной обмотки I₂₁= 0,065 (А);

частота питающей сети f=50 (Гц);

максимальное значение температуры окр. среды Т_с=50⁰С;

максимальный перегрев обмоток ∆Т=50⁰С;

Максимальная активная мощность в нагрузке P=1,03 (Вт)

4.1. Определяем максимальное значение габаритной мощности вторичной обмотки:

(4.1)

4.2. Определяем значение η≈0,65 по кривой 50 Гц (рис.4.1).

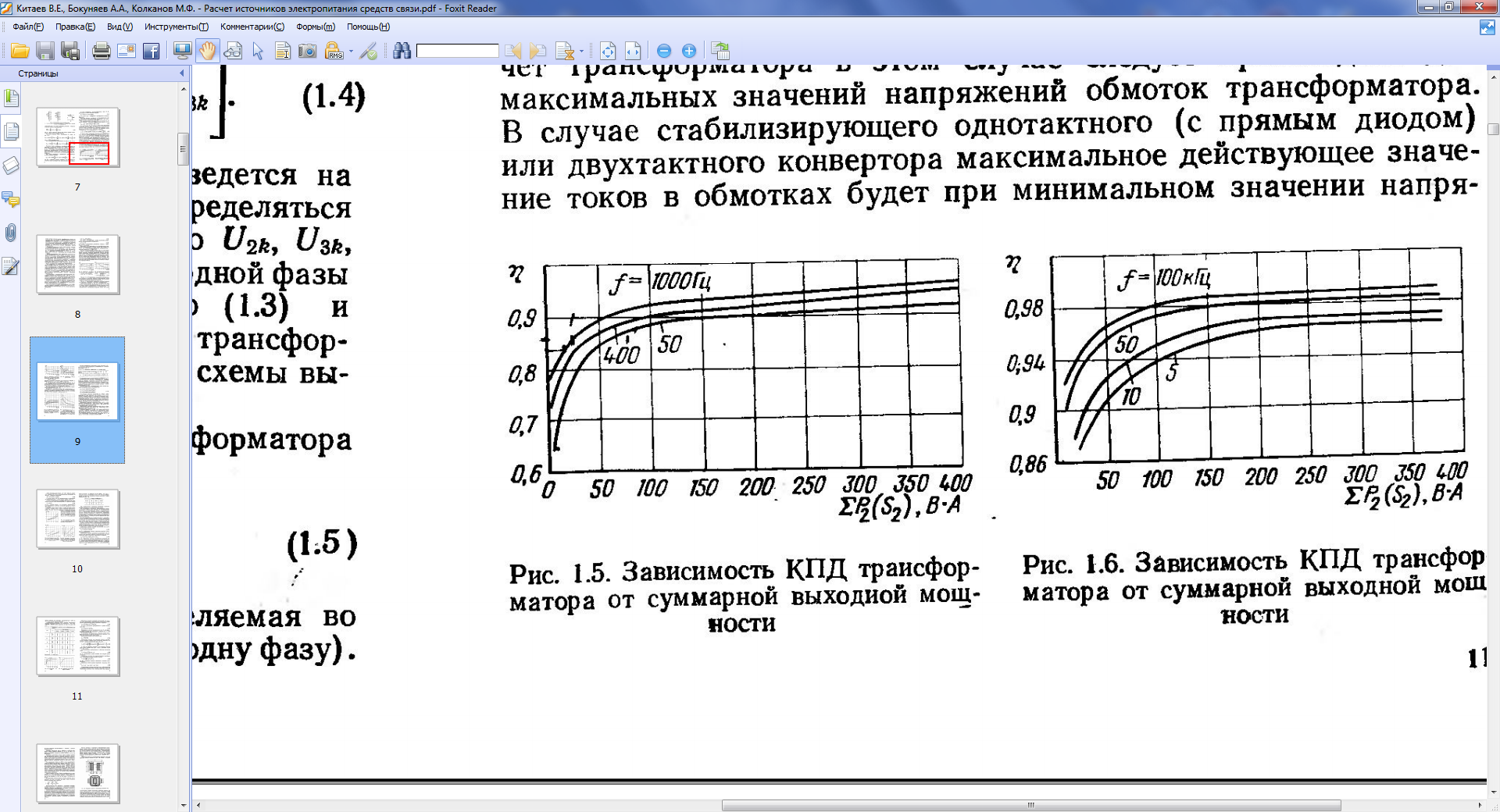
Рис. 4.1. Зависимость КПД трансформатора от суммарной выходной мощности.

Определяем расчётную мощность трансформатора:

(4.2)

4.3. Выбираем конфигурацию и марку материала магнитопровода.

Отдавая предпочтение как наиболее простым по конструкции и наиболее технологичным, выбираем ленточный броневой магнитопровод из стали 3412 толщиной 0,15 мм.

4.4. По кривым (рис.4.2, 4.3, 4.4) находим B, j, K₀

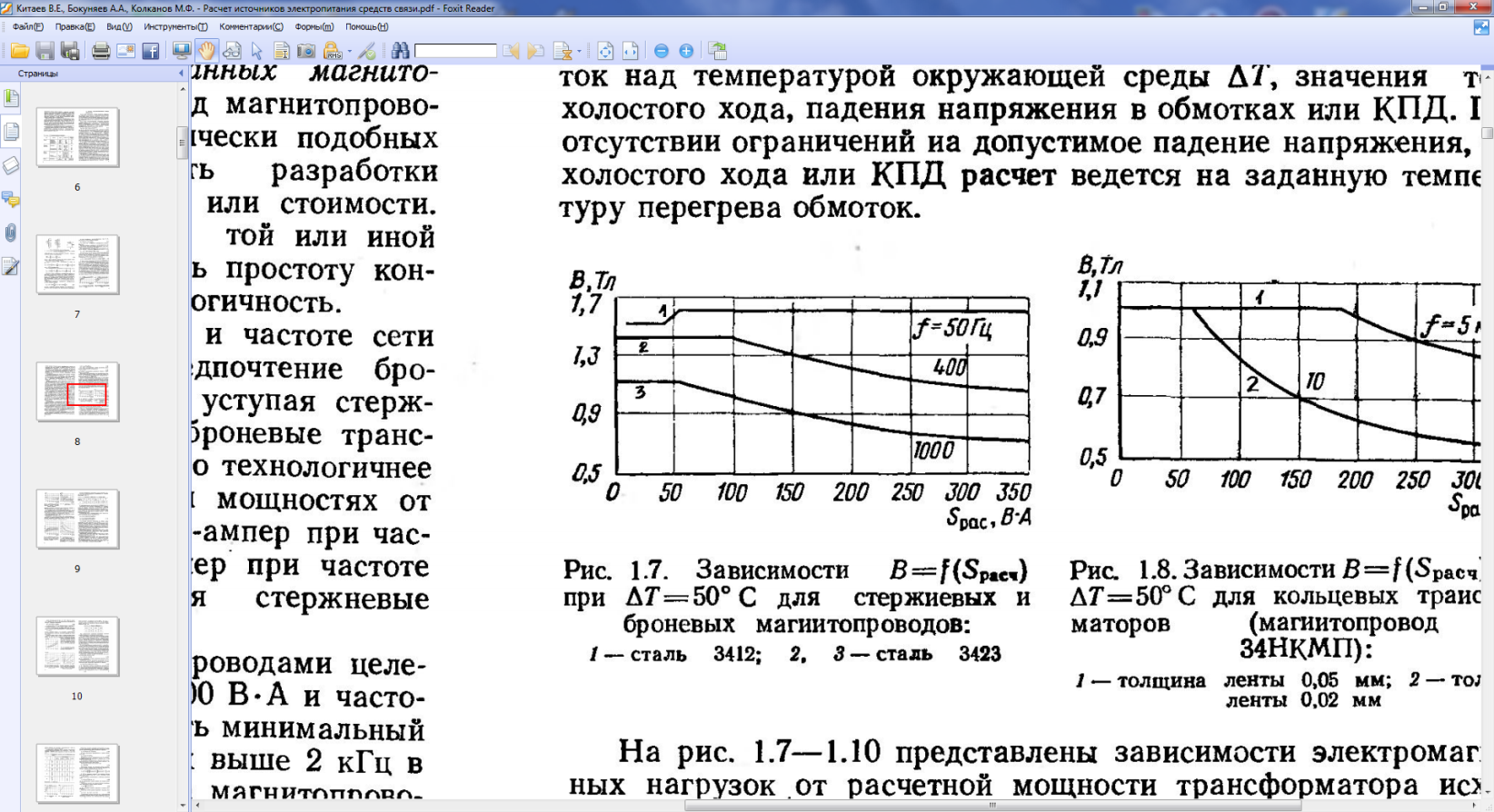
Рис. 4.2. Зависимости B=f(Sрасч) при ∆Т=500С для стержневых и броневых магнитопроводов: 1- сталь 3412; 2,3 – сталь 3423.

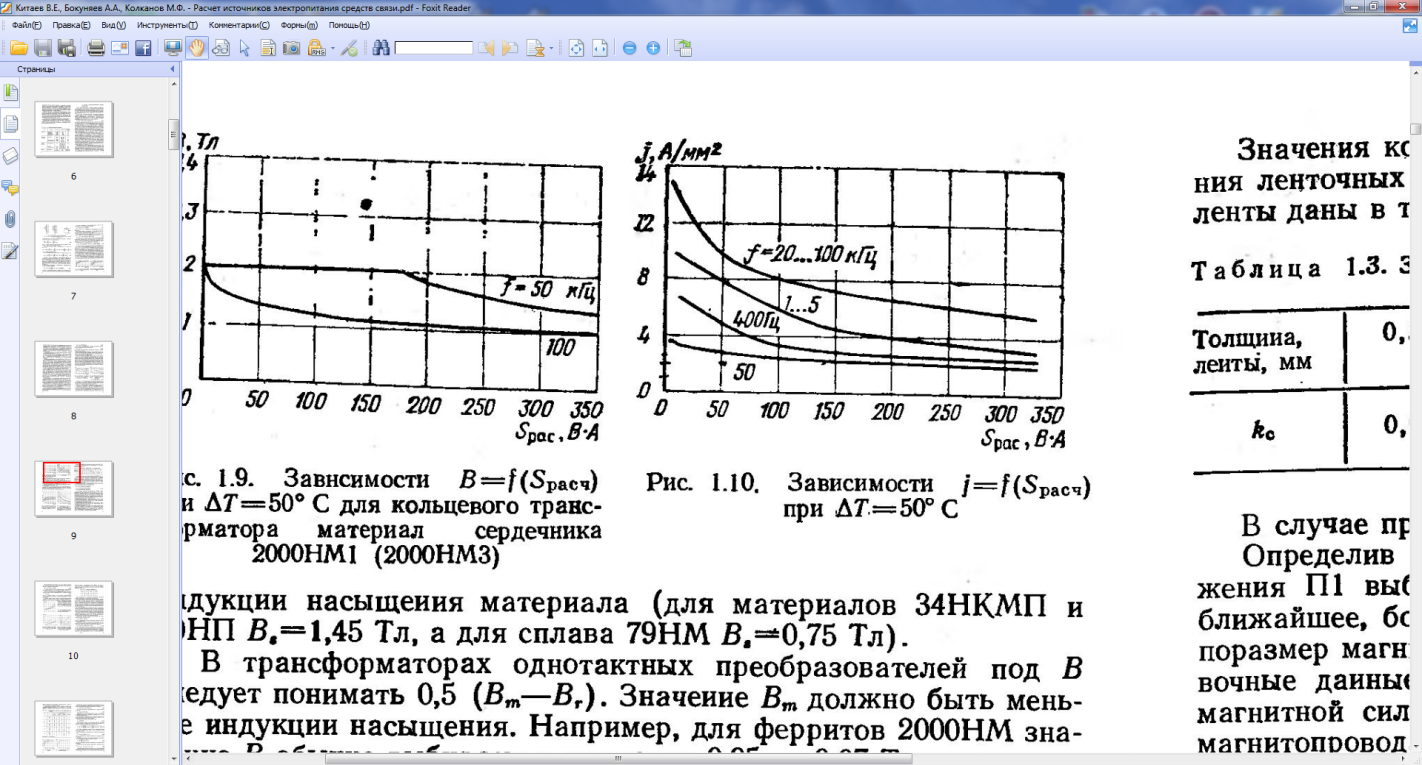
Рис. 4.3. Зависимости j= f(Sрасч) при ∆Т=500С

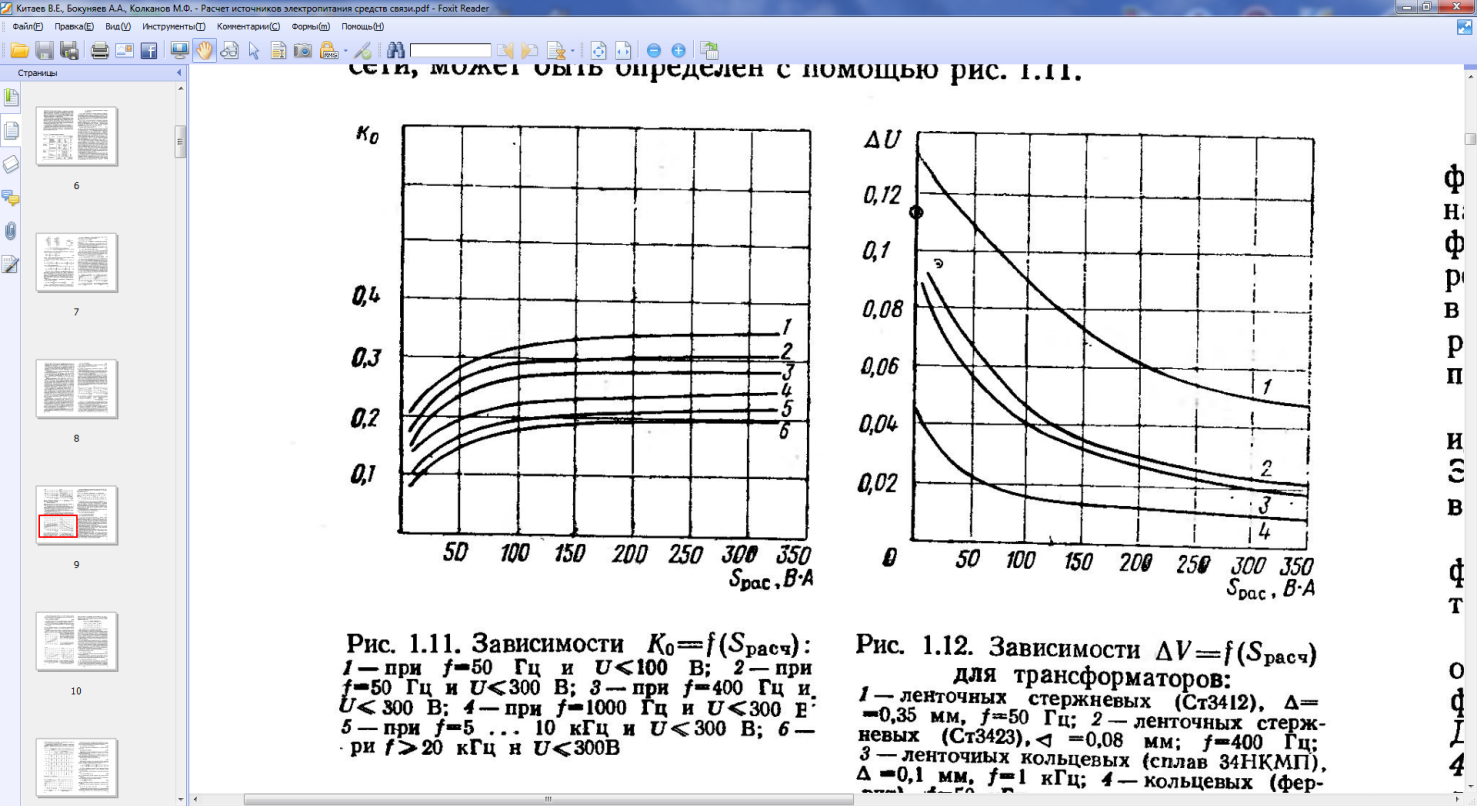
Рис. 4.4. Зависимости K0= f(Sрасч): 1- при f=50Гц и U≤100В; 2- при f=50Гц и U≤300В.

B=1,5 (Тл); j=3,8 (А/мм²); K₀=0,2

По таблице 4.1 находим значение k_с=0,9.

Таблица 4.1.

Зависимость коэффициента k_с от толщины ленты

Толщина ленты, мм	0,5	0,35	0,15	0,1…0,08	0,05	0,02
kс	0,96	0,93	0,9	0,85	0,75…0,8	0,65…0,7

Для выбора типоразмера магнитопровода необходимо рассчитать произведение:

(4.3)

При k_ф=1,11 вычисляем:

4.5. Выбираем по приложению П1.1 [2] ленточный магнитопровод типа ШЛ 10×10 (рис.4.5) с параметрами (табл.4.2).

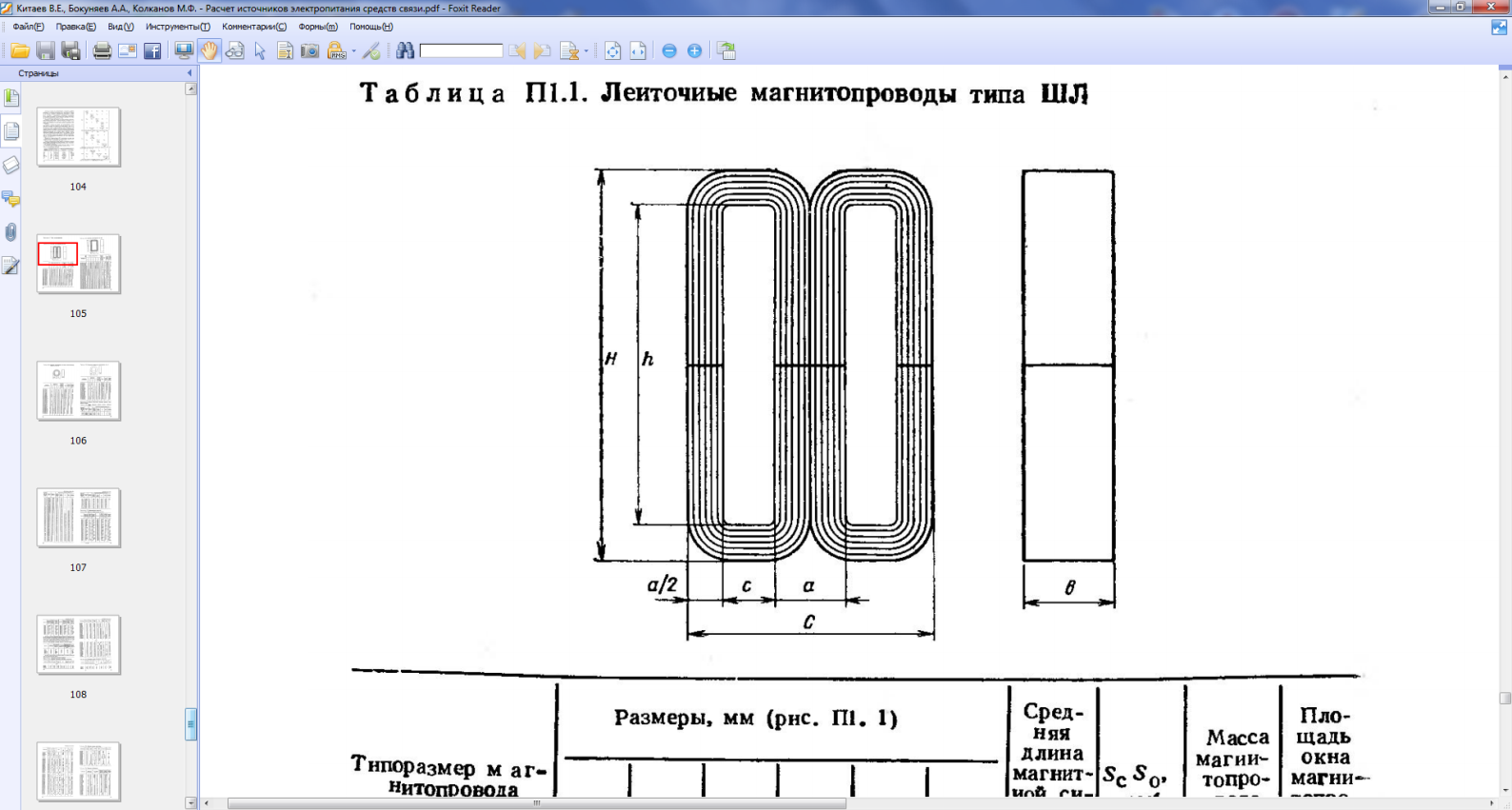
Рис. 4.5. Ленточныймагнитопровод типа ШЛ.

Таблица 4.2.

Параметры ленточногомагнитопровода ШЛ 16×16

Размеры, мм						Ср.длина магнит-ной силовой линии lc, см	Sc·S0 см4	Масса магнито-провода Gст, кг	Площадь окна магнито-провода S0, см2
a	b	h	c	C	H
10	10	25	10	40	35	8,5	2,5	0,057	2,5

6. Определяем по зависимости (рис.4.6) падение напряжения в обмотках трансформатора ∆U. ∆U=0,13.

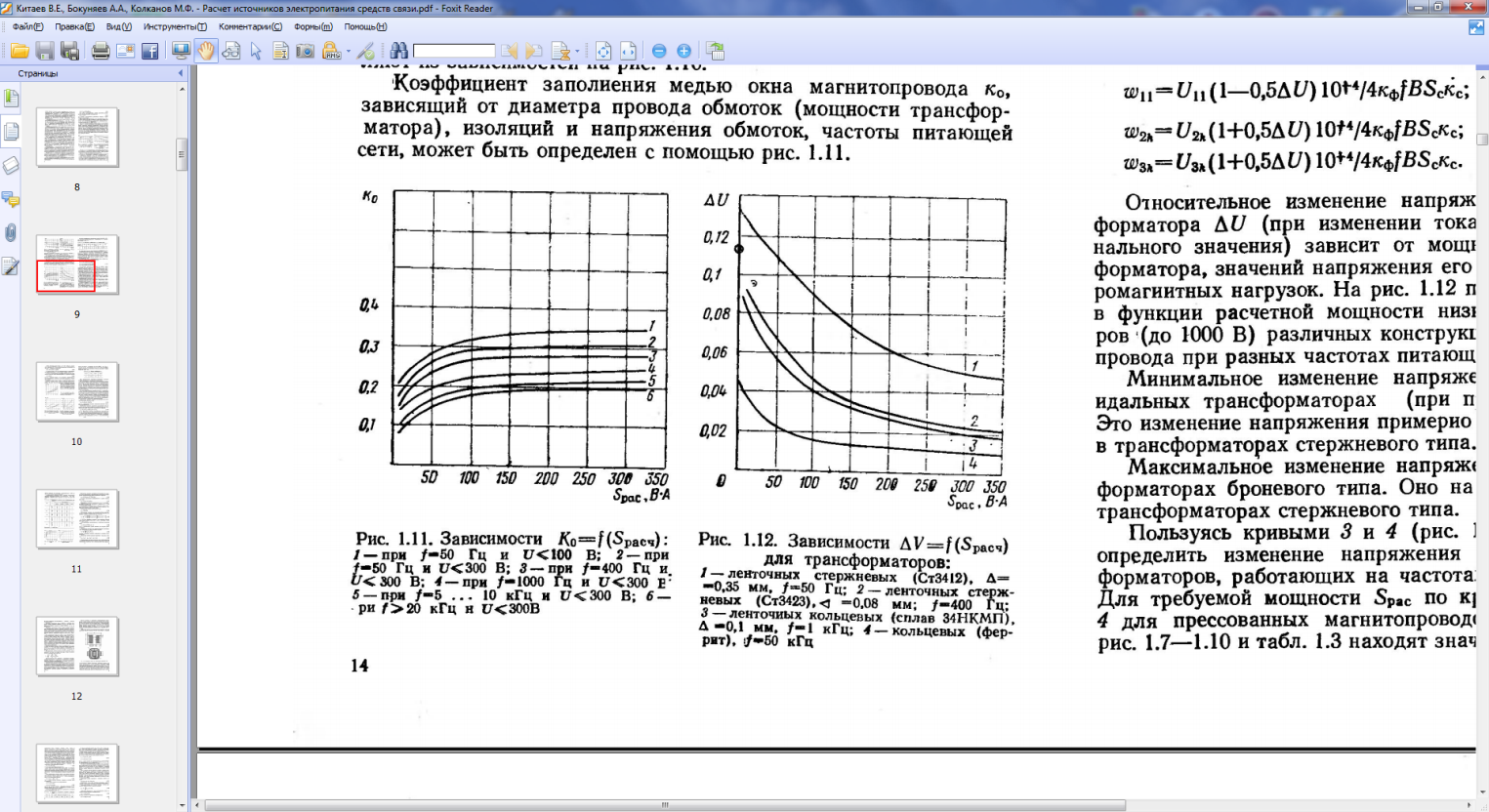
Рис. 4.6. Зависимости ∆U=f(S_расч) для трансформаторов:

1-ленточных стержневых (ст3412), ∆=0,35 мм, f=50Гц.

Находим число витков первичной ω₁₁ и вторичной ω₂₁ обмоток:

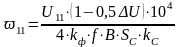(4.4)

S_c=a×bS_c=1,0×1,0=1(см²)

(4.5)

4.7. Определяем удельные потери в магнитопроводеP_уд=1,5 (Вт/кг) по рис. 4.7.

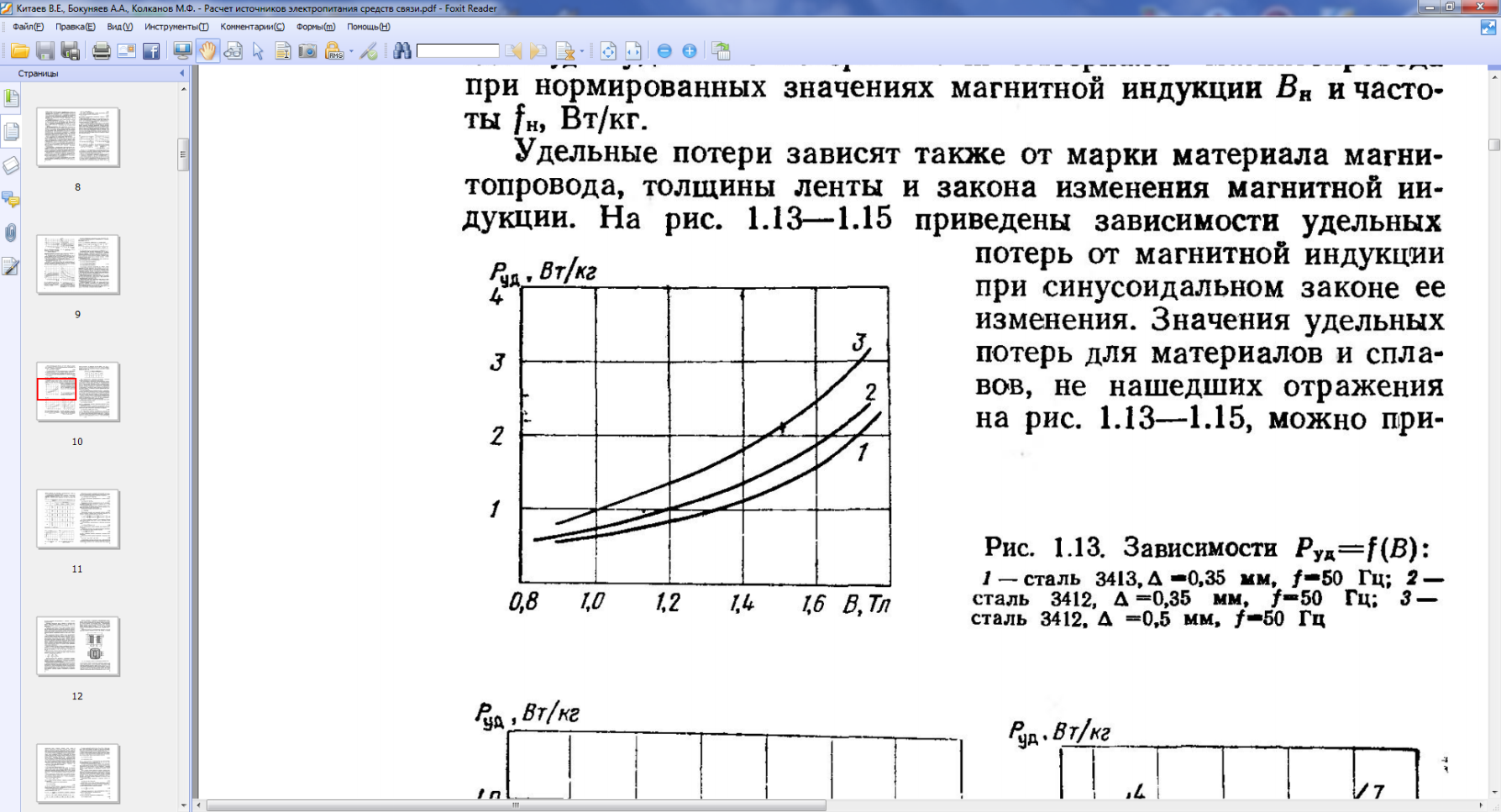
Рис. 4.7. Зависимости P_уд=f(B):

2-(ст3412), ∆=0,35 мм, f=50Гц; 3-(ст3412), ∆=0,5 мм, f=50Гц.

Потери в магнитопроводе исходя из массы магнитопровода и удельных потерь:

P_СТ= P_УД · G_СТ (4.6)

где G_СТ — масса магнитопровода (табл.4.2)

P_СТ= 1,5· 0,057=0,0855 (Вт)

4.8. Действующее значение активной составляющей тока холостого хода I_0a

, (4.7)

где U₁₁ — действующее значение напряжения первичной обмотки трансформатора, В.

Вычисляем действующее значение реактивной составляющей тока холостого хода, исходя из значения напряжённости поля H=80 (А/м) (рис. 4.8):

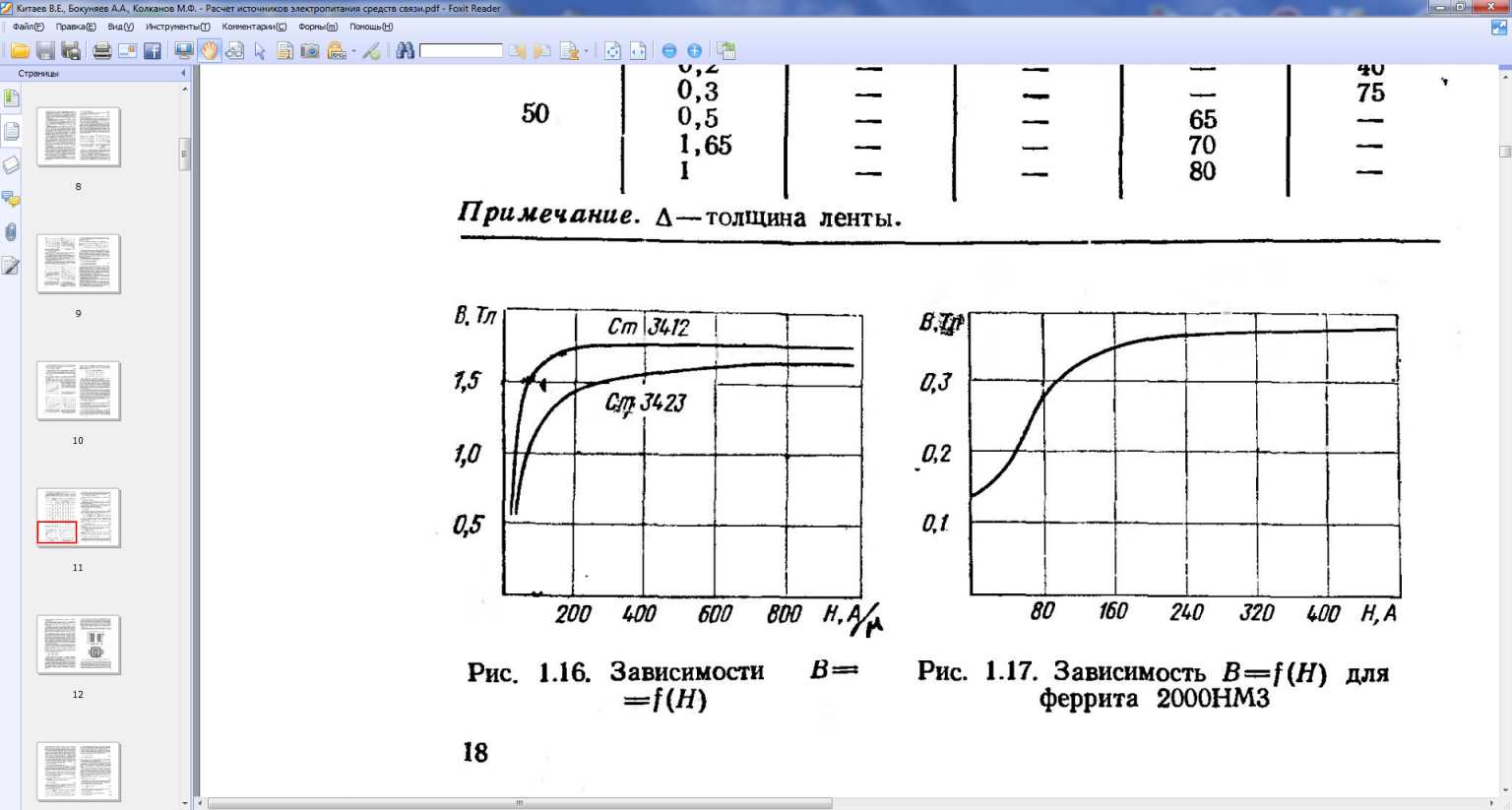
Рис. 4.8. Зависимости B=f(H).

, (4.8)

где H — эффективное значение напряжённости магнитного поля, А/м, соответствующее максимальной магнитной индукции B;

l_c — средняя длина магнитной силовой линии (табл.6), см;

n_з — число немагнитных зазоров (для броневого трансформатора n_з =2);

l_з — длина немагнитного зазора (для ленточных трансформаторов l_з =0,002 см;

ω₁₁— число витков первичной обмотки.

Действующее значение тока холостого хода

(4.9)

4.9. Действующее значение тока первичной обмотки:

(4.10)

4.10. Определяем поперечное сечение проводов обмоток исходя из j=3,8 (А/мм²)

; (4.11)

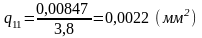
Выбираем по приложению П2 [2] для всех обмоток провод марки ПЭВ-1.

Для первичной обмотки: стандартный провод q₁₁=0,00503 мм²; d₁₁=0,105 мм; d₁₁’=0,08; g₁₁=0,0447 г.

Для вторичной обмотки: стандартный провод q₂₁=0,01767 мм²; d₁₁=0,18 мм; d₁₁’=0,15; g₂₁=0,157 г.

Действительная плотность тока в обмотках

Средняя плотность тока

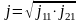
4.11. Конструктивный расчёт трансформатора.

Рис. 4.9. Размещение обмоток на магнитопроводе броневого типа.

Высота одного слоя первичной обмотки броневого трансформатора (рис. 4.9) составляет:

, (4.12)

где h — высота окна магнитопровода (табл.6), мм;

δ_з=0,5…1 мм – зазор между гильзой и магнитопроводом, принимаем 0,5 мм;

δ_щ=1…3 мм – толщина гильзы (каркаса), принимаем 1мм.

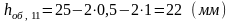
Число витков в одном слое каждой обмотки

, (4.13)

где d₁₁, d₂₁ — диаметр провода с изоляцией первичной и вторичной обмоток, мм;

k_у11, k_у21 — коэффициенты укладки, учитывающие неплотность намотки обмоток (в нашем случае k_у11= k_у21=0,9.

Число слоёв каждой из обмоток

, (4.14)

где p₁, p₂₁ — принимают значения, равные 1 для обмоток без вывода и с выводом нулевой точки;

m₁ — число катушек на магнитопроводе (для броневого трансформатора m₁=1);

ω₁₁, ω₂₁ — число витков обмоток.

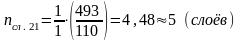
Радиальные размеры обмоток

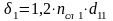
(4.15)

Радиальный размер всех обмоток

(4.16)

где δ₀=0,22…0,3 мм – толщина изоляции обмоток.

Свободный промежуток в окне магнитопровода между катушкой и ярмом

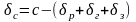(4.17)

Полученное значение больше допустимого предела в 1…1,5 мм.

4.12. Проверочный расчёт трансформатора.

Определяем массу меди обмоток трансформатора:

средний радиус витка первичной обмотки трансформатора

(4.18)

где δ_з =0,5 — толщина зазора;

δ_г =0,25 — толщина гильзы.

средняя длина витка первичной обмотки трансформатора

(4.19)

средний радиус витка вторичной обмотки трансформатора

(4.20)

средняя длина витка вторичной обмотки трансформатора

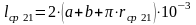(4.21)

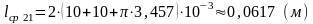
Масса меди первичной обмотки трансформатора

(4.22)

где ω₁ — число витков первичной обмотки;

g₁₁— масса одного метра провода (п.4.10).

Масса меди вторичной обмотки трансформатора

(4.23)

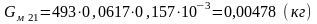
Суммарная масса меди трансформатора

4.13. Расчёт массы изоляции и массы трансформатора.

Коэффициент заполнения окна магнитопровода медью:

(4.24)

где q₁₁ и q₂₁ — площади поперечного сечения проводов;

S₀ — поперечное сечение окна магниопровода (табл.4.2), см².

Масса изоляции:

(4.25)

где γ_ИЗ ≈ 1 г/см³ — удельная масса изоляции;

k_ИЗ = 0,7 — коэффициент укладки изоляции.

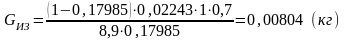
Масса трансформатора:

(4.26)

где G_c —масса магнитопровода (табл. 4.2).

4.14. Расчёт активного сопротивления каждой обмотки и относительные значения активной и реактивной составляющих напряжения короткого замыкания.

Активное сопротивление первичной и вторичной обмоток при максимальной температуре окружающей среды:

(4.27)

где k_t=1+0,04(T_c+∆T-20) — коэффициент, учитывающий увеличение удельного сопротивления меди с поваышением температуры;

T_c— максимальная температура среды, ⁰С;

∆T=50⁰С — температура перегрева обмоток;

k_f— коэффициент увеличения сопротивления провода в зависимости от частоты тока питающей сети (в данном случае k_f=1).

Активное сопротивление вторичной обмотки, приведённое к первичной обмотке:

(4.28)

Относительное значение активной составляющей напряжения короткого замыкания:

(4.29)

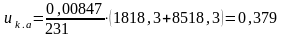
Относительное значение реактивной составляющей напряжения короткого замыкания:

(4.30)

где μ₀=4η·10^-7 Гн/м — магнитная постоянная;

ν=1 — число стержней магнитопровода, несущих обмотки.

Относительное значение напряжения короткого замыкания:

(4.31)

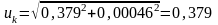
4.15. Определяем потери в обмотках и КПД трансформатора.

Потери в меди обмоток:

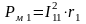
(4.32)

Суммарные потери в меди обоих обмоток:

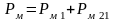
Коэффициент полезного действия трансформатора:

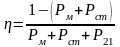(4.33)

4.16. Определяем температуру перегрева и рабочую температуру обмоток.

Общая поверхность охлаждения S_охл= S_{охл к} + S_охлст складывается из поверхности охлаждения катушки и магнитопровода.

(4.34)

(4.35)

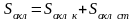
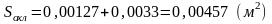
Температура перегрева:

(4.36)

Рабочая температура проводов обмоток:

(4.37)