2 Лабораторная работа эмк-3 к. Изучение поляризации диэлектрика и определение емкости конденсатора
Цель работы: изучение поляризации диэлектрика и определение электрофизических свойств конденсатора.
Задачи:
- градуировка баллистического гальванометра и определение емкости конденсатора в зависимости от его геометрических параметров;
- изучение электрофизических свойств конденсатора при неизменном напряжении на его обкладках;
- изучение электрофизических свойств конденсатора при его неизменном заряде.
2.1 Методика работы
Метод измерения емкости
конденсатора
основан на зарядке конденсатора до
известного значения напряжения
,
измерении его заряда
и
вычислении по формуле
.
(2.1)
Заряд конденсатора измеряется
c помощью зеркального гальванометра,
работающего в баллистическом режиме
(
).
Здесь
-
длительность импульса тока, проходящего
через гальванометр,
-
период собственных колебаний гальванометра.
В таком режиме максимальный отброс
светового
«зайчика» по шкале прибора будет
пропорционален заряду
.
До начала измерений заряда с помощью
баллистического гальванометра
последний нужно проградуировать,
используя конденсатор известной
емкости
,
т.е. снять зависимость
от
.
Емкость плоского конденсатора равна
,
(2.2)
где - электрическая постоянная;
-
диэлектрическая проницаемость среды;
- площадь обкладки;
-
расстояние между обкладками (пластинами)
конденсатора.
Электрическое поле
плоского конденсатора является
однородным
и
при отсутствии диэлектрика (для воздуха
)
характеризуется напряженностью
поля
сторонних зарядов [1]
(2.3)
и электрическим смещением (или электрической индукцией)
,
(2.4)
где - поверхностная плотность сторонних зарядов .
Поле вектора можно изображать с помощью силовых линий, которые начинаются и кончаются лишь на сторонних зарядах. Как видно из (2.4), направления и совпадают.
При заполнении пространства между
обкладками диэлектриком с проницаемостью
свойства
конденсатора изменяются. Под действием
поля диэлектрик поляризуется:
дипольные моменты молекул вещества
ориентируются в направлении поля и
на противоположных сторонах диэлектрика
(см. рис. 2.1) появляются связанные заряды
.
Эти заряды создадут внутри
диэлектрика однородное поле,
напряженность которого равна
.
Вне диэлектрика 
.
Оба поля
и
направлены
навстречу друг другу и, следовательно,
в пространстве между обкладками
конденсатора напряженность результирующего
поля равна
.
(2.5)
Вне диэлектрика
.
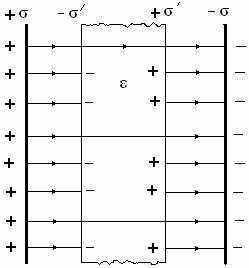
Рисунок 2.1
Так как поверхностная плотность связанных
зарядов
,
то, подставив это значение в формулу
(2.5), получим
,
откуда
,
(2.6)
т.е.
диэлектрическая проницаемость
показывает,
во сколько раз ослабляется поле в
диэлектрике по сравнению с вакуумом,
поэтому густота силовых линий
в
диэлектрике в
раз
меньше, чем в вакууме.
Для понимания явления поляризации диэлектрика и выяснения физического смысла величин и , рассмотрим два примера полей в конденсаторе.
Пример 1. При введении
диэлектрика в зазор напряжение между
обкладками остается неизменным (
,
источник не отключен от конденсатора):
а) пусть диэлектрик полностью
заполняет пространство между обкладками
конденсатора. Вследствие поляризации
диэлектрика емкость конденсатора
увеличивается в
раз,
т.е.
и,
следовательно, увеличиваются заряды
на обкладках конденсатора. Однако
приращение сторонних зарядов
компенсируется
появлением связанных зарядов
,
и поэтому напряженность поля
остается
неизменной
,
(2.7)
где
-
поле сторонних зарядов
;
- электрическое смещение поля.
,
(2.8)
т.е. значение
вектора электрического смещения
увеличивается
в
раз
, т.к. источниками линий
являются
сторонние заряды
;
б) пусть диэлектрик заполняет только вторую половину зазора (рис. 2.2). Емкость конденсатора вследствие поляризации диэлектрика уменьшается и определяется равенством
,
(2.9)
Рисунок 2.2
где
-
емкость воздушной половины зазора;
-
емкость второй половины зазора с
диэлектриком
.
С увеличением за счет источника сторонних
зарядов
на
обкладках и появления связанных
зарядов
на
диэлектрике электрическое поле в
первой (воздушной) половине зазора
характеризуется напряженностью
и
смещением 
,
на второй половине зазора (с диэлектриком)
.
(2.10)
Так как электрическое смещение определяется только сторонними зарядами , то
.
(2.11)
Поскольку здесь
,
то
.
Определяем соотношения между
,
и
или
,
откуда
(2.12)
и
,
(2.13)
т.е. напряженность
поля
увеличивается
по сравнению с
,
а его линии начинается на сторонних
зарядах
первой
обкладки конденсатора и кончаются как
на связанных отрицательных зарядах
диэлектрика,
так и на сторонних зарядах
на
второй обкладке (рисунок 2.2).
Пример 2. Заряд конденсатора
остается неизменным (источник после
зарядки отключается,
):
а) диэлектрик с проницаемостью
полностью
заполняет зазор (рис. 2.1). Под действием
поля он поляризуется и на нем появляются
связанные заряды
,
которые создают поле напряженностью
,
направленное против поля сторонних
зарядов напряженности
,
следовательно, в этом случае напряженность
в зазоре равна
,
(2.14)
т.е. поле ослабляется в раз.
Электрическое смещение , вследствие постоянства сторонних зарядов, остается неизменным и равным смещению в вакууме
;
(2.15)
б) диэлектрик заполняет только вторую половину зазора (рис 2.2). В этом случае на воздушной половине зазора, вследствие постоянства сторонних зарядов напряженность поля равна
.
(2.16)
Линии начинаются на сторонних зарядах на первой обкладке и кончаются как на связанных зарядах , так и на сторонних зарядах второй обкладки .
На второй половине зазора с
диэлектриком
,
вследствие его поляризации и
появления поля
связанных
зарядов
,
напряженность равна
,
(2.17)
т.е. поле в диэлектрике ослаблено в раз. Электрическое смещение так же, как и в первом случае, остается неизменным и равно
.
(2.18)