Активные элементы электрических цепей

Активными называются элементы цепи, которые отдают энергию в цепь, т.е. источники энергии. Существуют независимые и зависимые источники. Независимые источники: источник напряжения и источник тока.

Источник напряжения - идеализированный элемент электрической цепи, напряжение на зажимах которого не зависит от протекающего через него тока.

Внутреннее сопротивление идеального источника напряжения равно нулю.

Источник тока – это идеализированный элемент электрической цепи, ток которого не зависит от напряжения на его зажимах.

Внутреннее сопротивление идеального источника тока равно бесконечности.

Источники напряжения (тока) называются зависимыми (управляемыми), если величина напряжения (тока) источника зависит от напряжения или тока другого участка цепи. Зависимыми источниками моделируются электронные лампы, транзисторы, усилители, работающие в линейном режиме.

Различают четыре типа зависимых источников.

1. ИНУН – источник напряжения, управляемый напряжением: а) нелинейный, б) линейный, μ – коэффициент усиления напряжения

2. ИНУТ - источник напряжения, управляемый током: а) нелинейный, б) линейный, γн – передаточное сопротивление

3. ИТУТ – источник тока, управляемый током: а) нелинейный, б) линейный, β - коэффициент усиления тока

4. ИТУН – источник тока, управляемый напряжением: а) нелинейный, б) линейный, S - крутизна (передаточная проводимость)

Характеристика источников питания:

Е идеальн. Напряжение падает при увеличении нагрузки, I_к – ток короткого замыкания, Е – источник напряжения, ЭДС (внутреннее сопротивление отсутствует) – идеализированный источник питания.  – ток короткого замыкания. P=EI – нагрузка – мощность источника напряжения. P=I²r_в+I²r – полный расход мощности.  – допустимая плотность тока.

6.

№7 схема замещения, электрическая схема, в которой все реальные элементы заменены максимально близкими по функциональности цепями из идеальных элементов.

В схемах замещения используются перечисленные ниже идеальные элементы. Предполагается также, что геометрические размеры эквивалентной схемы настолько малы, что какие-либо эффекты длинных линий отсутствуют, то есть эквивалентная схема рассматривается как система с сосредоточенными параметрами.

Резистор. Идеальный резистор характеризуется только сопротивлением. Индуктивность, емкость, а также сопротивление выводов равны нулю.

Конденсатор. Идеальный конденсатор характеризуется только ёмкостью. Индуктивность, утечка, тангенс угла потерь,диэлектрическое поглощение а также сопротивление выводов равны нулю.

Катушка индуктивности. Идеальная катушка индуктивности характеризуется только индуктивностью. Емкость,сопротивление потерь, а также сопротивление выводов равны нулю.

Источник ЭДС. Идеальный источник ЭДС характеризуется только своим напряжением. Внутреннее сопротивление и сопротивление выводов равны нулю.

Источник тока. Идеальный источник тока характеризуется только своим током. Утечка равна нулю.

Проводники. Элементы эквивалентной схемы соединены идеальными проводниками, то есть индуктивность, емкость и сопротивление проводников равны нулю.

Неоднозначность

Для любой электрической схемы можно составить сколько угодно различных эквивалентных схем — количество их ограничивается только соображениями целесообразности. Для одной схемы имеет смысл составлять несколько эквивалентных схем по следующим причинам:

Учет различных эффектов. Эквивалентная схема составляется тем или иным образом в зависимости от того, какие эффекты мы хотим с ее помощью описать. Например, для нахождения рабочей точки по постоянному току требуется одна эквивалентная схема, а для расчета АЧХ — совершенно другая.

Поэтапное упрощение. В процессе расчета схемы целесообразно заменять ее сложные участки простыми эквивалентными цепями. Например, цепь из последовательно включенных резисторов можно заменить одним резистором с суммарным сопротивлением. В полученной упрощенной схеме можно вновь применить некоторую замену и т.д.

Ограничения

Эквивалентная схема является линейной системой, поэтому нелинейные эффекты реальных схем не могут быть смоделированы путем составления эквивалентных схем.

Частичным выходом из этого затруднения является рассмотрение нелинейной системы в малосигнальном приближении для конкретной рабочей точки, при этом нелинейные эффекты малы и ими можно пренебречь. Данный подход позволяет не описать нелинейные эффекты, а всего лишь ограничиться случаем, когда они пренебрежимо малы.

Эквивалентная схема не может абсолютно точно соответствовать реальной схеме вследствие огромного числа распределенных паразитных эффектов в последней. Однако это и не требуется: эквивалентная схема составляется с достаточной для конкретной задачи детализацией.

№8 Все элементы можно разделить на две группы: 1.     Активные элементы или источники электрической энергии. 2.     Пассивные элементы или потребители электрической энергии. К первой группе относятся источники тока и напряжения. Ко второй группе относятся активные и реактивные потребители. Графические изображения элементов и их основные параметры показаны в таблице.

Элемент	Графическое изображение	Параметр	Ед. измерения	Дополнительные ед. измерения
1	2	3	4	5
Источник ЭДС		ЕДС	Вольт (В)	-
Источник тока		Ток	Ампер (А)	-
Резистивный элемент (резистор)		Сопротивление	Ом (Ом)	1 кОм=103 Ом 1 мОм=106 Ом 1 гОм=109 Ом
Индуктивный элемент (катушка индуктивности)		Индуктивность	Генри (Гн)	1 мГн=10-3 Гн 1 мкГн=10-6 Гн
Емкостной элемент (конденсатор)		Емкость	Фарада (Ф)	1 мкФ=10-6 Ф 1 нФ=10-9 Ф 1 пФ=10-12 Ф

Закон Ома для участка электрической цепи	Сила тока на участке электрической цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению участка		Следствия:   - сопротивление равно отношению напряжения к силе тока;  - напряжение (падение напряжения) равно произведению силы тока и сопротивления
Закон Ома для полной электрической цепи	Сила тока в электрической цепи прямо пропорциональна ЭДС источника и обратно пропорциональна полному сопротивлению цепи (сумме внешнего и внутреннего сопротивлений)		Следствие:   - напряжение на зажимах реального источника отличается от ЭДС на величину падения напряжения на внутреннем сопротивлении источника
Первый закон Кирхгофа	Алгебраическая сумма токов в узле электрической цепи равна нулю (сумма токов, входящих в узел электрической цепи равна сумме токов, выходящих из узла)		Правило составления уравнений: токи, входящие в узел, записываются со знаком «плюс», выходящие из узла - со знаком «минус»
Второй закон Кирхгофа	Алгебраическая сумма ЭДС, действующих в контуре электрической цепи, равна алгебраической сумме падений напряжения на сопротивлениях, входящих в этот контур		Правила составления уравнений: ЭДС записываются со знаком «плюс», если их направление совпадает с направлением обхода контура, со знаком «минус» - если не совпадает; падение напряжения записываются со знаком «плюс», если направление тока совпадает с направлением обхода контура, со знаком «минус» - если не совпадает
Закон Джоуля - Ленца	Количество теплоты, выделяемой в проводнике при прохождении по нему электрического тока прямо пропорционально произведению квадрата силы тока, сопротивлению проводника и времени прохождения тока через проводник

№9

№10

Теория цепей имеет два направления:

• анализ электрических цепей

• синтез (создания новых) электрических цепей.

     При анализе электрической цепи, ее топология (схема), как правило, нам известна. В большинстве случаев известны даже номиналы всех электронных компонентов цепи, но не всегда. И наша задача рассчитать все (или часть) токов и напряжений. Если неизвестны параметры каких-то компонентов цепи, то их нужно рассчитать. Со всеми этими задачами справиться можно, если хорошо владеть методиками расчета электрических цепей.

 

Рис.1 Пример электрической цепи, которую нужно проанализировать

     Синтез электрических цепей задача более сложная и неоднозначная. При создания новой цепи мы еще не знаем с каких элементов она будет состоять, какие у них номиналы и как эти элементы будут соеденены между собой (мы не знаим  топологии). Более того, иногда (очень редко) мы даже не знаем можно ли при даном техническом уровне ее вообще реализовать :) Чаще всего решений построения цепи может быть очень-много (нас ограничивает только наша фантазия и знания). Между многими решениями мы выбираем то, которое больше всего подходит нам по финансам, элементной базе, массе и габаритам.  Реже всего решений может вообще не быть (если принципы роботы нашей цепи нарушают фундаментальные законы физики, а мы все же пытаемся ее создать =)).

     Для нас цепь, которую мы синтезируем, как чорный ящик, знаем что поступает на вход цепи, знаем что должно быть на выходе, а что происходить внутри пока неизвестно. Но и задачи синтеза в большинства случаев, при наличии смекалки, вполне выполнимы.

 

     Рис. 2 Модель єлектрической схемы которую нужно синтезировать (создать)

     Задачи синтеза электрических цепей значительно упрощаются если использовать схемный подход. Например, во многих зарубежных компаниях-бренадах электроники есть своя база (или банк, называйте как хотите) схемотехнических решений. Таких решений может быть очень много (вполоть до нескольких миллионов). И вы, например, как сотрудник такой компании имеете к ним доступ. Таким образом вам, в большинстве случаев, ненадо ничего нового придумывать, вы используете уже готовые схемные решения (и методики расчета к ним), естественно коректируете расчеты под вашу задачу, если нужно объединяете несколько уже готовых схемотехнических решений, и успешно этим самым синтезируете новую электрическую цепь для ваших нужд. К сожалению, компании стран СНГ редко используют даную методику.

   При синтезе цыфрових логических схем используют уже хорошо наработаные методы дискретной математики (булевая алгебра, минимизация логических функций и т.д.). 

      При синтезе аналоговых цепей используют два направления синтеза:

1) по известным операторным функциям, по Z(p) для двухполюсников и по передаточной функции для четырехполюсников;

2) по временным характеристикам, т.е. по известному временному отклику системы при воздействии импульса, обычно прямоугольной формы.

11. Графическое изображение синусоидальных величин.

Для сравнения электрических величин, изменяющихся по синусоидальному закону, необходимо знать разность их начальных фаз. Если, например, на каком - либо участке ток i и напряжение u имеют одинаковые начальные фазы, говорят, что они совпадают по фазе. Если график изменения во времени напряжения u на каком-либо участке цепи пересекает координату времени t раньше графика тока i, то говорят, что напряжение по времени опережает ток.

Н а рис. 3.2 для заданного элемента цепи представлены графики изменения во времени двух электрических величин: напряжения u и тока i. Из этих двух графиков видно, что они сдвинуты по фазе друг относительно друга на угол φ.

u

Аналитическая форма представления

I = Im·sin(ω·t + ψi), u = Um·sin(ω·t + ψu), e = Em·sin(ω·t + ψe),

где I, u, e – мгновенное значение синусоидального тока, напряжения, ЭДС, т. е. Значения в рассматриваемый момент времени;

Im, Um, Em – амплитуды синусоидального тока, напряжения, ЭДС;

(ω·t + ψ) – фазовый угол, фаза; ω = 2·π/Т – угловая частота, характеризующая скорость изменения фазы;

ψi, ψu, ψe – начальные фазы тока, напряжения, ЭДС отсчитываются от точки перехода синусоидальной функции через нуль к положительному значению до начала отсчета времени (t = 0). Начальная фаза может иметь как положительное так и отрицательное значение.

12. В цепях переменного тока широко используют т.н. действующие значения. Понятие действующего значения определяется из условия равенства теплового эффекты переменного и постоянного токов. Пусть через некоторый участок электрической цепи с сопротивлением r протекает переменный ток i. Тогда по закону Джоуля-Ленца на этом участке за время T, соответствующее периоду тока i, будет выделено количество тепла равное

Обозначим через I некоторый постоянный ток, при протекании которого по тому же участку цепи за время T выделится такое же количество тепла. Тогда с учетом того, что i = Imsin(wt+yi) получим: т.е. величина постоянного тока эквивалентного переменному току по количеству выделяемого тепла называется действующим или среднеквадратичным значением переменного тока. Как следует из выражения (2), действующее и амплитудное значения синусоидального тока связаны между собой постоянным коэффициентом.

По аналогии с током действующие значения вводятся для напряжений и ЭДС Действующие значения обозначаются прописными буквами без индекса.

Кроме действующих значений для синусоидальных величин иногда используются также средние значения. Под средним значением любой величины за интервал времени от t1 до t2 понимается

Но интеграл от синусоидальной функции за период равен нулю, поэтому для определения среднего значения используют интервал времени в половину периода. Тогда для тока получим:

Для напряжений и ЭДС средние значения определятся аналогично

13. При расчете электрических цепей часто приходится складывать или вычитать величины токов или напряжений, являющиеся синусоидальными функциями времени. Графические построения или тригонометрические преобразования в этом случае могут оказаться слишком громоздкими.       Задача  упрощается, если  представить наши синусоидальные функции в векторной форме. Имеем синусоидальную функцию  . Известно, что проекция отрезка, вращающегося вокруг оси с постоянной угловой скоростью, на любую линию, проведенную в плоскости вращения, изменяется по синусоидальному закону.

     Пусть отрезок прямой длиной I_m начинает вращаться вокруг оси 0 из положения, когда он образует с горизонтальной осью угол φ, и вращается против часовой стрелки с постоянной угловой скоростью ω. Проекция отрезка на вертикальную ось в начальный момент времени  . Когда отрезок повернется на угол α₁, проекция его  . Откладывая углы α₁, α₂, ... на горизонтальной оси, а проекции отрезка прямой - на вертикальной оси, получим ряд точек синусоиды (рис. 6.1).

       Пусть даны два синусоидальных тока:   и

                           .

       Нужно сложить эти токи и получить результирующий ток:

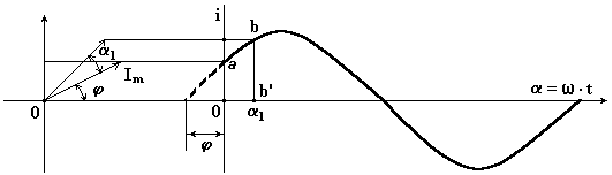Рис. 6.1

       Представим синусоидальные токи i₁ и i₂ в виде двух радиус - векторов, длина которых равна в соответствующем масштабе I_1m и I_2m. Эти векторы расположены в начальный момент времени под углами φ₁ и φ₂ относительно горизонтальной оси. Сложим геометрически отрезки I_1m и I_2m. Получим отрезок, длина которого равна амплитудному значению результирующего тока I_3m. Отрезок расположен под углом φ₃ относительно горизонтальной оси. Все три отрезка вращаются вокруг оси 0 с постоянной угловой скоростью ω. Проекции отрезков на вертикальную ось изменяются по синусоидальному закону. Будучи остановленными для рассмотрения, данные отрезки образуют векторную диаграмму (рис. 6.2).        Векторная диаграмма - это совокупность векторов, изображающих синусоидальные напряжения, токи и ЭДС одинаковой частоты.

     Необходимо отметить, что напряжение, ток и ЭДС - это скалярные, а не векторные величины.       Мы представляем их на векторной диаграмме в виде не пространственных, а временных радиус - векторов, вращающихся с одинаковой угловой скоростью.      Изображать на векторной диаграмме два вектора, вращающихся с различной угловой скоростью, бессмысленно.

                 Рис. 6.2         Положительным считается направление вращения векторов против часовой стрелки.        Векторные  диаграммы  используются  для  качественного анализа электрических цепей, а также при решении некоторых электротехнических задач.

При расчетах цепей синусоидального тока используют символический метод расчета или метод комплексных амплитуд. В этом методе сложение двух синусоидальных токов заменяют сложением двух комплексных чисел, соответствующих этим токам.       Из курса математики известно, что комплексное число может быть записано в показательной или алгебраической форме:

         где с - модуль комплексного числа;                 φ- аргумент;                 a - вещественная часть комплексного числа;                 b - мнимая часть;                 j - мнимая единица, j = √-1.

      С помощью формулы Эйлера можно перейти от показательной формы записи к алгебраической.

             

      От алгебраической формы записи переходят к показательной форме с помощью формул:

       

      Комплексное число может быть представлено в виде радиус - вектора в комплексной плоскости. Вектор длиной, равной модулю c, расположен в начальный момент времени под у глом φ относительно вещественной оси (рис.6.3).

     Умножим комплексное число на множитель  .       Радиус - вектор на комплексной плоскости повернется на угол β.       Множитель   называется поворотным.                                           Рис.6.3

      Если  , то вектор, умноженный на  , превратится во вращающийся со скоростью ω радиус - вектор.         Выражение   называется комплексной функцией времени.      Применительно к напряжению, получим   - комплексную функцию времени для напряжения.           - комплексная амплитуда напряжения (исходное положение вектора в комплексной плоскости). Определим, чему равна мнимая часть комплексной функции времени для напряжения.

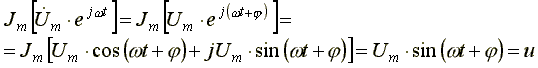
    Мгновенное синусоидальное напряжение (ток, ЭДС) является мнимой частью соответствующей комплексной функции времени.

    Замечание. В электротехнике над символами, изображающими комплексные напряжения, токи, ЭДС, принято ставить точку.      Синусоидальные функции времени могут быть представлены векторами в комплексной плоскости, вращающимися против часовой стрелки с постоянной угловой скоростью ω. Проекция вектора на мнимую ось изменяется по синусоидальному закону.