37. Оценка ожидаемого эффекта от проекта при вероятностной неопределенности.

При вероятностной неопределенности по каждому сценарию считается известной (заданной) вероятность его реализации. Она мо­жет определяться экспертно. Вероятностное описание условий реализации проекта оправданно и применимо, когда эффективность проекта обусловлена, прежде всего, неопределенностью процессов эксплуатации и износа ос­новных средств (снижением прочности конструкций зда­ний и сооружений, отказами оборудования и т.п.) или природно-климатических условий (погоды, характеристик грунта или запасов полезных ископаемых, возможности землетрясений или наводнений и т.п.), а также неопреде­ленностью изменений на рынке, имеющих отношение к инвестиционному проекту со стороны поставщиков, по­купателей, кредиторов и дебиторов, участвующих в фор­мировании денежных потоков; неустойчивостью рыноч­ной конъюнктуры, появлением новых конкурентов или товаров-заменителей на рынке, возможными колебания­ми финансовых результатов и финансовой устойчивости, относящихся к проекту. С определенной долей условно­сти колебания дефлированных цен на производимую продукцию и потребляемые ресурсы могут описываться также в вероятностных терминах.

• Следует учитывать, что колебания цен на разные ви­ды товаров взаимозависимы. Поэтому, например, из то­го, что цены на бензин и на автомобильные перевозки с большой вероятностью могут отклоняться от средних на 10%, не следует, что с большой вероятностью одна из этих цен упадет на 10%, а другая вырастет на 10%.

Когда имеется конечное количество сценариев и вероят­ности их заданы, ожидаемый интегральный эффект проекта рассчитывается по формуле математического ожидания

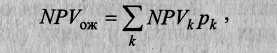
где NPVk — интегральный эффект (ЧДД) для k-го сценария; p_k — вероятность реализации этого сценария.

При этом риск неэффективности проекта Рэ и сред­ний ущерб от реализации проекта в случае его неэффек­тивности Уэ определяются по формулам

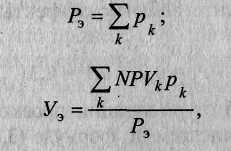
где суммирование ведется только по тем k сценариям, для которых интегральные эффекты (ЧДД) NPVk отрицательны.

Для упрощения средний ущерб Уэ от реализации проекта в случае его неэффективности условимся назы­вать средним возможным ущербом.

Интегральные эффекты сценариев NPVk и ожидаемый эффект NРV_ОЖ зависят от нормы дисконта r. Премия g за риск неполучения доходов, предусмотренных основным сценарием проекта, определяется из условия равенства между ожидаемым эффектом проекта NPVо_ж (r), рассчитанным при безрисковой норме дисконта r, и эффектом основного сценария NPV_0C (r + g), рассчитанным при норме дисконта (r + g), включающей поправку на риск g

В этом случае средние потери от неполучения преду­смотренных основным сценарием доходов при неблаго­приятных сценариях покрываются средним выигрышем от получения более высоких доходов при благоприятных сценариях.

Размер премии g зависит от того, какой сценарий принят в качестве основного. При отсутствии информации о вероятностях отдельных сценариев для упрощения оценки эффективности рекомендуется использовать в этом сценарии умеренно пессимистические, а не сред­ние оценки расходов и доходов, т.е. ориентироваться на сниженный размер премии за риск.

Предположим, что процесс функционирования объекта рассматривается как дискретный и начинается с 1-го шага (года). Срок службы объекта не ограничен. На каждом n-м шаге объект обеспечивает получение неслучайного (годо­вого) эффекта Ф_0n= FVn – 3n. В то же время проект пре­кращается на некотором шаге, если на этом шаге происхо­дит «катастрофа» (резкое ухудшение результатов работы инвестиционного проекта, обусловленное появлением на, рынке более дешевого продукта-заменителя, серьезной аварией оборудования, стихийным бедствием и т.д.). Ве­роятность того, что катастрофа произойдет на некотором шаге при условии, что ее не было на предыдущих шагах, не зависит от номера шага и равна р. Ожидаемый инте­гральный эффект здесь определяется следующим образом. Отметим, что вероятность того, что на 1-м шаге «катастрофы» не произойдет, равна (1—p). Вероятность того, что она не произойдет ни на первом, ни на втором шаге, по правилу произведения вероятностей равна (1 - р)² и т.д. Поэтому либо до конца n-го шага «катастрофы» не про­изойдет и эффект проекта на этом шаге будет равен Ф_0n либо такое событие произойдет и тогда этот эффект будет равен нулю. Сказанное означает, что математическое ожидание (среднее значение) эффекта на данном п-м шаге будет равно Фо_п(1—р)ⁿ. Суммируя эти величины с учетом разновременности, найдем математическое ожидание NPV проекта:

Из полученной формулы видно, что разновременные эффекты Ф_0n обеспечиваемые «в нормальных условиях», т.е. при отсутствии катастроф, приводятся к базовому моменту времени с помощью коэффициента (1 — р)^п / (1 + r)ⁿ, не совпадающего с «обычным» ко­эффициентом дисконтирования 1/(1 + r)^п. Для того чтобы «обычное» дисконтирование без учета факторов риска и расчет с учетом этих факторов дали один и тот же результат, необходимо, чтобы в качестве нормы дис­конта было принято иное значение r_р, такое, что 1 + r_p = (1 +r) / (1 — р). Отсюда получаем, что г_р = (r + р): (1 — р). При малых значениях вероятности р эта фор­мула принимает вид г_р = r + р, подтверждая, что в дан­ной ситуации учет риска сводится к расчету NPV «в нормальных условиях», но с нормой дисконта r_p пре­вышающей безрисковую r на размер «премии за риск», отражающей в данном случае (условную) вероятность прекращения проекта р в течение соответствующего года п. Использование такого метода в других ситуациях рас­смотрено выше.