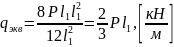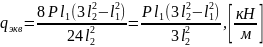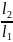- •Железобетонные плоские перекрытия. Классификация перекрытий.
- •Монолитные ребристые перекрытия с балочными плитами
- •Расчет плиты перекрытия
- •Расчет неразрезного ригеля
- •Балочные панельные сборные перекрытия.
- •Расчет сплошных плит (панелей).
- •Расчет и конструирование панелей с круглыми пустотами.
- •Расчет плит с овальными пустотами.
- •Расчет и конструирование ребристых плит.
- •Армирование ребристой плиты.
- •Соединение сборного ригеля с колонной.
- •Монолитные ребристые перекрытия с плитами, опертыми по контуру.
- •Безбалочные капительные перекрытия.
- •Сборно-монолитные безбалочные капительные перекрытия.
- •Монолитные безбалочные капительные перекрытия.
- •Армирование монолитного безбалочного перекрытия.
- •Монолитные безбалочные бескапительные перекрытия.
- •Расчет на продавливание железобетонных элементов без поперечной арматуры при действии сосредоточенной силы.
- •Расчет элементов без поперечной арматуры на продавливание при совместном действии сосредоточенных сил и изгибающего момента.
Расчет плит с овальными пустотами.
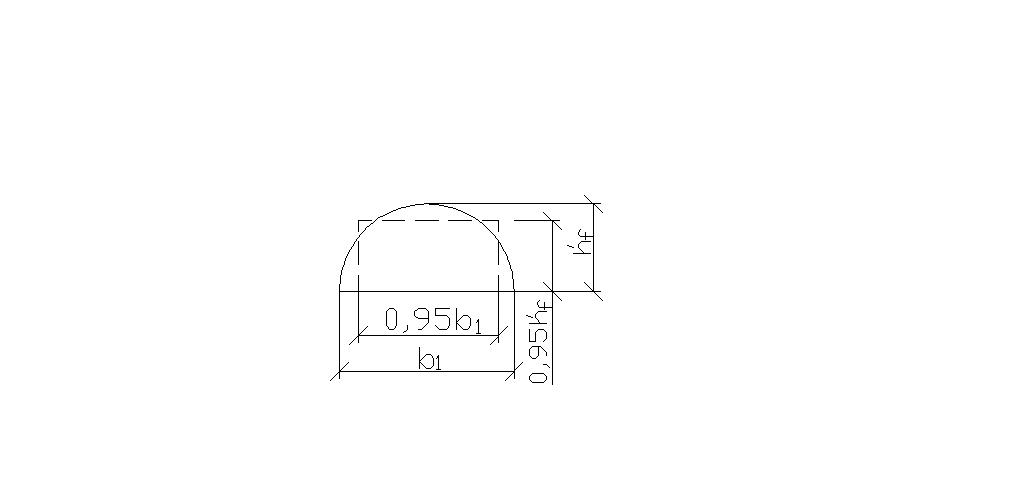
Для панелей с овальными пустотами овальное сечение заменяют прямоугольным с той же площадью.
Расчет и конструирование ребристых плит.
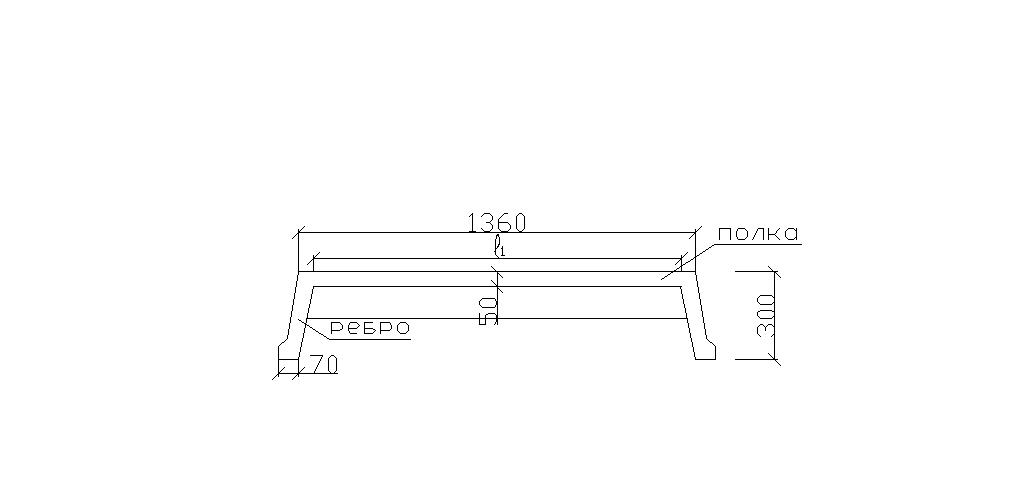
Расчет
плиты начинают с расчета полки. При
отсутствии промежуточных ребер полку
плиты можно рассчитывать как балку,
частично защемленную на опорах пролетом
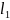 .
Для этого мысленно вырезаем полосу
шириной 1м и рассматриваем ее как балку,
частично защемленную на опорах пролетом
,
на которую действует равномерно
распределенная нагрузка.
.
Для этого мысленно вырезаем полосу
шириной 1м и рассматриваем ее как балку,
частично защемленную на опорах пролетом
,
на которую действует равномерно
распределенная нагрузка.
Эпюра изгибающих моментов имеет вид:
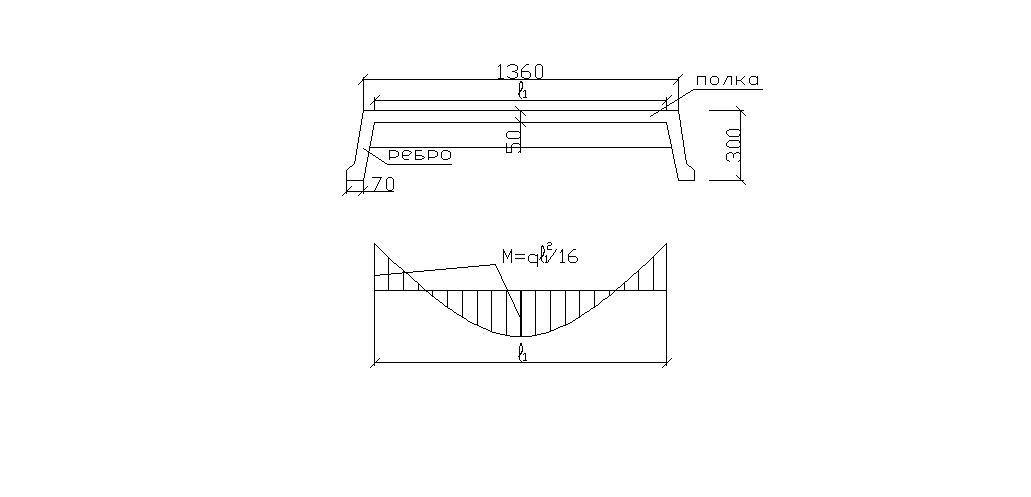
Расчет прочности продольных ребер плиты сводится к расчету таврового сечения с полкой в сжатой зоне. При расчете прочности по изгибающему моменту ширина ребра равна суммарной ширине двух ребер плиты.
Р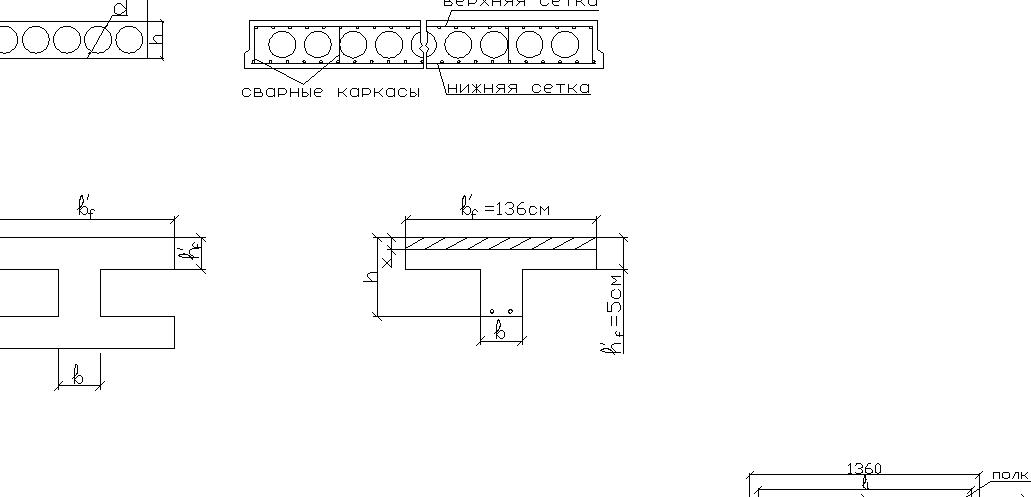 асчетная
ширина полки принимают равной:
асчетная
ширина полки принимают равной:
при

при .
Расчетная
высота полки
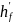 принимается равной толщине плиты
принимается равной толщине плиты
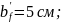
Изгибающий момент в балке
Поперечная сила в балке
Полученную площадь сечения продольной рабочей арматуры распределяют на два ребра. К концам продольной ненапрягаемой арматуры ребристых плит приваривают анкеры из уголков или пластин для закрепления стержней на опоре.
При наличии промежуточных ребер полку ребристой плиты рассчитывают как полку, опертую по четырем сторонам, на которую действует треугольная распределенная нагрузка.
Аналогично рассчитывают поперечные ребра плиты как балку таврового сечения на треугольную нагрузку.
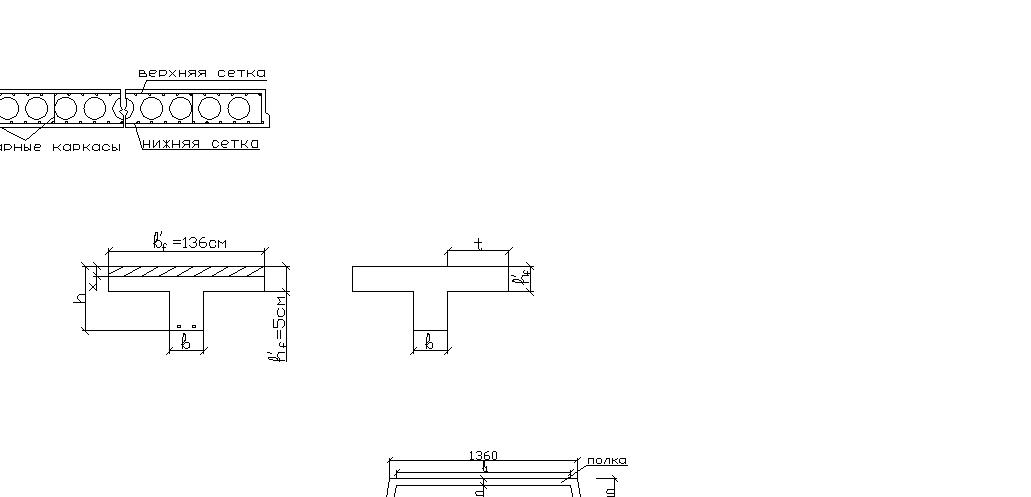
Ширину
свеса полки в каждую сторону от ребра
принимают t=
 .
.
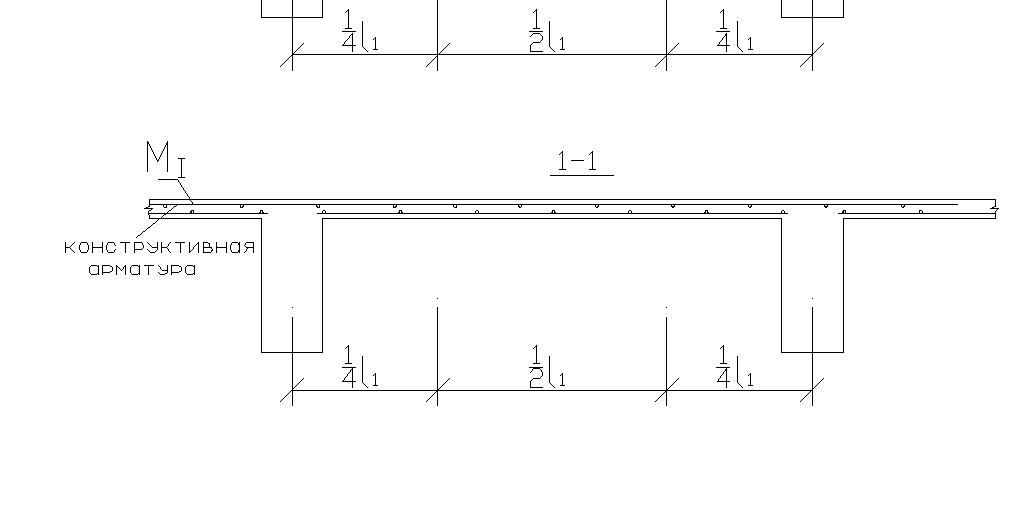
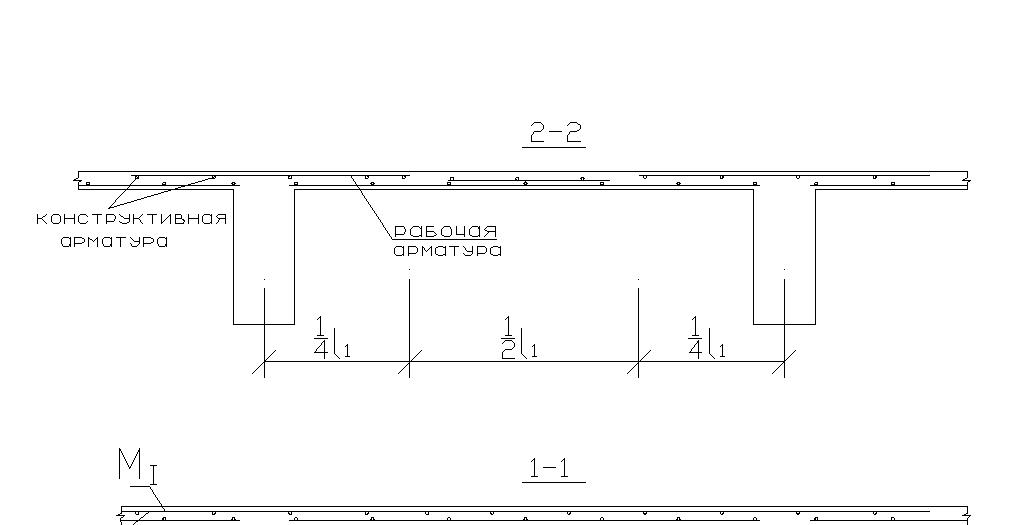
Армирование ребристой плиты.
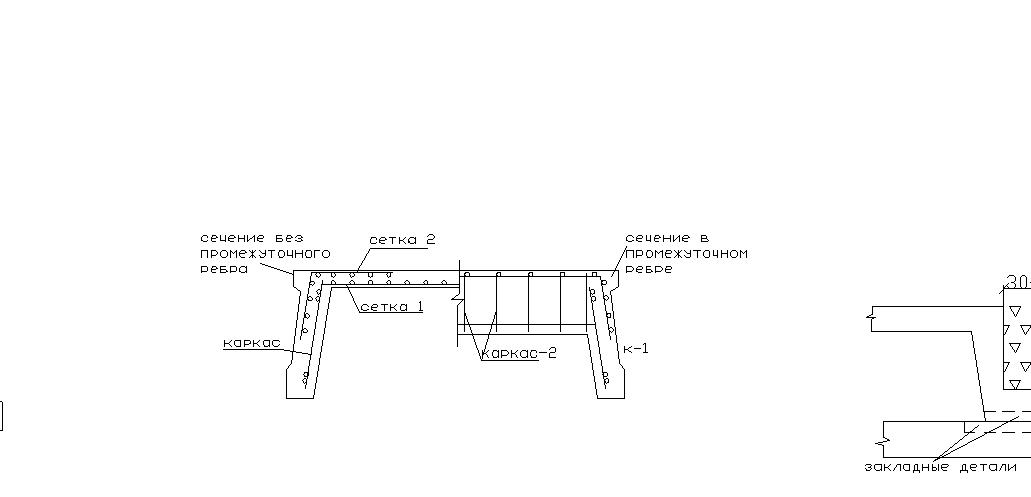
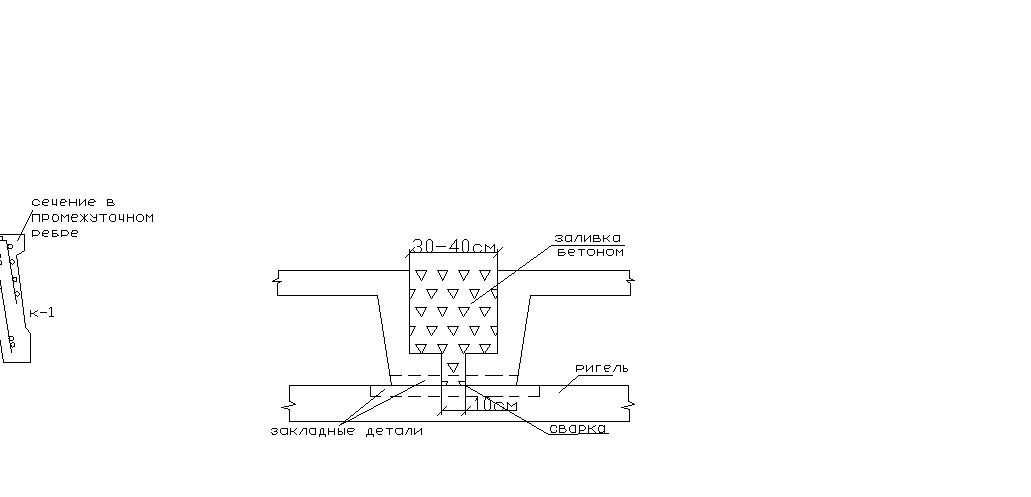
Сетка 2 воспринимает опорный момент панелей плиты, сетка 1 – пролетный момент панелей плиты. Каркас 1 воспринимает изгибающий момент, действующий в продольных ребрах плиты. Каркас 2 воспринимает изгибающие моменты, поперечные силы, действующие в промежуточных ребрах плиты.
Соединение сборного ригеля с колонной.
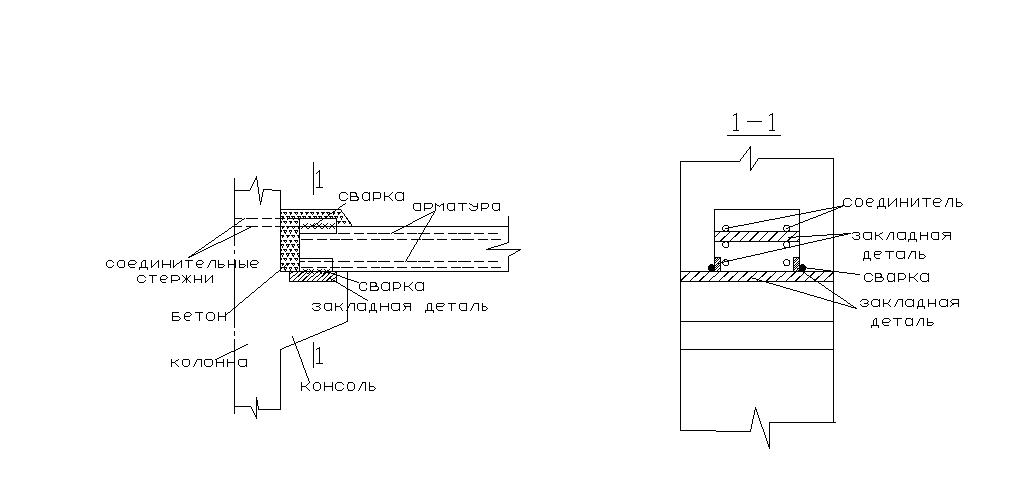
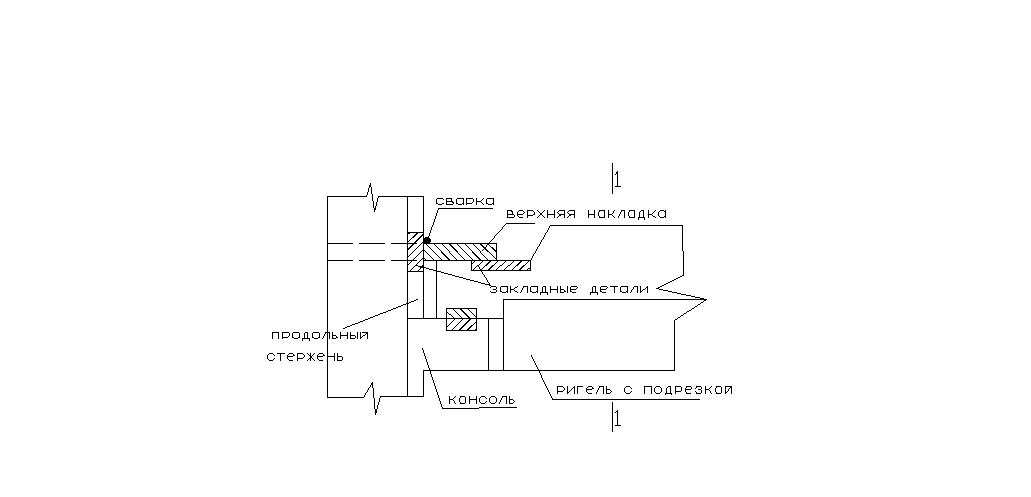
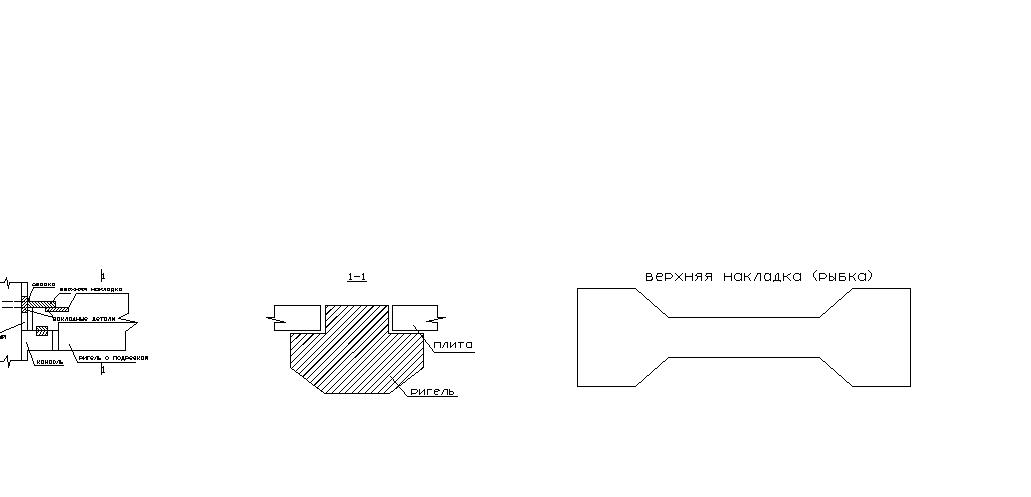
В жилых и общественных зданиях соединение ригеля с колонной по первому варианту не применяется, а только в производственных зданиях, поэтому в административных и общественных зданиях для соединения ригеля с колонной в сборном варианте применяют следующее конструктивное решение: Консоль колонны имеет прямоугольное сечение, а сборный ригель с подрезкой, то есть его высота сечения в месте опирания на консоль меньше чем в пролете. Сечение ригеля имеет форму, представленную на рисунке, и позволяет опирать плиты перекрытия на кромки ригеля. Это приводит к сокращению или уменьшению толщины перекрытия.
К вертикальной арматуре колонны приваривается верхняя накладка, которая имеет форму рыбки, причем ширина пластины- рыбки рассчитывается таким образом, чтобы опорный узел воспринимал опорный изгибающий момент 55 кНм. К верхней арматуре ригеля приваривается также закладная деталь, которая сваривается с верхней накладкой.
Восприятие момента 55 кНм необходимо для обеспечения устойчивости колонны при односторонней укладке плит перекрытия.
Монолитные ребристые перекрытия с плитами, опертыми по контуру.
П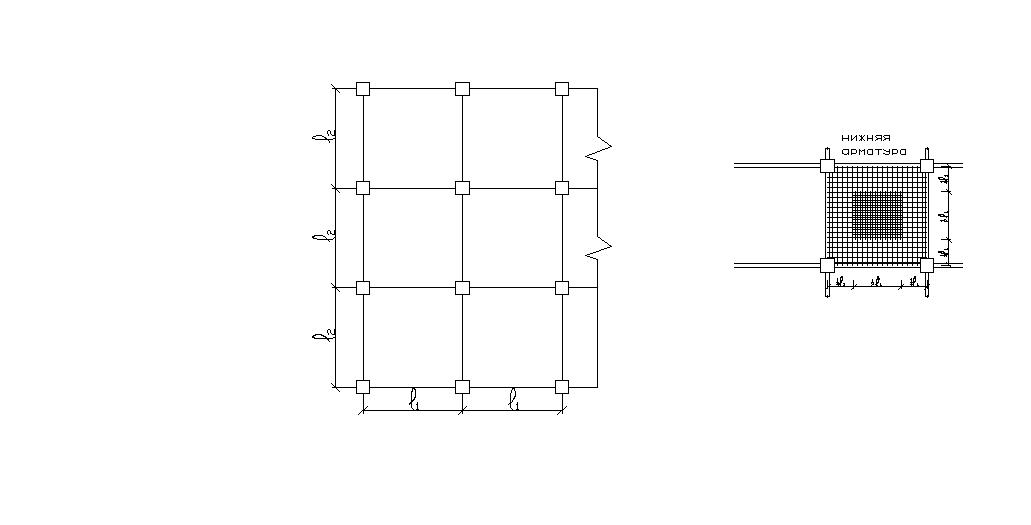 ерекрытие
состоит:
ерекрытие
состоит:
плит, работающих в двух направлениях;
поддерживающих их ригелей, расположенных в двух направлениях, и опирающихся на колонны или стены.
Перекрытия
применяются
в основном для перекрытия залов и
вестибюлей в общественных зданиях.
Соотношение стороны плиты колеблется
от 1 1,5.
Толщина плиты перекрытия принимается
в пределах от 50 – 160 мм, но не менее
1,5.
Толщина плиты перекрытия принимается
в пределах от 50 – 160 мм, но не менее
 (
(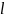 -
максимальный пролет).
По расходу материала перекрытия с
плитами, опертых по контуру, менее
экономично по сравнению с перекрытиями
с балочными плитами.
-
максимальный пролет).
По расходу материала перекрытия с
плитами, опертых по контуру, менее
экономично по сравнению с перекрытиями
с балочными плитами.
Монолитные ребристые перекрытия с плитами, опертыми по контуру, могут быть рассчитаны по упругой теории и по методу предельного равновесия. По упругой теории рассчитывают плиты, в которых не допускаются трещины. Если трещины в перекрытии допускаются, расчет ведут по методу предельного равновесия.
Пластические шарниры в плите перекрытия образуются в нижней зоне посередине пролета и по биссектрисам углов, в верхней зоне- вдоль контура опирания и закругления в углах.
Р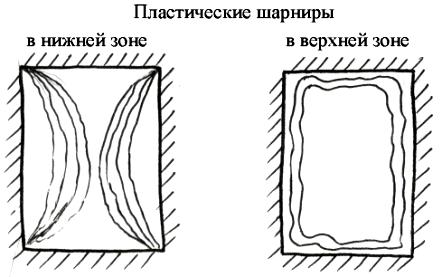 ассмотрим
расчет перекрытия по методу предельного
равновесия.
ассмотрим
расчет перекрытия по методу предельного
равновесия.
П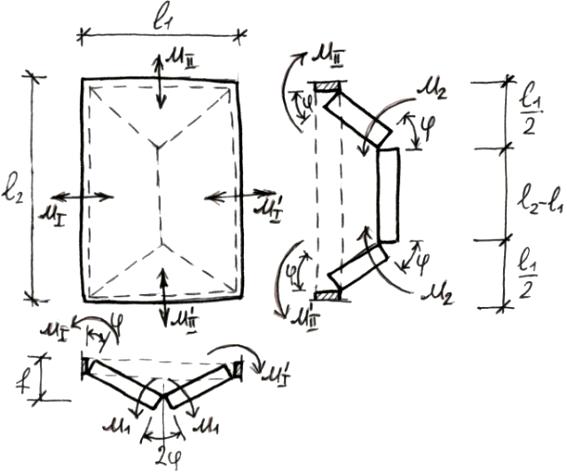 о
методу предельного равновесия плита
представляется в виде системы плоских
звеньев, связанных между собой линейными
пластическими шарнирами. Согласно
принципам возможных перемещений
(Лагранжа): если система находится в
равновесии, то на любом возможном
бесконечно малом перемещении работа
внешних сил равна работе внутренних
сил:
о
методу предельного равновесия плита
представляется в виде системы плоских
звеньев, связанных между собой линейными
пластическими шарнирами. Согласно
принципам возможных перемещений
(Лагранжа): если система находится в
равновесии, то на любом возможном
бесконечно малом перемещении работа
внешних сил равна работе внутренних
сил:
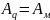 (1)
(1)
Внешняя нагрузка в связи с этим с перемещением плиты совершает работу, равную произведению интенсивности нагрузки (q) на объем фигуры перемещения:
 (2)
(2)
Объем
фигуры (плиты):
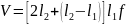
Работа внутренних сил равна произведению шести изгибающих моментов на соответствующей ширине, на угол поворота.
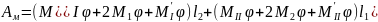 (3).
(3).
Приравнивая уравнение (2) и (3), получим:
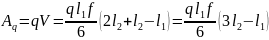
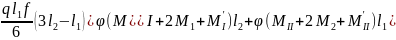 (4).
(4).
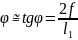 (5).
(5).
Подставляя уравнение (5) в (4), получим:
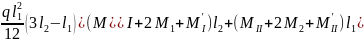 (6).
(6).
Уравнение (6) применяется при армировании в нижней зоне одной сеткой стержней.
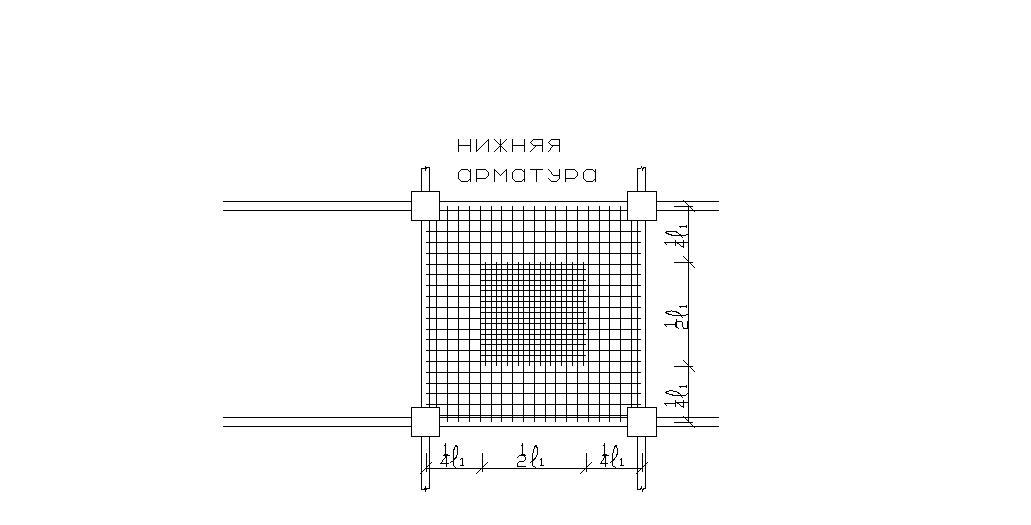
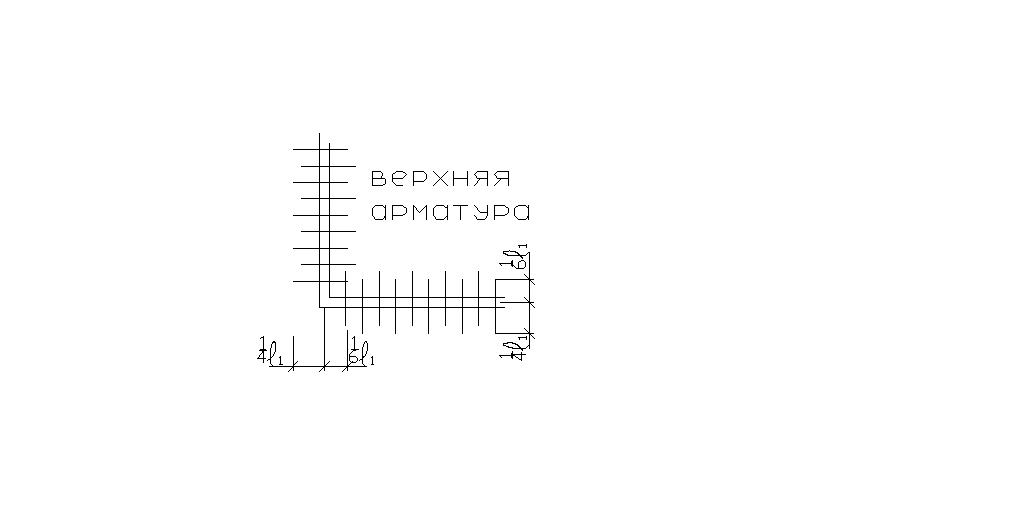
Если
одна из нижних сеток плиты не доходит
до опоры на
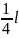 ,
площадь нижней рабочей арматуры,
пересеченной линейным пластическим
шарниром в краевой полосе, будет вдвое
меньше, и уравнение (6) примет другой
вид:
,
площадь нижней рабочей арматуры,
пересеченной линейным пластическим
шарниром в краевой полосе, будет вдвое
меньше, и уравнение (6) примет другой
вид:
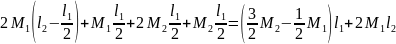
Подставляем
в уравнение (6) вместо
 и
и
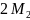 :
:
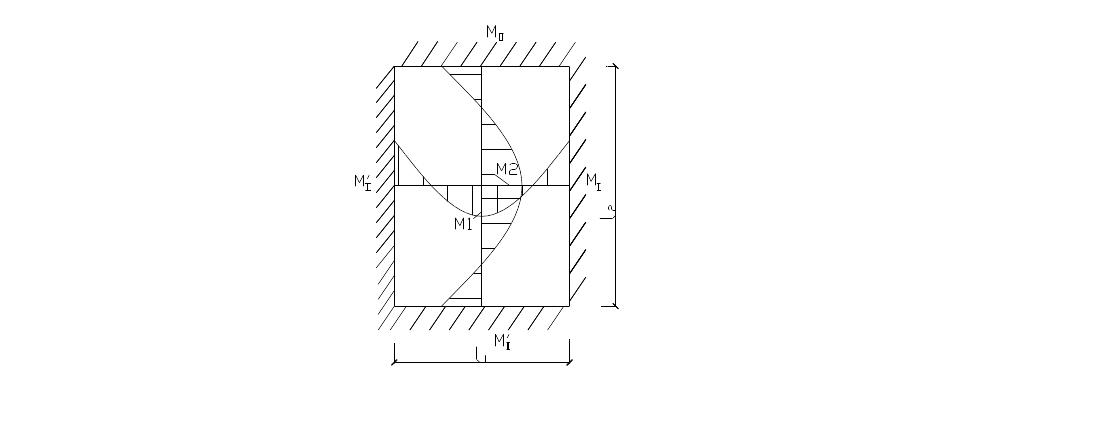
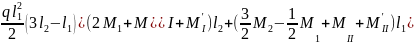 (7).
(7).
Выражение (7) служит для определения изгибающих моментов в плите при армировании в нижней зоне двумя сетками.
В уравнении (7) шесть неизвестных.
Изгибающие моменты в плите, в направлении короткого пролета, будут больше, чем в направлении большего пролета.
|
1 |
1,1 |
1,2 |
1,3 |
1,4 |
1,5 |
1,6 |
1,7 |
1,8 |
1,9 |
2 |
3 |
|
1
0,8 |
0,9
0,7 |
0,8
0,6 |
0,7
0,5 |
0,6
0,4 |
0,55
0,35 |
0,5
0,3 |
0,45
0,25 |
0,4
0,2 |
0,35
0,2 |
0,3
0,0,15 |
0,15
0 |
Зная
соотношение размеров пролетов, по
таблице назначаем соотношение
и выражаем
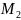 через
через
 .
Далее по экономическим и конструктивным
соображениям назначаем соотношения
опорных моментов к пролетным:
.
Далее по экономическим и конструктивным
соображениям назначаем соотношения
опорных моментов к пролетным:
 и выражаем опорные моменты через
и выражаем опорные моменты через
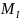 .
.
Пример.
 (а);
(а);
 (б)
(б)
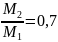
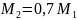 (в);
(в);
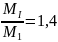 ;
;
 (г)
(г)
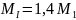 ;
;
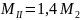 ;
;
 (д).
(д).
Подставляем уравнения (а)-(д) в уравнение (7) получаем . Зная , из уравнений (а)-(д) находим остальные изгибающие моменты.
Строим
эпюры изгибающих моментов в основных
сечениях. Задаваясь толщиной плиты,
площадь сечения арматуры в направлении
каждого пролета определяем как в балке
шириной b=100см
и высотой, равной толщине плиты
 .
Назначая шаг стержней, определяем число
стержней
.
Назначая шаг стержней, определяем число
стержней
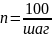 .
По таблице, зная
.
По таблице, зная
 и количество стержней на ширине 1м,
определяем диаметр стержней.
и количество стержней на ширине 1м,
определяем диаметр стержней.
На
изгибающий момент
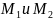 рассчитываем площадь сечения продольной
рабочей арматуры для двух сеток. Площадь
сечения арматур для одной сетки будет
равна
рассчитываем площадь сечения продольной
рабочей арматуры для двух сеток. Площадь
сечения арматур для одной сетки будет
равна
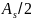 .
Опорная арматура в направлении пролетов
и
.
Опорная арматура в направлении пролетов
и
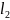 определяется по опорным моментам
определяется по опорным моментам
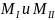 также как в балке шириной 100см и высотой
.
Размерность изгибающих моментов
также как в балке шириной 100см и высотой
.
Размерность изгибающих моментов
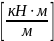 ,
нагрузки
,
нагрузки
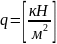 .
.
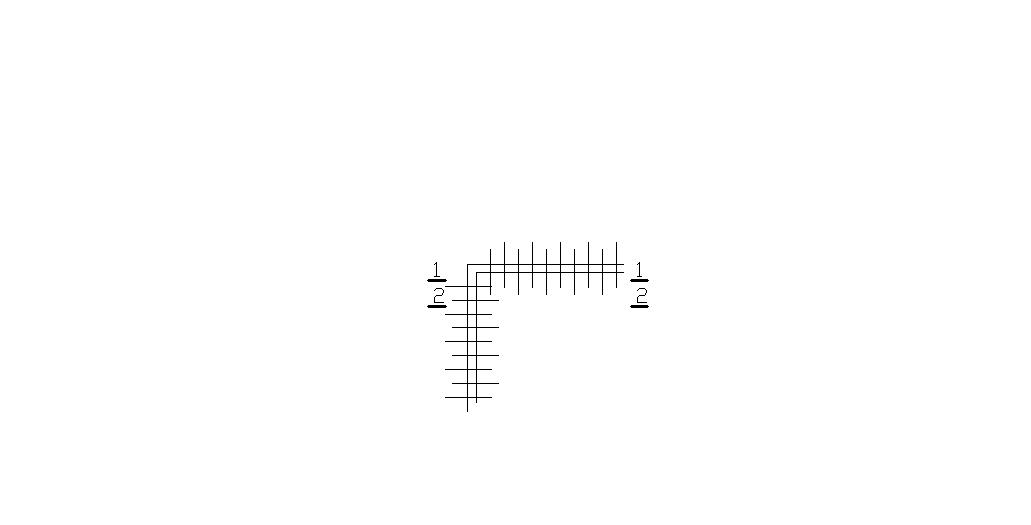
Если
плита опирается на стены свободно, то
одна из нижних сеток не доходит до опоры
на
 пролета.
пролета.
В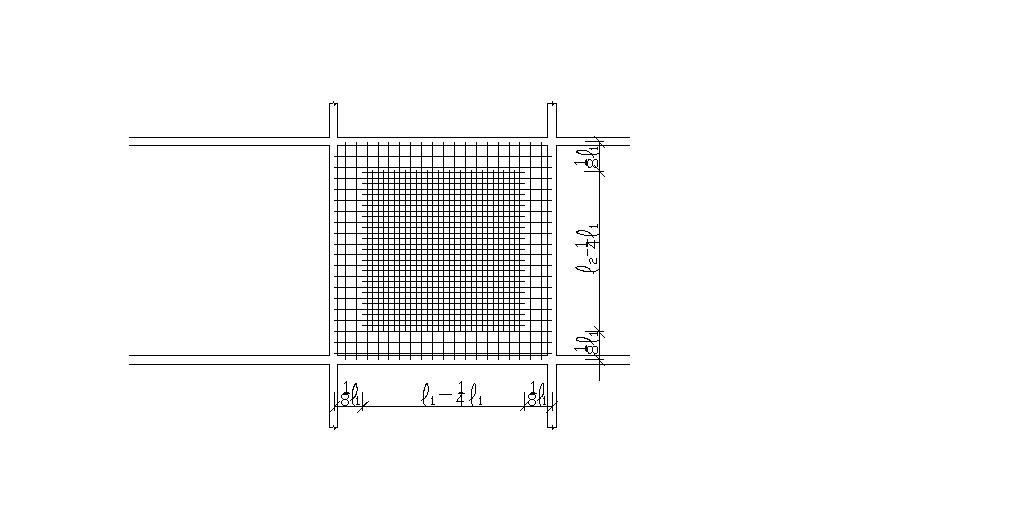 этом случае
этом случае
 (8)
(8)
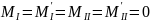
Пусть
на плиту действует равномерно
распределенная нагрузка Р
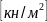
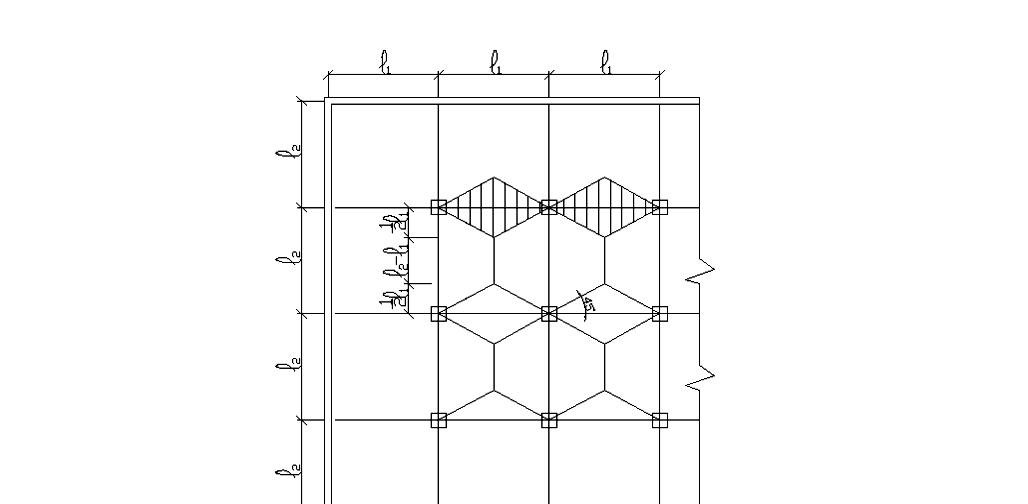 .
От плиты перекрытия на ригели нагрузка
передается под
.
От плиты перекрытия на ригели нагрузка
передается под
углом 45.
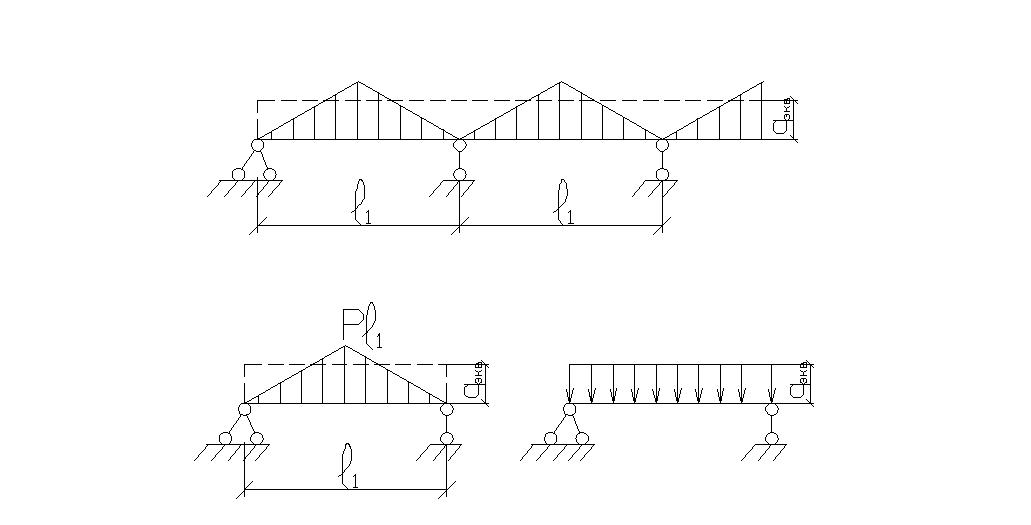
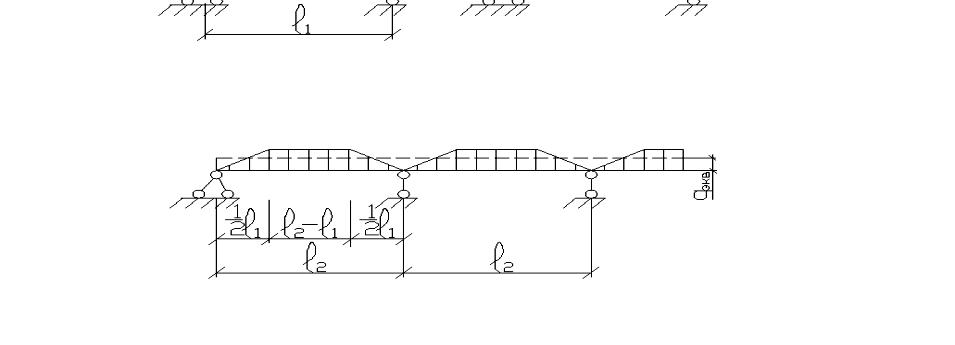
Если
пролет
 ,
то на ригели в направлении пролета
нагрузка передается по закону треугольника,
в направлении
- закону трапеции. Для упрощения расчета
неравномерно распределенную нагрузку
заменяют эквивалентной, по моменту в
однопролетной свободно опертой балке,
равномерно распределенной нагрузкой.
,
то на ригели в направлении пролета
нагрузка передается по закону треугольника,
в направлении
- закону трапеции. Для упрощения расчета
неравномерно распределенную нагрузку
заменяют эквивалентной, по моменту в
однопролетной свободно опертой балке,
равномерно распределенной нагрузкой.
При треугольной нагрузке.
 ;
;