Расчет неразрезного ригеля

В соответствие с нормами большую часть железобетонных конструкций, работающих в условиях статических нагрузок, следует рассчитывать с учетом перераспределения усилий, которое происходит вследствие пластических деформаций. При некотором значении нагрузки напряжение в растянутой арматуре из мягкой стали достигают предела текучести. С развитием текучести в арматуре в железобетонной конструкции возникает участок больших местных деформаций, называемый пластическим шарниром. Общим для обычного и пластического шарнира является то, что при возникновении любого из них конструкция теряет одну степень статической неопределимости или приобретает одну степень свободы. Это объясняется тем, что оба шарнира не препятствуют взаимному повороту сечений, где они возникли.

Пластический шарнир отличается от обычного шарнира по следующим признакам:

1. пластический шарнир является односторонним механизмом;

2. изгибающий момент в пластическом шарнире не равен нулю, а некоторому постоянному значению, которое соответствует несущей способности сечения, где он возник;

3. в статически определимой конструкции, например в однопролетной свободно опертой балке, с появлением пластического шарнира под влиянием взаимного поворота частей балки и большого прогиба напряжения в сжатой зоне растут, высота сжатой зоны уменьшается, и наступает разрушение.

Иначе себя ведет статически неопределимая конструкция. здесь с появлением пластического шарнира повороту частей балки, увеличению прогиба и росту напряжений в сжатой зоне препятствуют лишние связи (защемления на опорах). Поэтому при дальнейшем увеличении нагрузки разрушение не произойдет до тех пор, пока не появятся новые пластические шарниры, и не выключатся лишние связи. В статически неопределимой конструкции после появления пластического шарнира при дальнейшем увеличении нагрузки происходит перераспределение изгибающих моментов между отдельными сечениями.

Рассмотрим последовательность перераспределения изгибающих моментов на примере балки, защемленной на двух опорах.

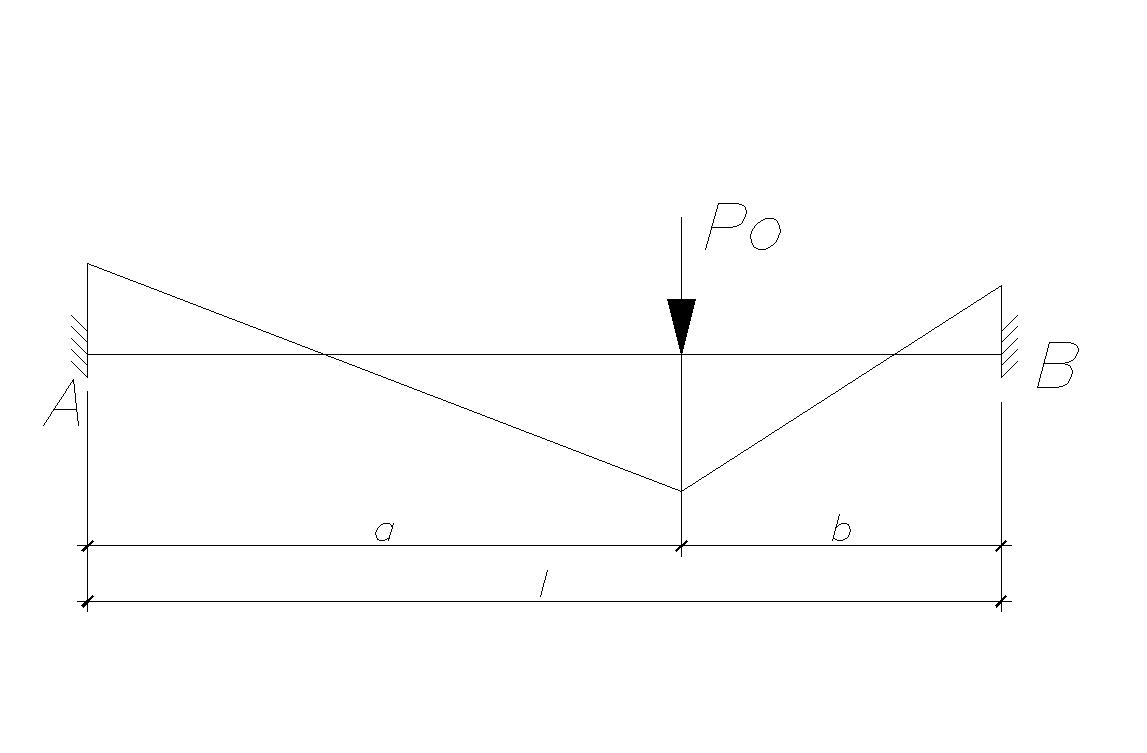
С появлением пластического шарнира на одной из опор при нагрузке Р₀ балка будет работать по новой схеме: одной защемленной и другой шарнирной опорах.

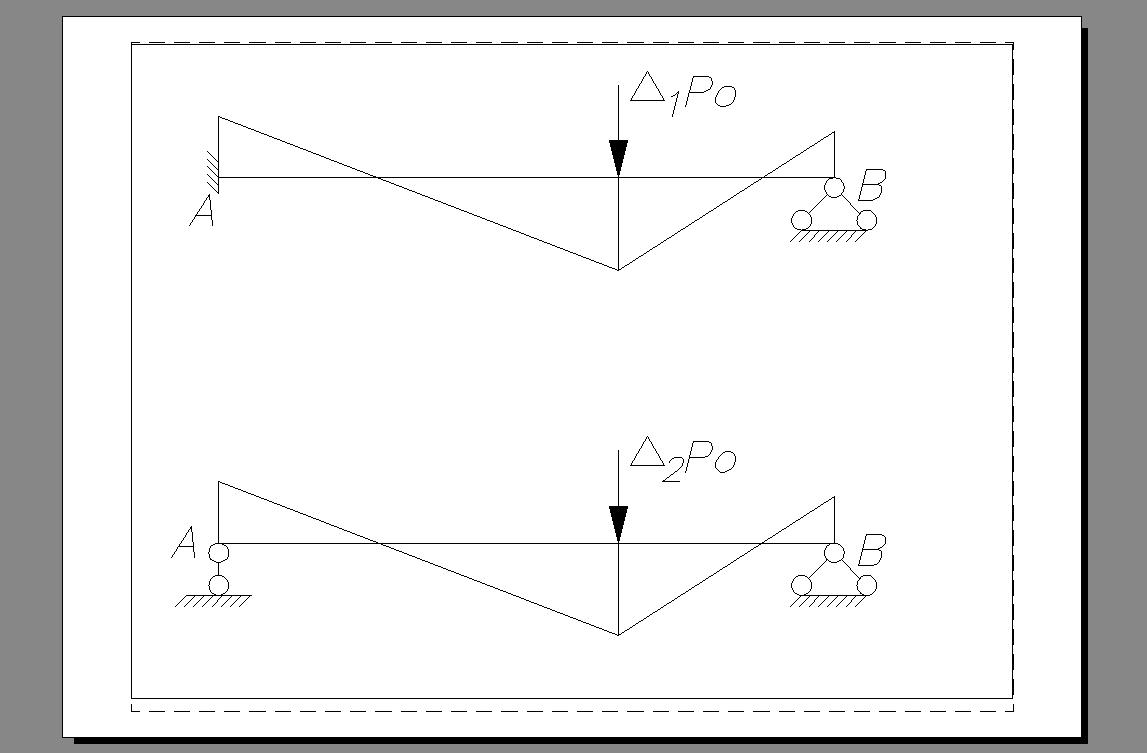
При дальнейшем увеличении нагрузки балка работает по новой схеме. С момента появления пластического шарнира на другой опоре балка превращается в свободно опертую.

Таким образом предельная сила будет равна:

предельные моменты в расчетных сечениях в пластических шарнирах М_А, М_В, М_пр. При предельном равновесии, то есть непосредственно перед разрушением, изгибающие моменты балки можно найти статическим или кинематическим способом.

Рассмотрим статический способ:

уравнение равновесия,

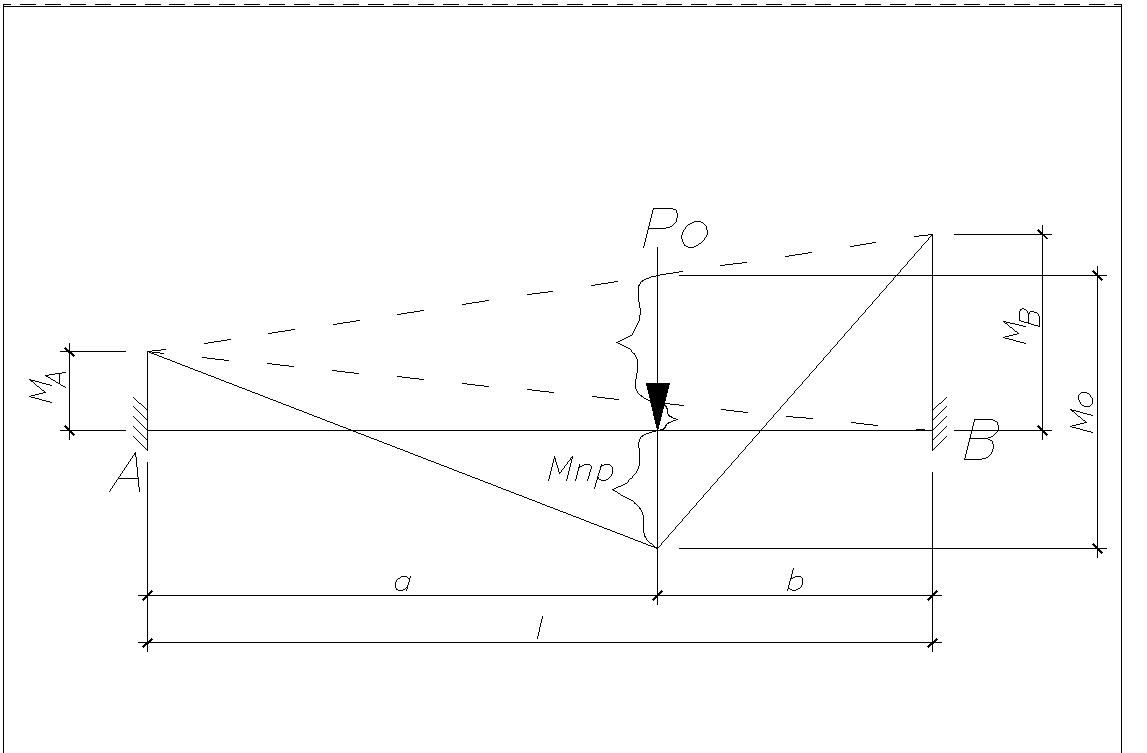
Уравнение показывает, что сумма пролетного момента и долей опорных моментов данном сечении равно моменту свободно опертой балки М₀. Из уравнения равновесия вытекает, что несущая способность статически неопределимой конструкции не зависит от последовательности образования пластических шарниров и не зависит от соотношения значений опорных и пролетных моментов.

Рассмотрим кинематический способ:

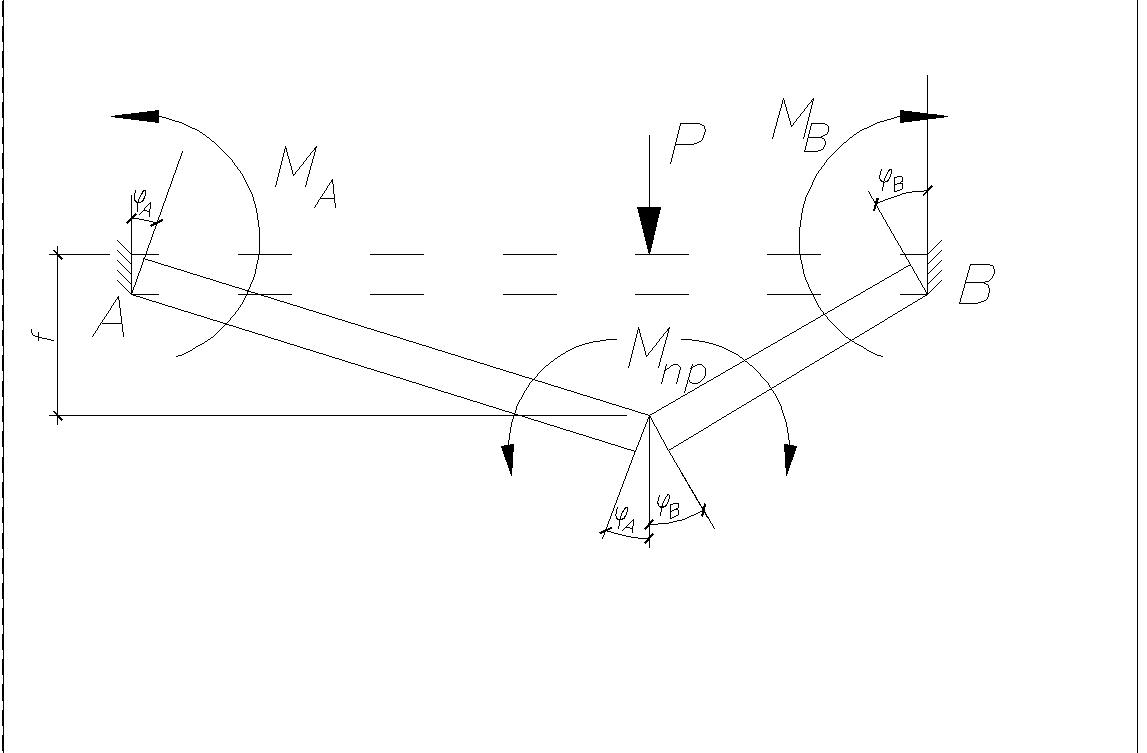
Балка в предельном равновесии рассматривается как система жестких плоских звеньев. соединенных между собой в местах излома пластическими шарнирами. Этот способ основан на принципе возможных перемещений (принципе Лагранжа), который гласит: если система находится в равновесии, то при всяком возможном бесконечно малом перемещении ее точек работа внешних сил равна работе внешних сил:

- работа внешних сил (1),

– работа внутренних сил (2),

Приравнивая (1) к (2), сокращая на f и умножая обе части неравенства на ab/l получим:

- уравнение равновесия.

Расчет и конструирование статически неопределимых железобетонных конструкций с учетом перераспределения усилий, то есть по выровненным моментам, позволяет:

1. облегчить армирование сечений, что очень важно для монтажных стыков на опорах сборных конструкций;

2. осуществлять одинаковое армирование сварными сетками и каркасами там, где при расчете по упругой схеме возникают различные по значению изгибающие моменты;

3. расчет при временных нагрузках по выровненным моментам по сравнению с расчетом по упругой схеме может давать до 30% экономии стали в арматуре;

4. ограничение раскрытия трещин в первых пластических шарнирах достигается ограничение выровненного момента не менее 70% момента в упругой схеме.

Для обеспечения возможности образования пластических шарниров необходимо соблюдать конструктивные требования:

• конструкция должна быть запроектирована так, чтобы причиной разрушения не был срез сжатого бетона;

• армирование сечений в местах образования пластических шарниров следует ограничивать так, чтобы относительная величина сжатой зоны не превышала 0,35 (ξ≤0,35)

• следует принимать армирующие стали, имеющие физический предел текучести, то есть площадку текучести.

Расчет железобетонных конструкций с учетом перераспределения усилий можно осуществлять только в статически неопределимых конструкциях и при действии временной нагрузки.

Расчет главной балки монолитного ребристого перекрытия с балочными плитами с учетом перераспределения усилий

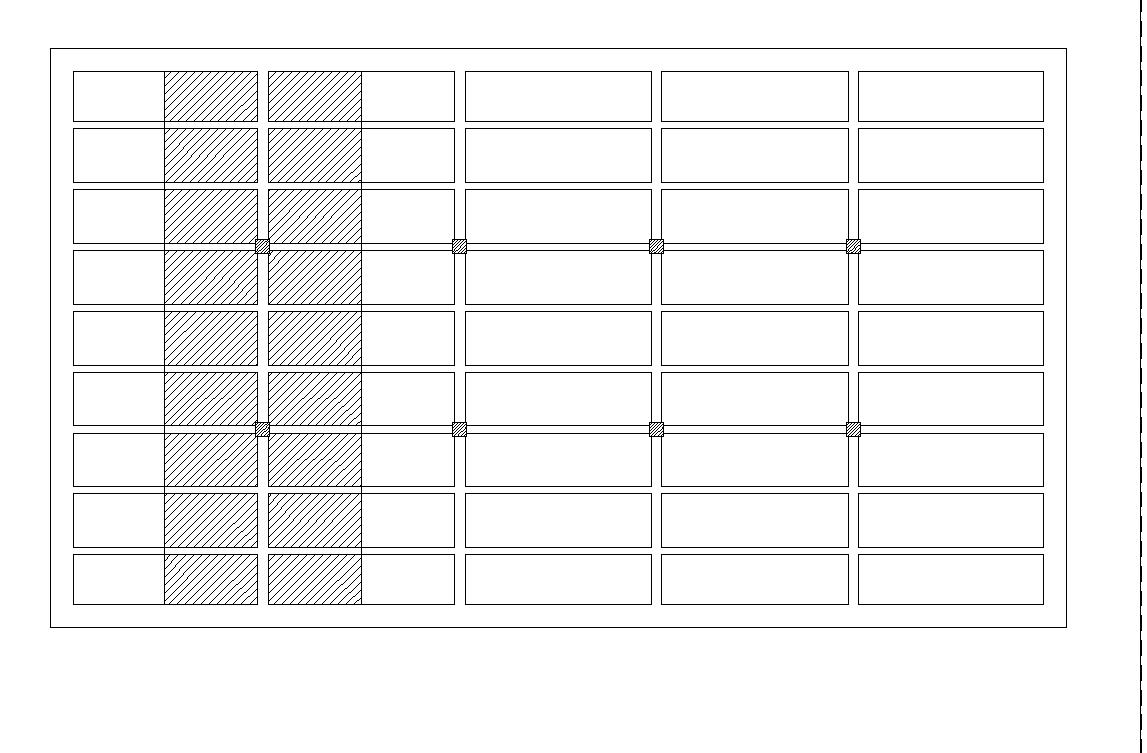
Конструктивная схема здания – неполный каркас. Строго говоря, главную балку следовало бы рассчитывать в составе рамного каркаса. Однако, для упрощения расчета ее можно рассматривать как неразрезную многопролетную балку, в которой опорами на краях являются стены, а в середине – колонны каркаса.

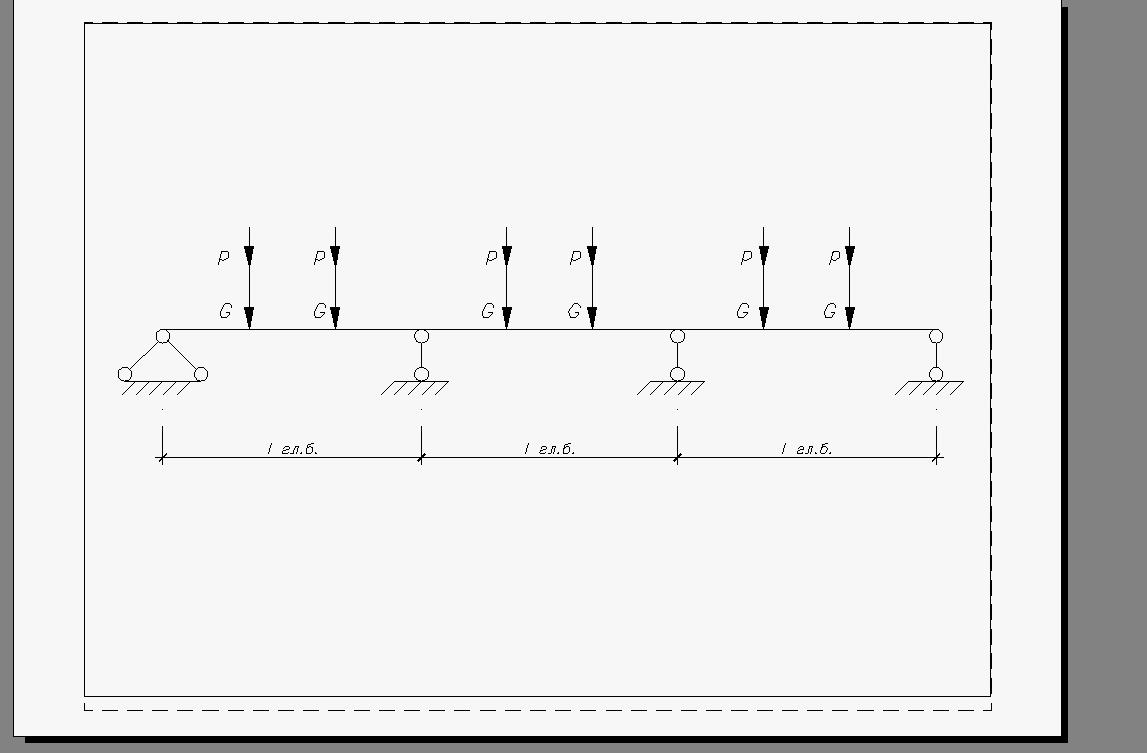
Расчетными пролетами являются размеры по осям. На главную балку нагрузка передается от второстепенных балок в виде сосредоточенных сил, за исключением собственного веса ребра главной балки.

На рисунке: G – постоянная нагрузка, действующая на главную балку, Р – временная.

G = постоянная нагрузка из таблицы на 1 м², умноженная на грузовую площадь + собственная масса ребра второстепенной балки длинной, равной ее пролету + масса ребра главной балки длинной, равной ее пролету.

Изгибающие моменты в главной балке можно определить по формуле:

Ординаты эпюры поперечных сил определяются по формуле:

где α, β, γ, δ – табличные коэффициенты, определяемые в зависимости от расположения нагрузки.

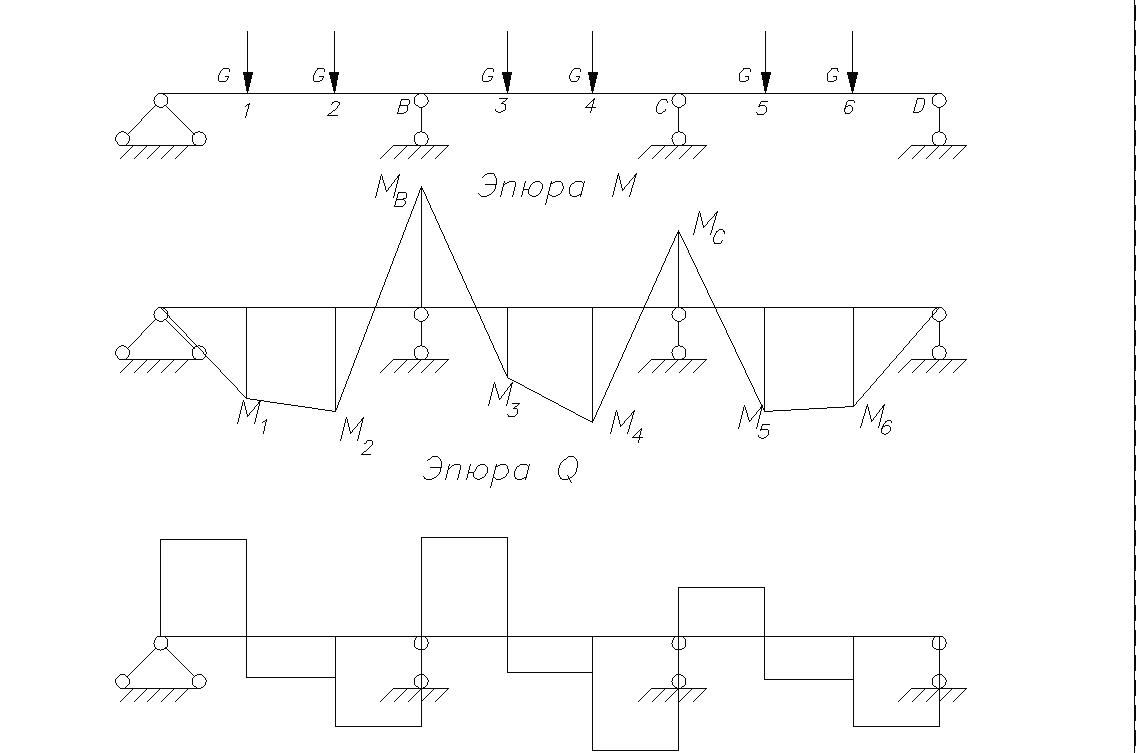
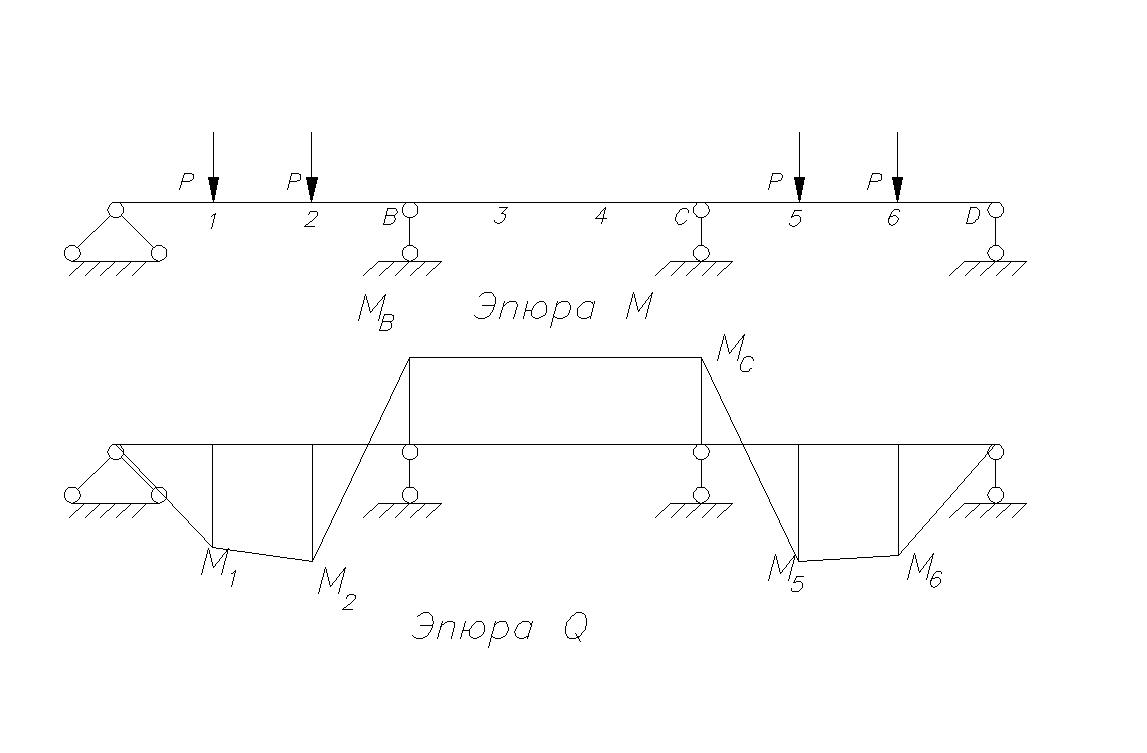
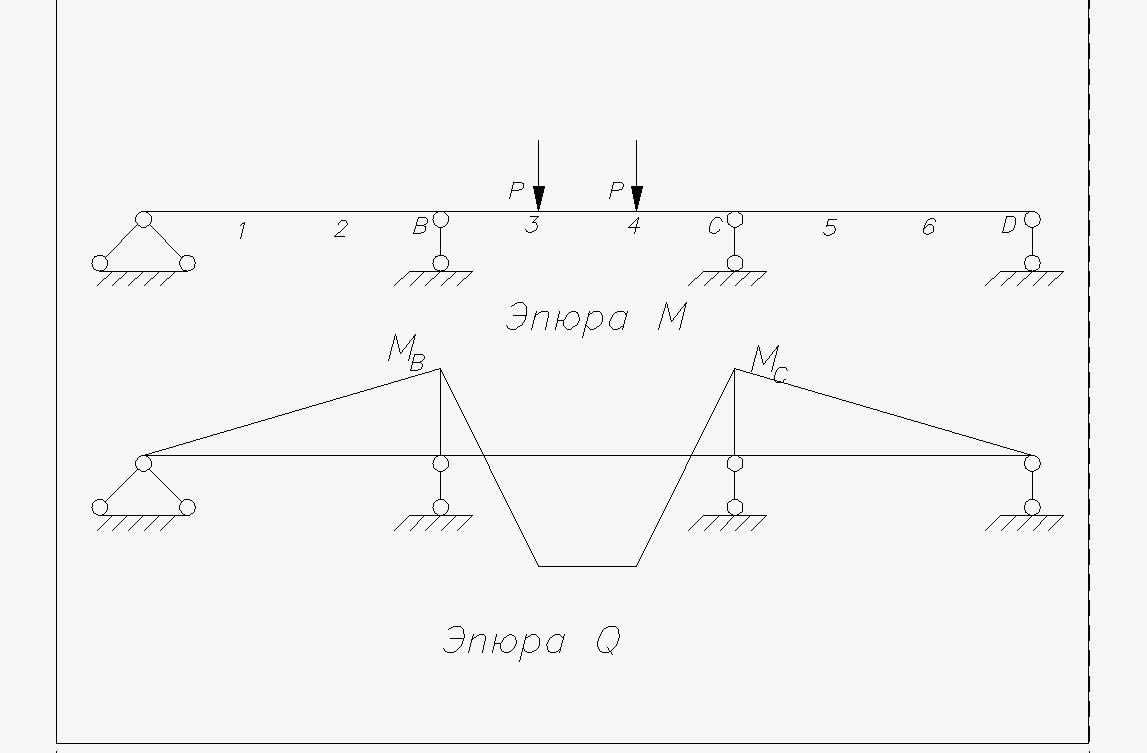
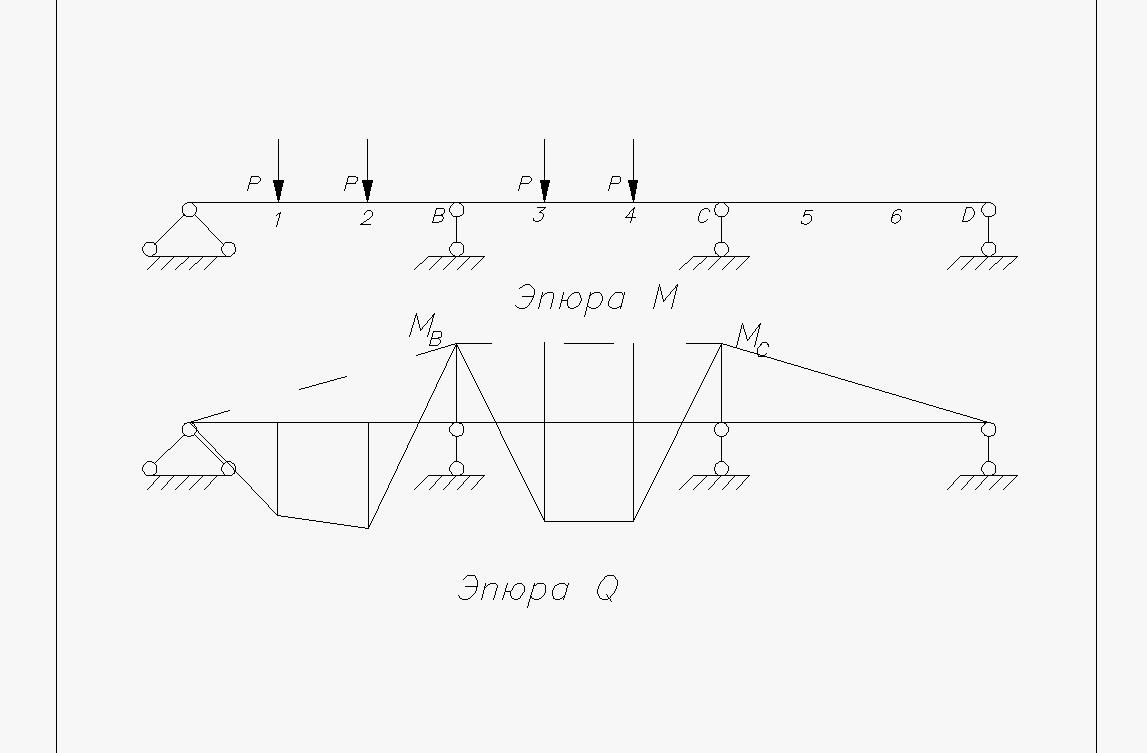
Определяем

Для определения опорных моментов соединяем точки пунктирной линией и накладываем на нее ординаты эпюры изгибающих моментов однопролетной свободно опертой балки.

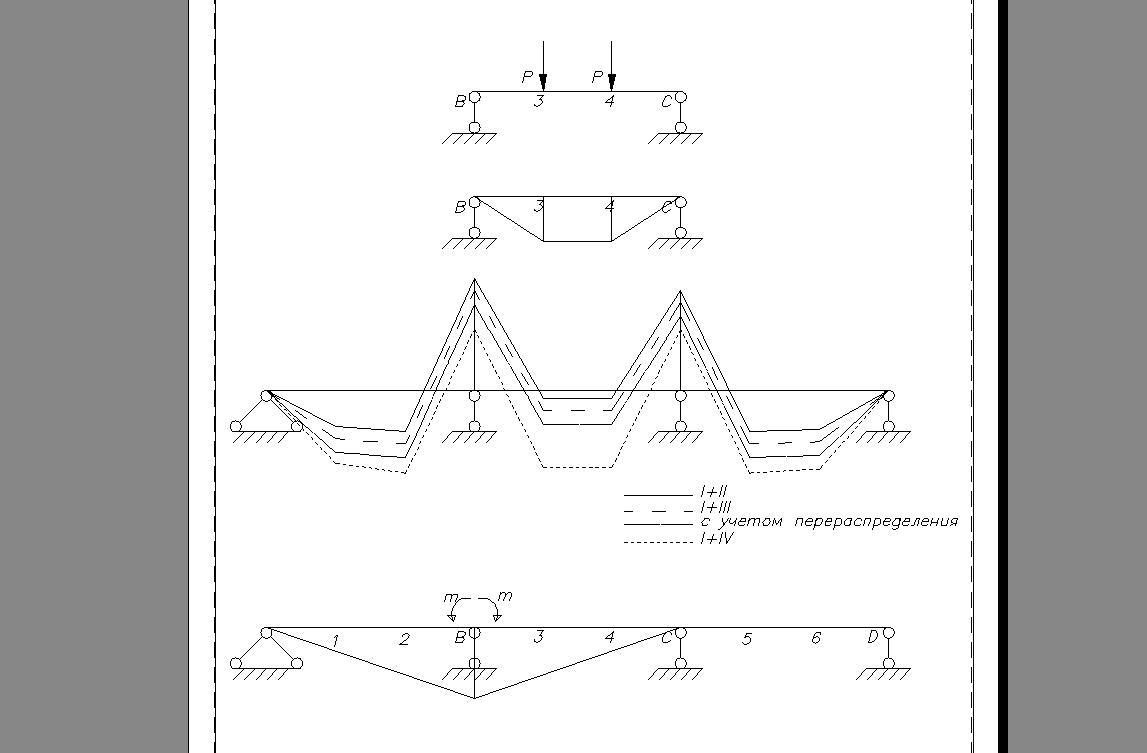
Для расчета ординат эпюры изгибающих моментов в главной балке с учетом перераспределения усилий вследствие образования пластических шарниров, полученную огибающую эпюру изгибающих моментов складываем с эпюрой изгибающих моментов от лишнего неизвестного статически определимой системы.

Ординату эпюры m можно задавать следующим образом:

1. такой величины, чтобы уменьшенный момент на опоре равнялся бы максимальному пролетному моменту, то есть пролетный и опорный момент сделать одинаковыми; для ригелей прямоугольного сечения это приведет к одинаковому их армированию на опоре и в пролете, и следовательно, к сокращению сроков строительства и облегчению соединений на опорах;

2. величиной равной 0,3 M_b

Это приведет к экономии арматуры, т.к. опорный момент уменьшится, а пролетные моменты увеличатся, но все равно будут меньше будут меньше ординат пролетных моментов при другом сочетании.

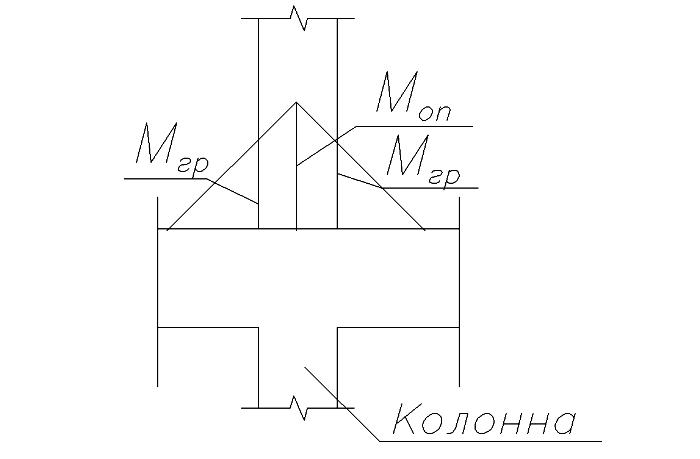
Размеры сечения главной балки, а также площадь продольной рабочей арматуры на опоре определяют по граневым изгибающим моментам, которые определяются по формуле:

где М_оп – уменьшенный опорный момент,

Q_i – минимальная ордината суммарной эпюры поперечных сил у опоры,

h_кол – размер сечения колонны в направлении длины главной балки.

Полагаем ξ≤0,35 → α_m=ξ(1-0,5ξ) → задаем b/h₀=(0,2-0,5) →

Принимаем a и b.

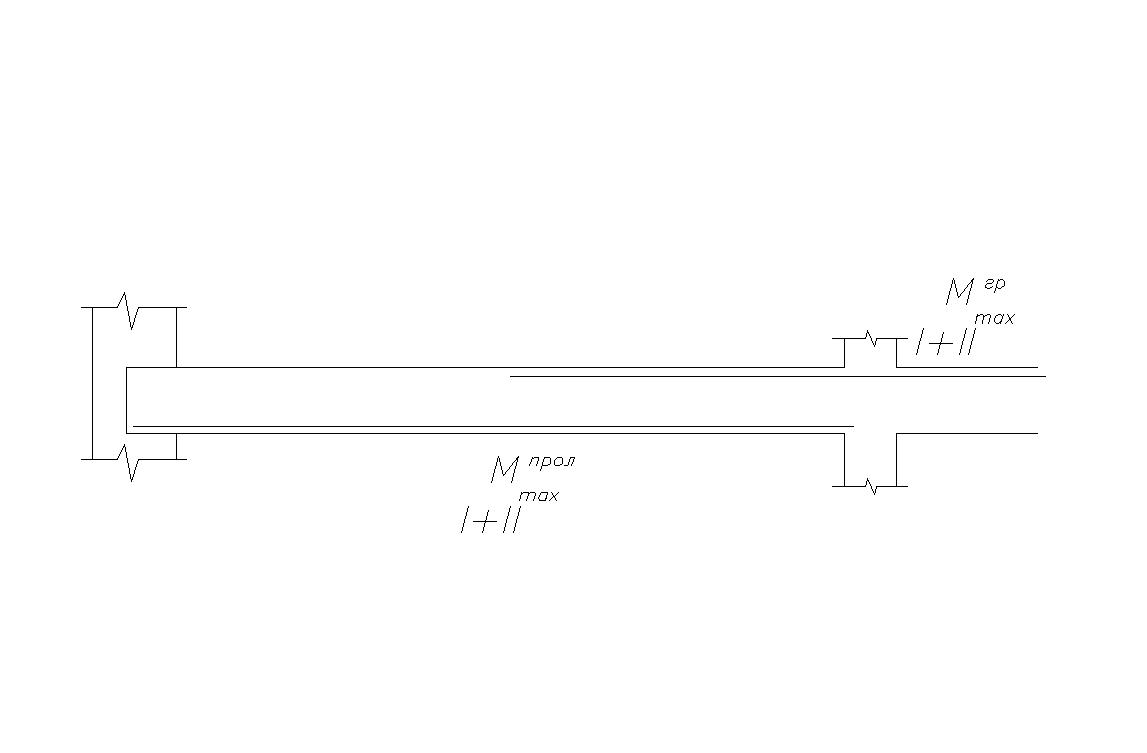
Армирование главной балки

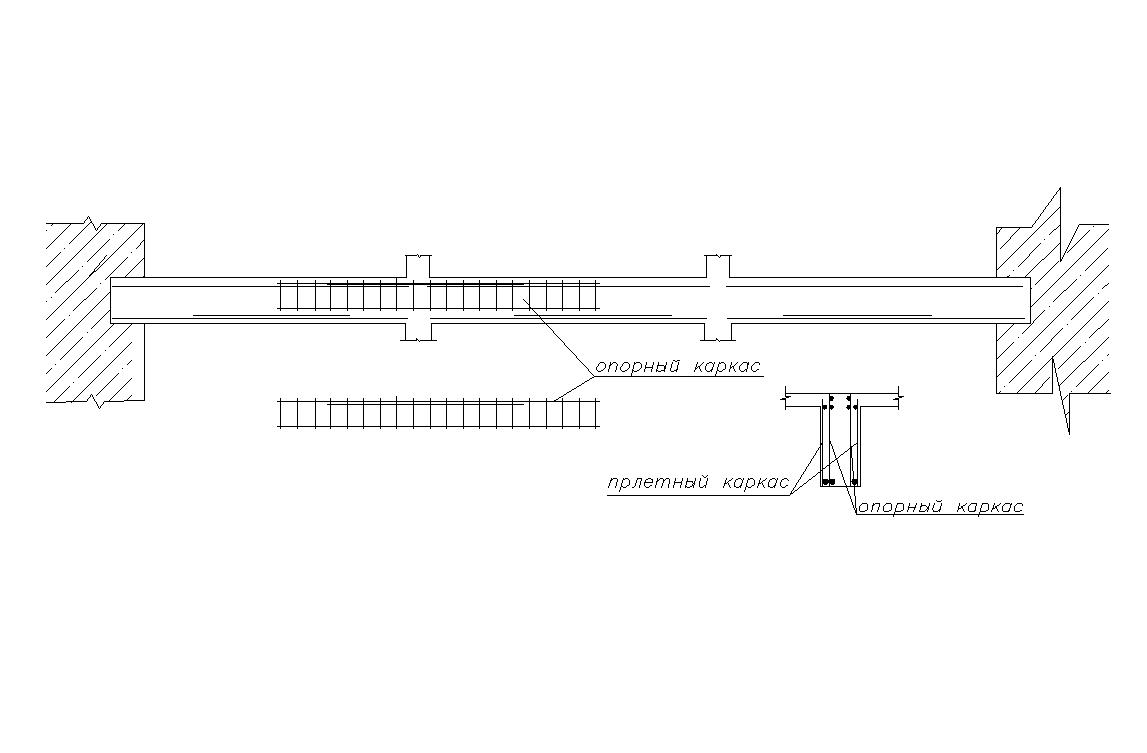
Эпюра материалов в главной балке строится аналогично эпюре материалов второстепенной балки. Главная балка на опорах армируется сварными каркасами, которые воспринимают опорный момент. Рабочая арматура на опоре может обрываться. Иногда применяют армирование на опоре со смещением каркасов.