
- •Федеральное агентство по образованию московский государственный университет технологий и управления
- •Кафедра органической, физической и коллоидной химии
- •Дистанционное
- •Коллоидная химия
- •Москва - 2008
- •Работа № 1 Определение среднего размера частиц методом седиментации в гравитационном поле
- •Работа № 2 Определение молекулярной массы полимера в растворе методом измерения вязкости
- •Работа № 3
- •Работа № 4 Адсорбция на твёрдой поверхности и молекулярная адсорбция из растворов
- •Работа № 5 Определение критической концентрации мицеллообразования коллоидного пав
- •Работа № 6 Смачивание твёрдых поверхностей
- •Работа № 7 Определение среднего размера коллоидных частиц методом турбидиметрии
- •Работа № 8 Набухание высокомолекулярных соединений
- •Краткое теоретическое введение
- •Термодинамика набухания и растворения
- •Последовательность выполнения работы
- •Обработка и оформление результатов
- •Контрольные вопросы
- •Приложение 1
- •Приложение 2
- •2.1 Построение и обработка линейного графика
- •2.2 Графическая обработка нелинейных зависимостей
- •2.3 Графическая экстраполяция
- •Лукина Ирина Георгиевна†, Зарубин Дмитрий Павлович, Козлова Лилия Вениаминовна коллоидная химия
2.2 Графическая обработка нелинейных зависимостей
Нелинейные функциональные зависимости между физическими величинами являются наименее благоприятными для их анализа графическими или вычислительными методами. Поэтому, если возможно, их преобразуют в линейные зависимости. Эта процедура называется линеаризацией. Например, рассмотренная выше зависимость приведённой вязкости от концентрации является продуктом линеаризации уравнения Хаггинса
= 0(1 + ас + bс2)
где - вязкость раствора полимера, 0 – вязкость раствора при концентрации с = 0 (то есть вязкость растворителя), а и b – коэффициенты, значения которых определялись в предыдущем разделе П2.1. Чтобы преобразовать эту зависимость в линейную делаются следующие выкладки:
![]() =
1 + ас
+ bс2
;
–
1 = ас
+ bс2
;
=
1 + ас
+ bс2
;
–
1 = ас
+ bс2
;
![]() =
ас
+ bс2
;
=
ас
+ bс2
;
![]() =
а
+ bс
=
а
+ bс
Последнее уравнение в этой серии является линейным, вида
y = a + bx, где х = с и у = r = .
К сожалению, процедура линеаризации возможна далеко не всегда. Существует много зависимостей y = (x), точный вид функции которых не известен и которые не могут быть линеаризованы по этой причине. Обычная задача, с которой приходится сталкиваться в этом случае, – нахождение производной (dy/dx) при некотором значении х графическим методом.
Для решения этой задачи следует выбрать по возможности большой размер графика (например целый лист формата А4) и использовать те же стадии построения, которые описаны в приложении 2.1. вплоть до стадии построения диаграммы рассеяния. На следующей стадии, построение графика "по точкам" осуществляется, в общем, по тому же принципу минимального отклонения точек от графика функции. Особенность этой стадии заключается в том, что она является менее определённой и допускающей больше произвола, чем в случае линейного графика. Всё же, как правило, эта стадия не является полностью произвольной, потому что мы обычно знаем кое-что о функции, с которой имеем дело. Мы можем знать, например, является она убывающей или возрастающей, имеет ли экстремум (максимум или минимум), асимптоту, точки перегиба (точки, в которых чередуется выпуклость и вогнутость кривой), или какие-то частные точки (например, значение у при х = 0). Такие знания необходимо использовать для сокращения неопределённости и произвольности в построении графика.
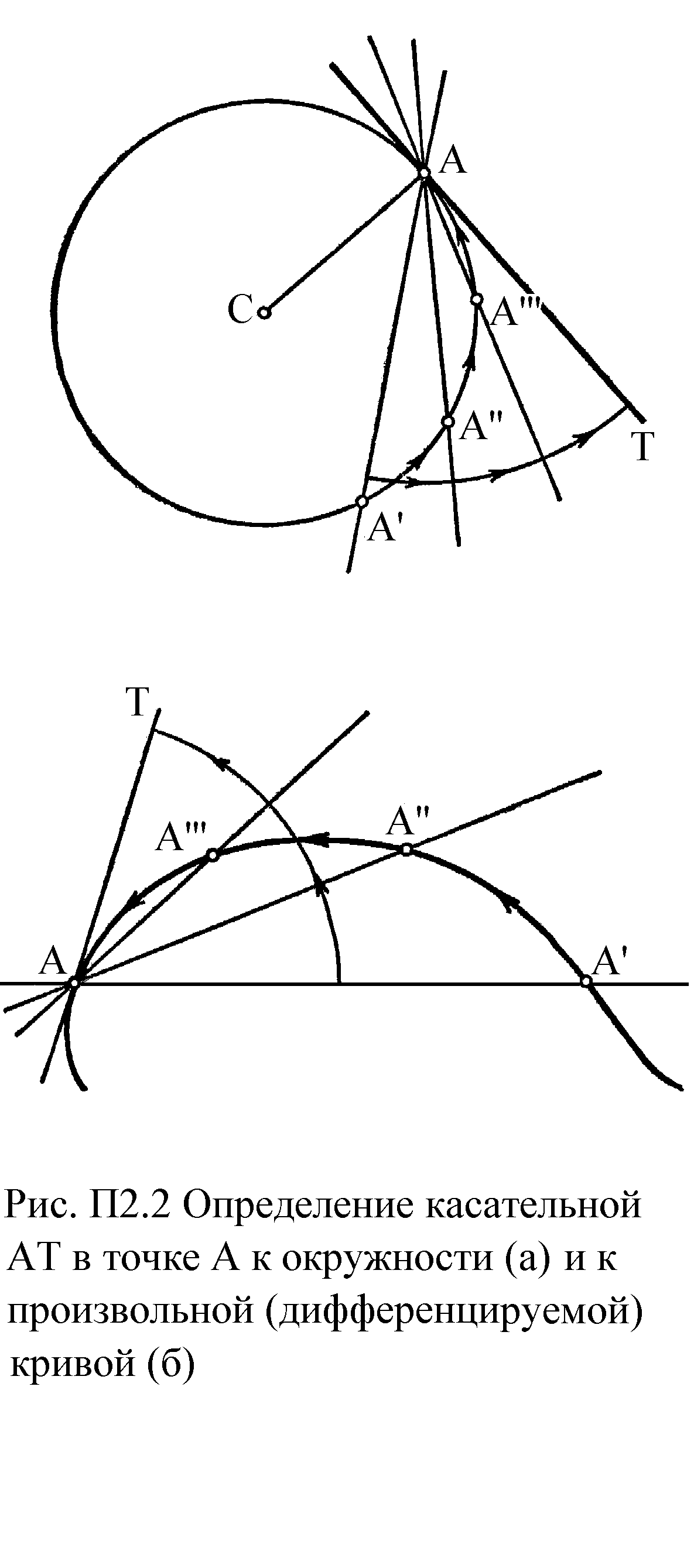
На следующей стадии необходимо найти касательную к построенной кривой при заданном х. Графическое определение касательной – это прямая, представляющая предельное положение секущей, при котором длина отсекаемой дуги равна нулю. Рисунок П2.2 иллюстрирует это определение на примере окружности (рис. а) и произвольной (дифференцируемой) кривой (рис. б). Пусть дана точка А на окружности (рис. а). Выберем любую другую точку на окружности А' и соединим её с А секущей АА'. Пусть точка А' движется по окружности в направлении уменьшения длины отсекаемой дуги через последовательные положения A'', А''', … Очевидно, что в пределе секущая займёт такое положение АТ, при котором она будет иметь только одну общую точку с окружностью, именно точку А. В таком положении она называется касательной.
 Это
определение можно использовать
практически для нахождения касательной
в точке А. Для этого следует положить
линейку так чтобы она проходила через
точку А и произвольную точку А', и
поворачивать её вокруг А до положения
АТ. (Чтобы линейка не смещалась от точки
А при движении, можно воткнуть булавку
рядом с этой точкой и слегка опираться
на неё краем линейки).
Это
определение можно использовать
практически для нахождения касательной
в точке А. Для этого следует положить
линейку так чтобы она проходила через
точку А и произвольную точку А', и
поворачивать её вокруг А до положения
АТ. (Чтобы линейка не смещалась от точки
А при движении, можно воткнуть булавку
рядом с этой точкой и слегка опираться
на неё краем линейки).
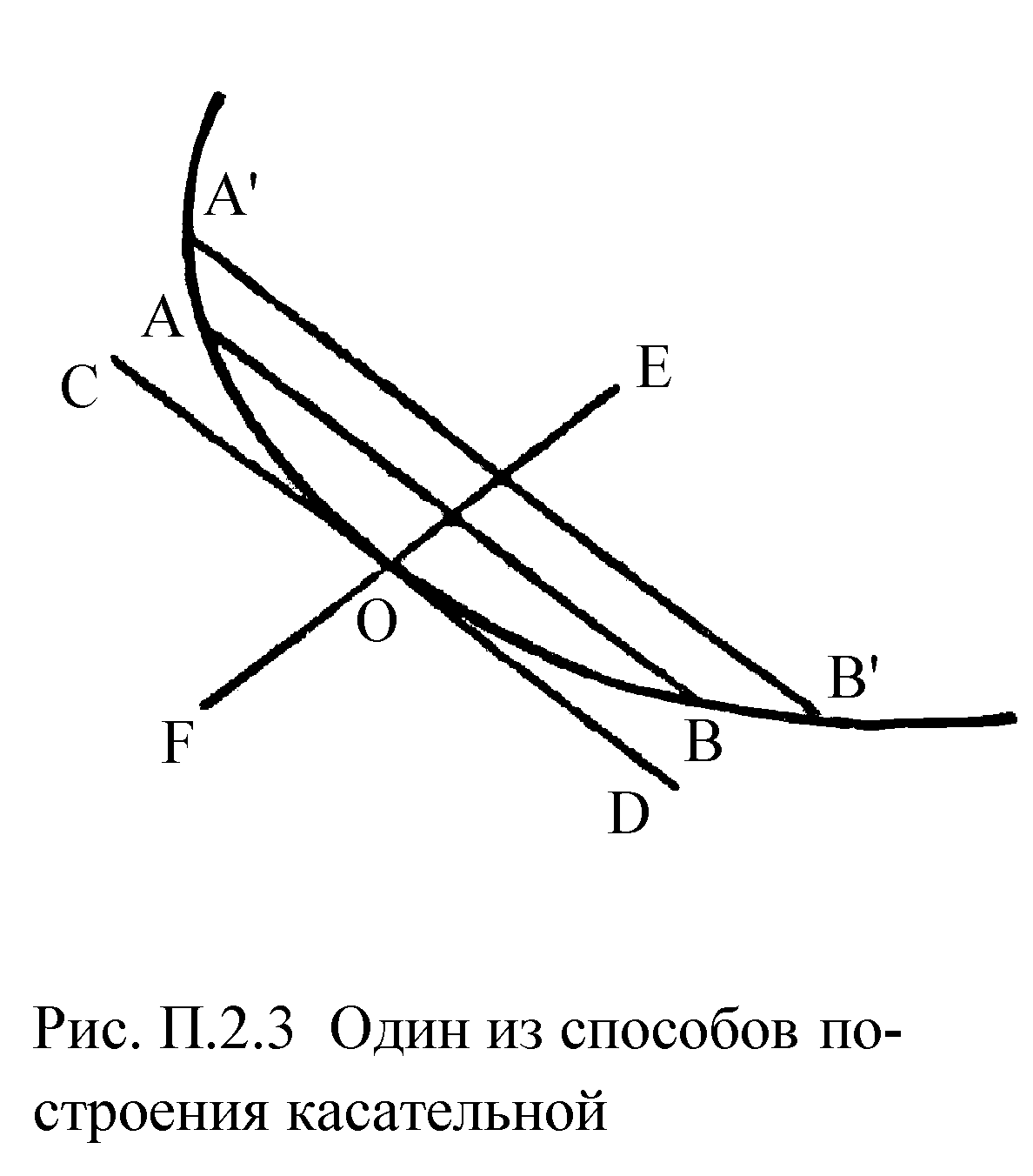 Другой
метод построения касательной показан
на рис. П2.3. На выбранном отрезке кривой
проводят две параллельные хорды АВ и
A'B'. Делят их пополам и через полученные
середины проводят прямую EF, пересекающую
кривую в точке О. Прямая CD, проведённая
через найденную точку О параллельно
хордам АВ и A'B', является касательной к
кривой в точке О. Следует обратить
внимание, что в этом методе мы не задаёмся
заранее точкой О, через которую должна
быть проведена касательная, а находим
её путём построений. Предварительно мы
задаёмся только дугой АОВ, в пределах
которой эта точка оказывается. Мы делаем
это неявно проведением хорды АВ.
Другой
метод построения касательной показан
на рис. П2.3. На выбранном отрезке кривой
проводят две параллельные хорды АВ и
A'B'. Делят их пополам и через полученные
середины проводят прямую EF, пересекающую
кривую в точке О. Прямая CD, проведённая
через найденную точку О параллельно
хордам АВ и A'B', является касательной к
кривой в точке О. Следует обратить
внимание, что в этом методе мы не задаёмся
заранее точкой О, через которую должна
быть проведена касательная, а находим
её путём построений. Предварительно мы
задаёмся только дугой АОВ, в пределах
которой эта точка оказывается. Мы делаем
это неявно проведением хорды АВ.
Описанные два метода построения эффективны только в тех случаях, когда точка касания находится на участке кривой, на котором кривизна является приблизительно постоянной, или, проще говоря, когда этот участок похож по своей форме на дугу окружности.
Наиболее универсальным и надёжным является метод прямоугольного зеркала. Такое зеркальце ставят ребром поперёк кривой так, чтобы его край с отражающей стороны проходил через заданную точку касания. Затем его поворачивают вокруг этой точки до положения, при котором отражение в зеркале выглядит продолжением (без излома) отрезка кривой, расположенного перед зеркалом. Когда такое положение найдено, отмечают след зеркала, проведя прямую по его краю. Затем зеркало отнимают и проводят прямую, проходящую через заданную точку перпендикулярно следу зеркала. Эта последняя прямая является касательной.
Производная функции у = (х) в точке касания равна по определению коэффициенту наклона касательной. Этот коэффициент находят так же, как угловой коэффициент линейного графика (см. выше приложение 2.1). То есть, чтобы найти его графическим методом, нужно отвлечься от нелинейного графика у = (х) и от точки касания на нём, и рассматривать построенную касательную как отдельный линейный график.
