Функция zтест Служит для проверки гипотезы о числовом значении средней нормального распределения при известной дисперсии.

Синтаксис:

ZТЕСТ (массив; х; сигма)

Массив: массив данных, с которыми сравнивается х;

Х: проверяемое значение;

Сигма: известное стандартное отклонение генеральной совокупности. Если этот аргумент опущен, то используется оценка генерального стандартного отклонения по выборке.

Замечания:

· Если массив пуст, то функция ZТЕСТ помещает значение ошибки #Н/Д.

Математико-статистическая интерпретация:

Рассматривается случайная величина X=N(a,), причем числовое значение математического ожидания а не известно, а числовое значение дисперсии ² известно. Выдвигается гипотеза H₀ о том, что среднее равно числу а₀, то есть H₀: а = a₀

В качестве критерия проверки гипотезы берется величина

,

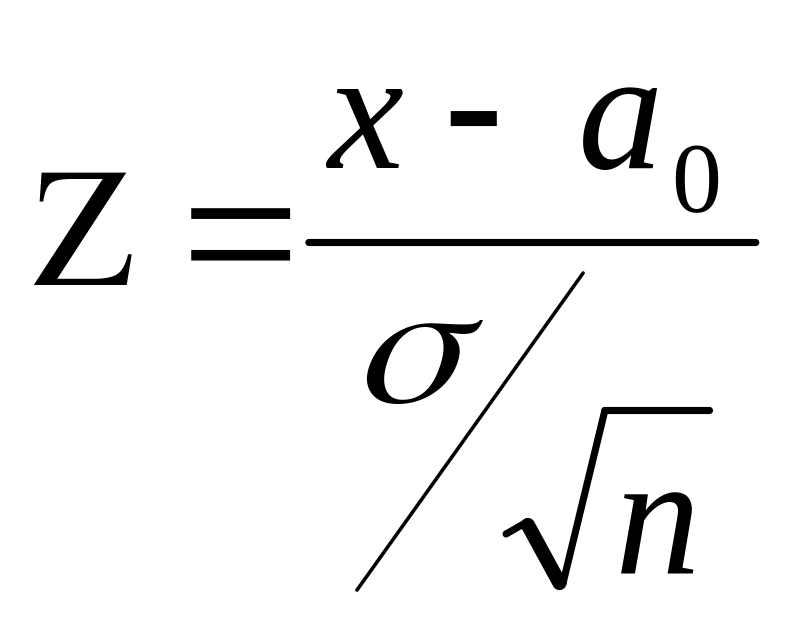которая при выполнении гипотезы подчиняется нормальному закону распределения с нулевым математическим ожиданием и единичной дисперсией.

Режимы работы «Двухвыборочный t-тест с одинаковыми дисперсиями» и «Двухвыборочный t-тест с различными дисперсиями» служат для проверки гипотез о различии между средними двух нормальных распределений соответственно с неизвестными, но равными дисперсиями и с неизвестными дисперсиями, равенство которых не предполагается.

В диалоговых окнах режимов задаются параметры, аналогичные параметрам, задаваемым в диалоговом окне «Двухвыборочный - тест для средних», только отсутствуют поля Дисперсия переменной 1 и Дисперсия переменной 2.

Замечание. Для расчетов в режиме «Двухвыборочный t- тест c одинаковыми дисперсиями» и «Двухвыборочный t- тест c различными дисперсиями» используются ряд статистических функций (СРЗНАЧ (в ячейках В39, С39), СЧЕТ (в ячейках В41, С41), ДИСП (в ячейках В40,С40), СТЬЮДРАСПОБР (в ячейке В45)). Функция ТТЕСТ является родственной по своей сущности с описанными выше режимами.

Функция ТТЕСТ

Возвращает вероятность, соответствующую критерию Стьюдента. Функция ТТЕСТ используется, чтобы определить, насколько вероятно, что две выборки взяты из генеральных совокупностей, которые имеют одно и то же среднее.

Синтаксис

ТТЕСТ(массив1;массив2;хвосты;тип)

Массив1: первое множество данных.

Массив2: второе множество данных.

Хвосты: число хвостов распределения. Если хвосты = 1, то функция ТТЕСТ использует одностороннее распределение. Если хвосты = 2, то функция ТТЕСТ использует двустороннее распределение.

Тип: вид исполняемого t-теста.

Тип Выполняемый тест

1 Парный

2. Двухвыборочный с равными дисперсиями

3. Двухвыборочный с неравными дисперсиями

Замечания:

· Если массив1 и массив2 имеют различное число точек данных, а тип = 1 (парный), то функция ТТЕСТ возвращает значение ошибки #Н/Д.

· Аргументы хвосты и тип усекаются до целых.

· Если хвосты или тип не является числом, то функция ТТЕСТ возвращает значение ошибки #ЗНАЧ!.

· Если хвосты имеет значение, отличное от 1 и 2, то функция ТТЕСТ возвращает значение ошибки #ЧИСЛО!

В Excel имеется возможность для проверки гипотезы о равенстве дисперсий двух нормальных распределений. Режим «Двухвыборочный F- тест для дисперсий» позволяет осуществить эту проверку быстро и качественно. В диалоговом окне данного режима задаются параметры, аналогичные параметрам, задаваемым в диалоговом окне «Двухвыборочный - тест для средних», только отсутствуют поля Дисперсия переменной 1, Дисперсия переменной 2 и Гипотетическая разность.

Замечание. Для расчетов в режиме «Двухвыборочный F- тест для дисперсий» используются ряд статистических функций. Функция ФТЕСТ является родственной по своей сущности с описанным выше режимом.

Функция ФТЕСТ

Возвращает результат F-теста. F-тест возвращает одностороннюю вероятность того, что дисперсии аргументов массив1 и массив2 различаются несущественно. Эта функция используется для того, чтобы определить, имеют ли две выборки различные дисперсии. Например, если даны результаты тестирования для частных и общественных школ, то можно определить, имеют ли эти школы различные уровни разнородности учащихся.

Синтаксис:

ФТЕСТ (массив 1;массив 2)

Массив 1 - это первый массив или интервал данных.

Массив 2 - это второй массив или интервал данных.

Замечания:

· Аргументы должны быть числами или именами, массивами или ссылками, содержащими числа.

· Если аргумент, который является массивом или ссылкой, содержит тексты, логические значения или пустые ячейки, то такие значения игнорируются; однако, ячейки с нулевыми значениями учитываются.

· Если количество точек данных в аргументе массив 1 или массив 2 меньше 2, или если дисперсия аргумента массив1 или массив 2 равна нулю, то функция ФТЕСТ возвращает значение ошибки #ДЕЛ/0!

Примечание. 1. Функция ФТЕСТ рассчитывает двустороннее Р-значение F-теста, поэтому в данном случае полученное значение необходимо поделить на 2.

2. Если s_х²  s_y², то Р-значение рассчитывается с помощью функции FРАСПР.

Функция FРАСПР

Рассчитывает F – распределение Фишера.

Синтаксис:

FРАСПР (х; степени _свободы1; степени _свободы 2)

Х – значение, для которого вычисляется F – распределение;

степени _свободы1: первое число степеней свободы k;

степени _свободы2: второе число степеней свободы l.

Замечания:

· Если какой-либо из аргументов не является числом, то функция FРАСП возвращает значение ошибки #ЗНАЧ!;

· Если аргумент х < 0, то функция FРАСП возвращает значение ошибки #ЧИСЛО!;

· Если степени_свободы не целое, то оно усекается;

· Если степени_свободы < 1 или степени_свободы  10¹⁰, функция FРАСП возвращает значение ошибки #ЧИСЛО!.

На практике чаще применяется функция FРАСПОПР, рассчитывающая значение F – критерия для заданного уровня значимости  и числа степеней свободы k и l.