Лабораторная работа № 8 Тема: “Статистические сравнения в режимах надстройки «Пакет анализа»”

1. Краткие сведения из математической статистики

Проверка гипотез о равенстве двух центров распределения имеет важное практическое значение. Иногда оказывается, что средний результат одной серии экспериментов заметно отличается от среднего результата другой серии. При этом возникает вопрос: можно ли объяснить обнаруженное расхождение средних случайными ошибками эксперимента или оно вызвано какими-либо незамеченными или даже неизвестными закономерностями? В промышленности задача сравнения средних возникает при выборочном контроле качества изделий, изготовленных на разных установках или при разных технологических режимах; в экономике, например, при проверки доли новых видов доходов от предпринимательской деятельности по результатам выборочных обследований в двух областях, традиционных для рыночной экономики; в педагогике для измерения изучаемого свойства после применения новых технологий обучения.

Параметрические критерии обладают более сильной разрешающей способностью, большей мощностью по сравнению с критериями непараметрическими, поэтому во всех случаях, когда исследуемая совокупность распределяется по нормальному закону или не очень сильно отклоняется от него, следует отдавать предпочтение критериям параметрическим.

Для обработки статистических данных в Microsoft Excel существует надстройка Пакет анализа, изучение которой было начато в 6 лабораторной работе. Режимы работы, используемые для проверки статистических гипотез, будут рассмотрены в настоящей работе.

1. Гипотеза о равенстве средних при известных дисперсиях

Изучаются две случайные величины X и Y, числовые значения дисперсий ²_x и ²_y которой известны, числовые значения средних а_x и a_y неизвестны. При сформулированных условиях требуется проверить гипотезу о равенстве математических ожиданий случайных величин X и Y, то есть гипотезу H₀: а_x = a_y . В математической статистике доказывается, что если данная гипотеза выполняется, то величина

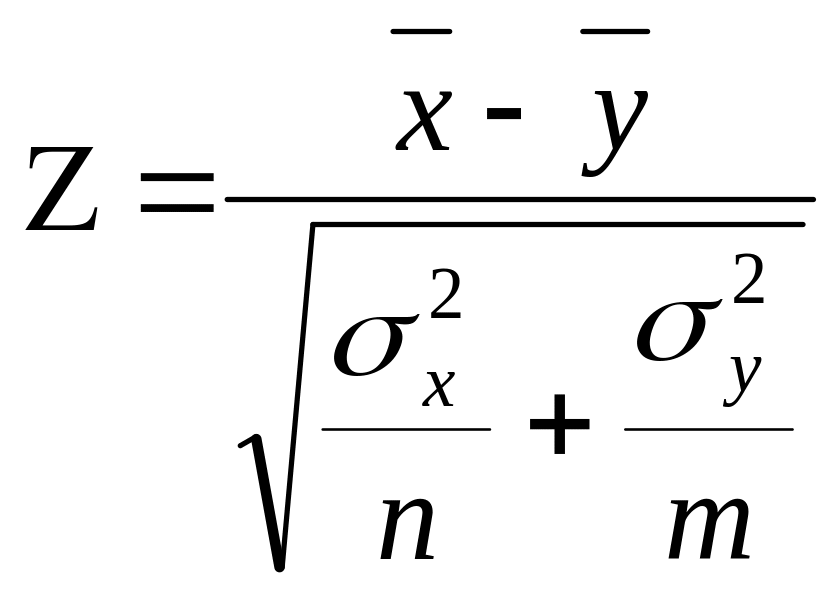
имеет нормальный закон распределения с нулевым математическим ожиданием и единичной дисперсией. Величину  используют в качестве критерия при проверке гипотезы H₀: а_x = a_y .

Критическая область строиться в зависимости от вида конкурирующей гипотезы. Если конкурирующая гипотеза H₁: a_xa_y, то строят двустороннюю критическую область, и Z_кр находят из условия Если конкурирующая гипотеза H₁: a_xa_y, то строят правостороннюю критическую область, и Z_кр находят из условия Для гипотезы H₁: a_xa_y строят левостороннюю критическую область, и аналогично находят Z_кр.

2. Гипотеза о равенстве средних при неизвестных дисперсиях

Критерий проверки такой гипотезы довольно прост, если известно, что неизвестные дисперсии ²_x и ²_y равны. Величина

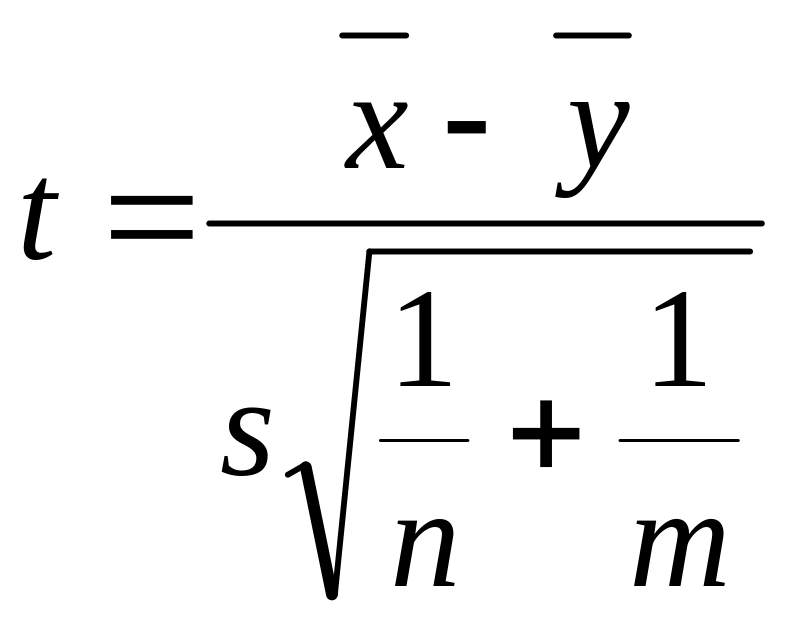
имеет распределение Стьюдента с k=n+m-2 степенями свободы и ее используют для проверки гипотезы H₀: а_x = a_y .

Если же заранее не известно, что ²_{x =} ²_y, то, прежде чем проверять гипотезу H₀: а_x = a_y, проверяют гипотезу H₀:²_x ²_y. И в случае приемлемости H₀ приступают с некоторой осторожностью, к проверке гипотезы H₀: а_x = a_y.