
- •1. Свойство. 2. Свойство. 3. Свойство. .
- •6.1.4.4.Скалярное произведение равно произведению длины одного из векторов на проекцию другого на направление первого: .
- •6.1.4.5.Распределительный закон. .
- •6.4.2. 5. Смешанное произведение изменит знак при перестановке двух векторов.
- •8.2.3.2. Гиперболический цилиндр:
- •8.2.3.3. Параболический цилиндр:
8.2.3.2. Гиперболический цилиндр:
Осью цилиндра служит ось Одна из направляющих цилиндра –гипербола, расположенная в плоскости .
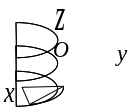
8.2.3.3. Параболический цилиндр:
Осью цилиндра служит ось Одна из направляющих цилиндра –парабола, расположенная в плоскости .
Трехосный эллипсоид.

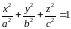
Эллипсоиды вращения.
Если
эллипс
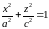 ,
расположенный в плоскости
,
вращать вокруг оси
,
то получившаяся поверхность
,
расположенный в плоскости
,
вращать вокруг оси
,
то получившаяся поверхность
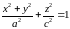 является эллипсоидом (эллипсоид
вращения).
является эллипсоидом (эллипсоид
вращения).
Этот же
эллипсоид получится, если эллипс
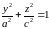 ,
расположенный в плоскости
,
расположенный в плоскости
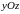 ,
вращать вокруг оси
.
,
вращать вокруг оси
.
Поверхности
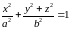 и
и
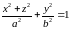 также
являются эллипсоидами вращения.
также
являются эллипсоидами вращения.
Однополостный гиперболоид.

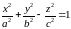
Однополостные гиперболоиды вращения.
Если
гиперболу
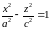 ,
расположенную в плоскости
,
вращать вокруг оси
,
то получившаяся поверхность
,
расположенную в плоскости
,
вращать вокруг оси
,
то получившаяся поверхность
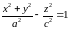 является однополостным гиперболоидом
(однополостным гиперболоид вращения).
является однополостным гиперболоидом
(однополостным гиперболоид вращения).
Такой же
гиперболоид получится, если гиперболу
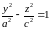 ,
расположенную в плоскости
,
вращать вокруг оси
,
расположенную в плоскости
,
вращать вокруг оси
Поверхности
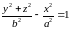 и
и
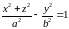 также
являются гиперболоидами вращения.
также
являются гиперболоидами вращения.
Двуполостный гиперболоид.
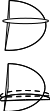
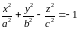
Двуполостные гиперболоиды вращения.
Если
гиперболу
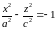 ,
расположенную в плоскости
,
вращать вокруг оси
,
то получившаяся поверхность
,
расположенную в плоскости
,
вращать вокруг оси
,
то получившаяся поверхность
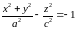 является двуполостным гиперболоидом
(двуполостный гиперболоид вращения).
является двуполостным гиперболоидом
(двуполостный гиперболоид вращения).
Этот же
гиперболоид получится, если гиперболу
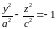 ,
расположенную в плоскости
,
вращать вокруг оси
.
,
расположенную в плоскости
,
вращать вокруг оси
.
Поверхности
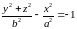 и
и
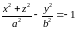 также
являются двуполостными гиперболоидами
вращения.
также
являются двуполостными гиперболоидами
вращения.
К онус
второго порядка.
онус
второго порядка.
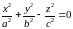
Круговой конус.
Конус
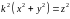 ,
который получается вращением прямой
,
который получается вращением прямой
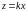 вокруг оси
вокруг оси
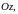 называется круговым конусом.
Сечение этого конуса плоскостью,
перпендикулярной оси конуса, является
окружностью
называется круговым конусом.
Сечение этого конуса плоскостью,
перпендикулярной оси конуса, является
окружностью
Эллиптический параболоид.

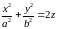
Гиперболический параболоид.

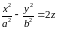
Общее
уравнение 2-го порядка относительно
Общим
уравнением 2-го порядка относительно
называют
уравнение вида:
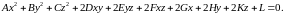
10) Определители и матрицы.
Определение матрицы.
Матрицей называется
прямоугольная таблица элементов
(напр.чисел), расположенных в
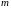 строках
и
строках
и
 столбцах.
столбцах.
Частные виды матриц: матрица из одного элемента, матрица-столбец, матрица-строка, квадратная матрица, нулевая матрица, диагональная матрица, единичная матрица, ступенчатая матрица.
Матрица
из одного элемента:
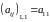 .
.
Матрица
из одной строки:
 .
.
Матрица
из одного столбца:
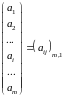 .
Квадратная матрица
.
Квадратная матрица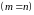 :
:
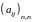 .
.
Нулевая
матрица все элементы равны нулю:
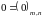 .
.
Единичная матрица- квадратная матрица, у которой диагональные элементы равны 1, а остальные элементы равны 0.
 ,
где
,
где
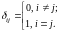
Диагональная матрица- квадратная матрица, у которой диагональные (или некоторые из них) элементы отличны от нуля, а остальные элементы равны 0.
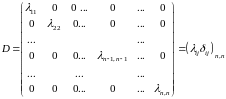 .
.
Ступенчатая
матрица – матрица, у которой в
 строках
строках
 элементы
над диагональю отличны от нуля (или
некоторые из них), а остальные строки
состоят из нулей:
элементы
над диагональю отличны от нуля (или
некоторые из них), а остальные строки
состоят из нулей:
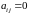 при
при
 .
.
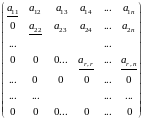
Определители. Определители 3-го порядка.
Определителем
квадратной матрицы
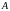 называется число, которое ставится в
соответствие квадратной матрице по
определенному правилу.
Определитель
третьего порядка (см. Лекция 1.)
ставится в соответствие квадратной
матрице
называется число, которое ставится в
соответствие квадратной матрице по
определенному правилу.
Определитель
третьего порядка (см. Лекция 1.)
ставится в соответствие квадратной
матрице
Вычисление определителя 3-го порядка.
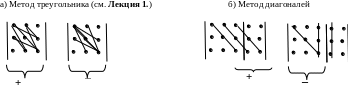
Свойства определителей.
10.3.2.1. Величина определителя не изменится, если в нем каждую строку заменить на столбец с тем же номером. 10.3.2.2.При перестановке параллельных рядов абсолютная величина определителя не изменится. Знак при каждой перестановке меняется на противоположный. 10.3.2.3.Если у определителя имеется два одинаковых ряда (две строки или два столбца), то определитель равен 0. 10.3.2.4. Общий множитель какого-либо ряда определителя можно вынести за знак определителя. (Если элементы какого-либо ряда определителя умножить на одно и то же число, то значение определителя умножится на это число.) 10.3.2.5.Если элементы какого-либо ряда определителя равны нулю, то определитель равен нулю. 10.3.2.6. Если у определителя имеется два пропорциональных ряда (две строки или два столбца), то определитель равен 0. 10.3.2.7. Если каждый элемент какого-либо ряда определителя представляет сумму двух слагаемых, то он может быть представлен в виде суммы двух определителей. 10.3.2.8. Если к элементам какого-либо ряда определителя прибавить соответственно элементы параллельного ряда, умноженные на одно и то же число, то величина определителя не изменится.
Миноры и алгебраические дополнения.
Минором
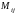 элемента
элемента
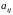 определителя называется определитель,
получаемый вычеркиванием строки и
столбца, на пересечении которых расположен
элемент
.
Алгебраическим
дополнением
определителя называется определитель,
получаемый вычеркиванием строки и
столбца, на пересечении которых расположен
элемент
.
Алгебраическим
дополнением
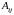 элемента
определителя называется число
элемента
определителя называется число
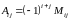 .
.
Величина определителя любого порядка (разложение определителя по элементам ряда).
Определитель
равен сумме произведений элементов
какого-нибудь ряда на их алгебраические
дополнения.
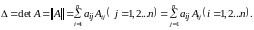
Особенные, неособенные матрицы.
Квадратная матрица, определитель которой равен нулю называется особенной (вырожденной). Квадратная матрица, определитель которой не равен нулю называется неособенной (невырожденной).
Линейные операции с матрицами: умножение матрицы на число и сложение матриц.
Произведением
матрицы
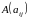 на
число
называется матрица
на
число
называется матрица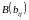 ,
элементы которой равны
,
элементы которой равны
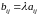 для
для
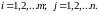
Суммой
матриц
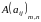 и
и
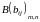 называется матрица
называется матрица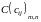 ,
элементы которой равны
,
элементы которой равны
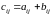 для
(Матрицы
складываются поэлементарно.)
для
(Матрицы
складываются поэлементарно.)
Нулевая матрица.
Нулевой
матрицей
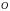 называется
матрица, все элементы которой равны 0.
называется
матрица, все элементы которой равны 0.
Свойства линейных операций с матрицами.
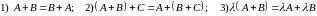
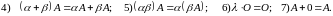
8) Для
любых матриц
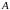 и
и
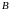 одинакового размера существует
единственная матрица
одинакового размера существует
единственная матрица
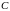 такая,
что
такая,
что
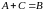 .
Матрица
называется
разностью матриц
и
:
.
Матрица
называется
разностью матриц
и
: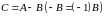 .
.
Транспонирование матриц.
Пусть
имеется матрица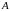 ,
содержащая
,
содержащая
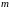 строк
и
строк
и
 столбцов.
Матрица
столбцов.
Матрица
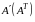 строками
которой служат столбцы матрицы
называется матрицей, транспонированной
матрице
.
строками
которой служат столбцы матрицы
называется матрицей, транспонированной
матрице
.
Свойства операции транспонирования.
1.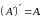 2.
2.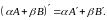 3.
3.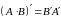 .
.
4.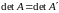 (
Определитель матрицы
(
Определитель матрицы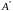 ,
транспонированной матрице
,
равен определителю матрицы
).
,
транспонированной матрице
,
равен определителю матрицы
).
Симметрическая матрица.
Если матрица совпадает с матрицей , то матрица называется симметричной матрицей.
Умножение матриц.
Произведение
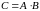 матрицы
на матрицу
определено
только в случае, когда число
столбцов первой матрицы равно числу
строк второй.
матрицы
на матрицу
определено
только в случае, когда число
столбцов первой матрицы равно числу
строк второй.
Определение.
Произведением
матрицы
на матрицу
называется
матрица, каждый элемент
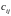 которой определяется равенством:
которой определяется равенством: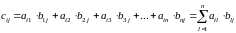
 Если
матрица
Если
матрица
 имеет
имеет строк
и
строк
и
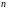 столбцов,
а матрица
столбцов,
а матрица
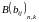 -
строк
и
-
строк
и
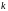 столбцов,
то матрица
столбцов,
то матрица
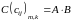 имеет
строк и
столбцов.
имеет
строк и
столбцов.
Свойства умножения матриц.
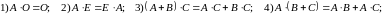
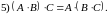 6)
Если
и
6)
Если
и
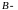 квадратные
матрицы одного порядка, то
квадратные
матрицы одного порядка, то
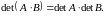
Перестановочные матрицы.
Квадратные матрицы
одинакового размера
и
,
для которых выполняется соотношение:
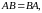 называются
перестановочными.
называются
перестановочными.
Обратная матрица.
Матрица
такая,
что
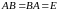 ,
называется обратной матрице
и обозначается
,
называется обратной матрице
и обозначается
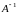 .
Таким
образом,
.
Таким
образом,
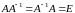
Необходимое и достаточное условия существования матрицы, обратной данной квадратной матрице.
Для того, чтобы
матрица
имела
обратную, необходимо и достаточно, чтобы
она была невырожденной
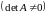 .
.
Ортогональная матрица.
Матрица
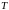 называется
ортогональной, если
называется
ортогональной, если
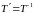 (т.е.
(т.е.
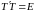 )
)
Степени квадратной матрицы.
Матрица
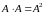 называется квадратом матрицы
.
Матрица
называется квадратом матрицы
.
Матрица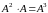 называется кубом матрицы
и т. д. Матрица
называется кубом матрицы
и т. д. Матрица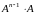
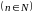 называется
называется
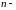 й
степенью матрицы
.
й
степенью матрицы
.
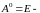 нулевой
степенью каждой квадратной матрицы
называется единичная матрица той же
размерности.
нулевой
степенью каждой квадратной матрицы
называется единичная матрица той же
размерности.
Целая
отрицательная степень
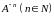 квадратной
матрицы
определяется
следующим образом:
квадратной
матрицы
определяется
следующим образом:
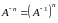 ,
где
,
где
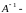 матрица,
обратная матрице
.
матрица,
обратная матрице
.
Нахождение
матрицы обратной квадратной невырожденной
матрице
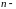 порядка.
порядка.
Если
дана квадратная невырожденная матрица
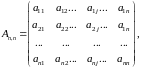 то
обратная ей матрица равна
то
обратная ей матрица равна
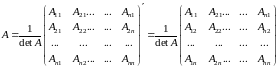 .
.
В
частности,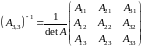 ,
где
,
где
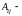 алгебраическое
дополнение элемента
алгебраическое
дополнение элемента
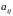 матрицы.
матрицы.
Элементарные преобразования матриц.
Элементарными преобразованиями матриц называются следующие операции:
1.Умножение
всех элементов некоторой строки на
число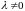 .
2.
Прибавление к элементам некоторой
строки соответственных элементов другой
строки, умноженной на произвольное
число.
3. Перемена местами строк
матрицы.
.
2.
Прибавление к элементам некоторой
строки соответственных элементов другой
строки, умноженной на произвольное
число.
3. Перемена местами строк
матрицы.
Эквивалентные матрицы.
Матрицы, полученные
одна из другой с помощью элементарных
преобразований называются эквивалентными.
Обозначение: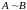
Свойства эквивалентных матриц.
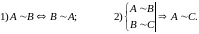
Ранг матрицы.
Если
все миноры матрицы
порядка
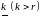 равны
нулю, а среди миноров порядка
равны
нулю, а среди миноров порядка
 имеется
хотя бы один, отличный от нуля, то
число
называется рангом матрицы
.
Обозначение
имеется
хотя бы один, отличный от нуля, то
число
называется рангом матрицы
.
Обозначение
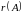 .
.
Ранги эквивалентных матриц.
Эквивалентные матрицы имеют один и тот же ранг. (Или: При элементарных преобразованиях ранг матрицы не из изменяется.)
Ранг ступенчатой матрицы.
Ранг ступенчатой матрицы равен числу ее ненулевых строк.
Матричные уравнения. Решения матричных уравнений.
Матричными уравнениями
называются уравнения вида
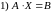 и
и
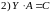 ,
где
,
где
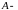 заданная,
невырожденная, квадратная матрица
порядка
;
заданная,
невырожденная, квадратная матрица
порядка
;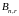 и
и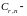 заданные
прямоугольные матрицы;
заданные
прямоугольные матрицы;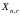 и
и
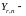 искомые
матрицы.
искомые
матрицы.
1) Решение уравнения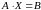 :
:
Матрица
невырожденная, поэтому существует
обратная матрица
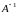 (
см. 12.3.). Умножим обе части уравнения
на матрицу
слева:
(
см. 12.3.). Умножим обе части уравнения
на матрицу
слева: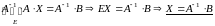 .
2) Решение уравнения
.
2) Решение уравнения
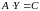 аналогично (самостоятельно):
аналогично (самостоятельно):
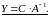
11) Системы
линейных уравнений.
Системы
линейных уравнений с
 неизвестными.
неизвестными.
Система вида
 ,
,
где
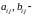 числа,
а
числа,
а
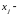 обозначение
неизвестных
обозначение
неизвестных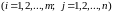 ,
называется системой
,
называется системой
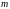 линейных
уравнений с
неизвестными.
Числа
называются
коэффициентами, а числа
линейных
уравнений с
неизвестными.
Числа
называются
коэффициентами, а числа
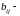 свободными
членами.
Короткая запись:
свободными
членами.
Короткая запись:
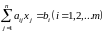 .
.
Совместные, несовместные системы. Определенная, неопределенная системы.
Система называется совместной, если у нее есть хотя бы одно решение, и несовместной, если она не имеет решения. Совместная система называется определенной, если у нее единственное решение, и неопределенной, если решений больше одного.
Элементарные преобразования системы.
Элементарными преобразованиями систем линейных уравнений называются следующие операции: 1.Умножение всех элементов некоторого уравнения на число . 2. Сложение соответственно левой и правой части двух уравнений, умноженных на какое-либо число, и замена одного из них полученным. 3. Перемена местами уравнений системы.
При элементарных преобразованиях множество решений системы не изменяется, т.е. системы, полученные одна из другой с помощью элементарных преобразований равносильны.
Решение систем линейных уравнений.
Метод обратной матрицы.
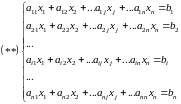 ,
,
Если в системе
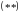 число
уравнений совпадает с числом
неизвестных, то она может быть записана
в матричной форме:
,
где
число
уравнений совпадает с числом
неизвестных, то она может быть записана
в матричной форме:
,
где
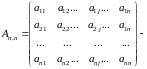 матрица
системы. Она составлена из коэффициентов
при неизвестных;
матрица
системы. Она составлена из коэффициентов
при неизвестных;
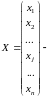 матрица-столбец неизвестных.
матрица-столбец неизвестных.
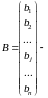 матрица-столбец свободных членов.
матрица-столбец свободных членов.

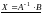
 ,
то матрица
имеет
обратную(См. 11.5.1.Теорема. ), и
,
то матрица
имеет
обратную(См. 11.5.1.Теорема. ), и
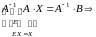 ,
поэтому решение
системы имеет вид:
,
поэтому решение
системы имеет вид:
Методы решения систем линейных уравнений: метод Крамера (формулы Крамера), метод Гаусса.
Метод Крамера.
Пусть дана система
линейных
уравнений с
неизвестными
(см.13.4.1). Пусть определитель матрицы
системы отличен от нуля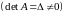 .
Обозначим
.
Обозначим
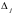 определитель
матрицы, полученный из матрицы
заменой
определитель
матрицы, полученный из матрицы
заменой
 го
столбца столбцом свободных членов.
Тогда система имеет единственное
решение, определяемое по формулам
Крамера:
го
столбца столбцом свободных членов.
Тогда система имеет единственное
решение, определяемое по формулам
Крамера:
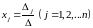
Доказательство (для системы трех уравнений с тремя неизвестными).
Формулы Крамера в случае системы трех уравнений с тремя неизвестными имеют вид:
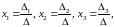 где
где
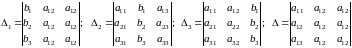 .
.
Решение системы
имеет вид (см. 13.4.1.1.)
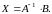
Метод Гаусса (метод
последовательного исключения неизвестных)
заключается в следующем: с помощью
элементарных преобразований в системе
линейных уравнений исключают неизвестное
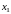 из всех уравнений, кроме первого, затем
из всех уравнений, кроме первого, затем
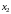 из всех уравнений, кроме второго, и
т. д.
из всех уравнений, кроме второго, и
т. д.
Теорема Кронекера-Капелли.
Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы системы равен рангу расширенной матрицы этой системы.
Система линейных однородных уравнений.
Система
линейных уравнений с
 неизвестными, у которой все свободные
члены равны нулю, называется системой
линейных однородных уравнений.
неизвестными, у которой все свободные
члены равны нулю, называется системой
линейных однородных уравнений.
Теорема о ненулевых решениях системы однородных уравнений.
Система линейных
однородных уравнений имеет ненулевые
решения тогда и только тогда, когда ранг
ее матрицы меньше числа неизвестных
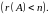
Свойства решений системы линейных однородных уравнений.
1) Если
столбец
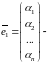 решение
системы (*), то столбец
решение
системы (*), то столбец
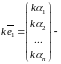 тоже
решение этой системы.
тоже
решение этой системы.
2) Если
столбцы
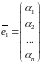 и
и
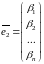 решения
системы (*), то столбец (линейная
комбинация столбцов
решения
системы (*), то столбец (линейная
комбинация столбцов
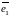 и
и
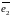 )
)
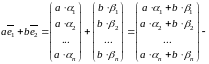 тоже
решение этой системы.
тоже
решение этой системы.
Фундаментальная система решений системы линейных уравнений.
Линейно
независимые решения
 линейной
системы называются фундаментальной
системой решений, если все решения
системы являются линейными комбинациями
столбцов
.
линейной
системы называются фундаментальной
системой решений, если все решения
системы являются линейными комбинациями
столбцов
.
Если
ранг
 матрицы
системы (*) меньше числа неизвестных
матрицы
системы (*) меньше числа неизвестных
 ,
то ее фундаментальная система решений
состоит из
,
то ее фундаментальная система решений
состоит из
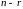 решений.
решений.
Общее
решение имеет вид:
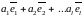 ,
где
,
где
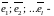 любая
фундаментальная система решений,
любая
фундаментальная система решений,
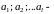 произвольные
числа и
произвольные
числа и
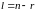 .
.
12) Линейное пространство. мерный вектор. Линейные операции с мерными векторами.
Множество
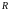 элементов (называемых векторами)
называется линейным (векторным)
пространством, если:
элементов (называемых векторами)
называется линейным (векторным)
пространством, если:
Указано правило, по
которому каждой паре элементов
(векторов )
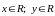 ставится в соответствие единственный
вектор
ставится в соответствие единственный
вектор
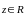 ,
который называется их суммой:
,
который называется их суммой:
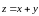 .
.
Указано правило, по
которому каждому числу
и любому вектору
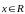 ставится в соответствие единственный
вектор
,
который называется произведением
вектора
ставится в соответствие единственный
вектор
,
который называется произведением
вектора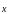 на число
:
на число
:
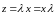
Свойства (аксиомы) линейных операций с векторами.
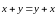 -коммутативное (переместительное)
свойство суммы.
-коммутативное (переместительное)
свойство суммы.
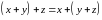 - ассоциативное (сочетательное)
свойство суммы.
- ассоциативное (сочетательное)
свойство суммы.
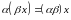 -ассоциативное относительно числового
множителя свойство.
-ассоциативное относительно числового
множителя свойство.
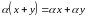 -
дистрибутивное (распределительное)
относительно суммы векторов свойство.
-
дистрибутивное (распределительное)
относительно суммы векторов свойство.
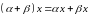 -
дистрибутивное относительно суммы
чисел свойство.
-
дистрибутивное относительно суммы
чисел свойство.
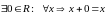 -
существует нулевой вектор.
-
существует нулевой вектор.
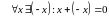 -
для любого вектора существует обратный
вектор.
-
для любого вектора существует обратный
вектор.
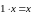 -произведение
единицы на любой вектор не изменяет
его.
-произведение
единицы на любой вектор не изменяет
его.
Определение линейного (векторного) пространства.
Если числа принадлежат множеству действительных чисел, то линейное пространство называется действительным (вещественным) линейным (векторным) пространством. Если числа принадлежат множеству комплексных чисел (См. 1.2. (1 семестр)), то линейное пространство называется комплексным линейным (векторным) пространством.
Линейная комбинация векторов линейного пространства.
Вектор
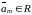 называется
линейной комбинацией векторов
называется
линейной комбинацией векторов
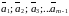 линейного
пространства
,
если существуют такие числа
линейного
пространства
,
если существуют такие числа
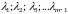 ,
что
,
что
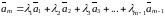
Линейно зависимые и линейно независимые векторы.
Векторы
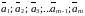 называются линейно зависимыми,
если существуют такие числа
называются линейно зависимыми,
если существуют такие числа ,
одновременно не равные 0, что
линейная комбинация векторов равна
нулю.
,
одновременно не равные 0, что
линейная комбинация векторов равна
нулю.
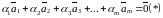 .
.
Если равенство
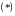 возможно только при
возможно только при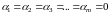 ,
то векторы
называются линейно независимыми.
,
то векторы
называются линейно независимыми.
Размерность и базис линейного пространства .
Совокупность
линейно независимых векторов
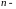 мерного
пространства
мерного
пространства
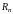 называется его базисом. Эти векторы
называются базисными.
называется его базисом. Эти векторы
называются базисными.
Теорема
о единственности представления вектора
в виде линейной комбинации базисных
векторов
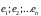 .
1.Пусть
векторы
образуют какой-нибудь базис
.
1.Пусть
векторы
образуют какой-нибудь базис
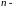 мерного
пространства
мерного
пространства
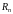 .
Для каждого вектора
этого пространства система
.
Для каждого вектора
этого пространства система
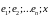 (состоящая
из
(состоящая
из
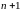 вектора)
линейно зависима. Следовательно,
существуют такие (одновременно не равные
нулю) числа
вектора)
линейно зависима. Следовательно,
существуют такие (одновременно не равные
нулю) числа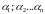 и
и
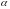 ,
что имеет место равенство:
,
что имеет место равенство:
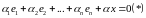 .
.
При этом
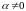 .
Если
.
Если
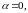 а хотя бы одно из чисел
отлично
от нуля, то векторы
а хотя бы одно из чисел
отлично
от нуля, то векторы
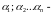 линейно
зависимы
линейно
зависимы
Из соотношения (*)
следует: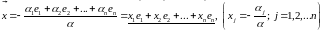 .
.
