
- •1. Свойство. 2. Свойство. 3. Свойство. .
- •6.1.4.4.Скалярное произведение равно произведению длины одного из векторов на проекцию другого на направление первого: .
- •6.1.4.5.Распределительный закон. .
- •6.4.2. 5. Смешанное произведение изменит знак при перестановке двух векторов.
- •8.2.3.2. Гиперболический цилиндр:
- •8.2.3.3. Параболический цилиндр:
1) Прямоугольная
декартова система координат
(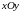 )
на плоскости: оси
координат, прямоугольная система
координат xOy
на плоскости; координаты точки: абсцисса
)
на плоскости: оси
координат, прямоугольная система
координат xOy
на плоскости; координаты точки: абсцисса ,
ордината
,
ордината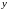 ;
знаки координат в четвертях, на которые
оси координат разбивают координатную
плоскость.
;
знаки координат в четвертях, на которые
оси координат разбивают координатную
плоскость.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве.
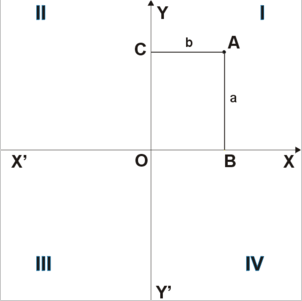
Прямоугольная
система координат на плоскости образуется
двумя взаимно перпендикулярными осями
координат ![]() и
и ![]() (крестом).
Оси координат пересекаются в точке
(крестом).
Оси координат пересекаются в точке ![]() ,
которая называется началом
координат,
на каждой оси выбрано положительное
направление.
,
которая называется началом
координат,
на каждой оси выбрано положительное
направление.
Координата ![]() называется абсциссой точки
называется абсциссой точки ![]() ,
координата
,
координата ![]() — ординатой точки
.
— ординатой точки
.
Четыре угла (I, II, III, IV), образованные осями координат и , называются координатными углами или квадрантами.
Точки внутри координатного угла I имеют положительные абсциссы и ординаты.
Точки внутри координатного угла II имеют отрицательные абсциссы и положительные ординаты.
Точки внутри координатного угла III имеют отрицательные абсциссы и ординаты
Точки внутри координатного угла IV имеют положительные абсциссы и отрицательные ординаты.
2) Перенос
начала координат и поворот декартовых
осей координат.
Формулы,
выражающие новые координаты точки через
старые и старые координаты точки через
новые.
Если осуществляется
перенос начала координат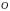 в новую точку
в новую точку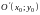 ,
с сохранением при этом прежнего
направления осей координат, то имеют
место следующие формулы
,
с сохранением при этом прежнего
направления осей координат, то имеют
место следующие формулы
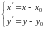 - новые
координаты точки через
старые
- новые
координаты точки через
старые
Формулы, выражающие новые координаты через старые.
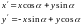 Формулы, выражающие старые
координаты через новые.
Формулы, выражающие старые
координаты через новые.
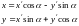
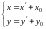 - старые
координаты точки через
новые.
Расстояние
от начала координат до точки.
Теорема.
Расстояние от начала координат до точки
- старые
координаты точки через
новые.
Расстояние
от начала координат до точки.
Теорема.
Расстояние от начала координат до точки
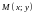 (точки
(точки
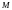 с координатами
с координатами и
и
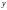 )
определяется по формуле:
)
определяется по формуле: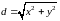 Расстояние
между точками.
Теорема.
Расстояние между точками
Расстояние
между точками.
Теорема.
Расстояние между точками
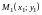 и
и
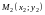 определяется по формуле:
определяется по формуле:
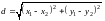 Деление
отрезка в заданном отношении.
Пусть
точка
Деление
отрезка в заданном отношении.
Пусть
точка
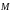 лежит
на прямой проходящей через точки
лежит
на прямой проходящей через точки
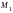 и
и
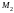 Точка
делит отрезок
Точка
делит отрезок
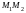 в отношении,
в отношении,
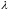 если
если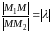 .
При этом
.
При этом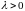 ,
если
,
если
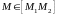 ,
и
,
и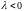 ,
если точка
,
если точка
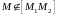 Разделить отрезок в отношении
- означает определить точку, которая
делит этот отрезок в отношени
.
Координаты
Разделить отрезок в отношении
- означает определить точку, которая
делит этот отрезок в отношени
.
Координаты
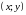 точки
,
которая делит отрезок
точки
,
которая делит отрезок
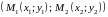 в отношении
,
определяются по формулам:
в отношении
,
определяются по формулам:
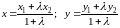
Координаты
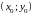 середины
середины
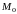 отрезка
определяются по формулам:
отрезка
определяются по формулам:
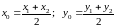
3) Полярные координаты.
На плоскости задаются (см. черт.)точка
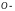 полюс,
исходящая из полюса полупрямая
полюс,
исходящая из полюса полупрямая
 полярная
ось,
масштаб (единица длины
полярная
ось,
масштаб (единица длины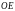 ).
).
П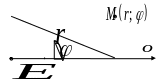 оложение
точки
на
плоскости определяется
оложение
точки
на
плоскости определяется
а) полярным радиусом
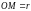 (расстоянием точки
от
полюса
).
(расстоянием точки
от
полюса
).
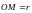 наз.
полярным радиус-вектором точки
наз.
полярным радиус-вектором точки
б) полярным углом
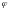 (углом, который образует отрезок
(углом, который образует отрезок
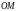 с
полярной осью).
с
полярной осью).
В этом случае говорят, что в
плоскости заданы полярные координаты
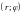 .
В полярных координатах точку
обозначают
записью:
.
В полярных координатах точку
обозначают
записью:
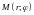 .
Замечание. Полярные координаты
называются основными, если введены
ограничения
.
Замечание. Полярные координаты
называются основными, если введены
ограничения
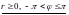 Связь между полярными и декартовыми
координатами точки.
Связь между полярными и декартовыми
координатами точки.
П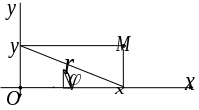 усть
полюс совпадает с началом
усть
полюс совпадает с началом
декартовой системы координат,
а полярная ось- с положительной
полуосью декартовой системы.
Формулы перехода (см. черт).
1)
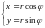 2)
2)
Замечание. Полярный
угол можно находить из уравнения: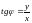 ,
но при этом нужно учитывать, что только
по тангенсу (без учета знаков
,
но при этом нужно учитывать, что только
по тангенсу (без учета знаков
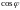 и
и
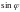 )
угол
)
угол
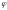 определить нельзя.
определить нельзя.
Поворот декартовых
осей координат.
Оси координат
повернуты на угол
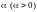 против часовой стрелки (см. черт.) и
образуют «новую»
систему
координат
против часовой стрелки (см. черт.) и
образуют «новую»
систему
координат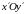 .
.
Пусть
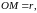 ось
ось
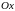 принята
за полярную ось и
принята
за полярную ось и

По формулам перехода (см. 1.5.2) получаем:
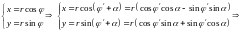
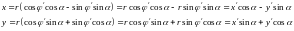
4) Прямая линия на плоскости.
2.1. 1.Определение. Линией
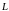 называется множество точек плоскости,
объединенных общим
свойством.
называется множество точек плоскости,
объединенных общим
свойством.
2.1. 2. Определение.
Пусть линия
отнесена
к декартовой системе координат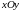 ,
и пусть
,
и пусть
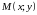 -
произвольная точка линии. Тогда
координаты
и
называются
текущими координатами точек линии.
-
произвольная точка линии. Тогда
координаты
и
называются
текущими координатами точек линии.
Уравнение линии.
Уравнение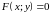 называется уравнением линии, если
уравнению
а) удовлетворяют
координаты всех точек, лежащих на линии
(после подстановки обращают его в
тождество);
б) не удовлетворяют
координаты никакой точки, не лежащей
на линии.
называется уравнением линии, если
уравнению
а) удовлетворяют
координаты всех точек, лежащих на линии
(после подстановки обращают его в
тождество);
б) не удовлетворяют
координаты никакой точки, не лежащей
на линии.
Уравнение прямой линии с угловым коэффициентом.
Угловой коэффициент:
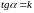
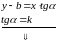
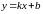 ─ уравнение прямой линии с угловым
коэффициентом.
─ уравнение прямой линии с угловым
коэффициентом.
Частные случаи расположения прямой на плоскости.
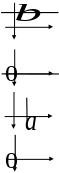
2.2.1.1.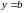 Прямая параллельна оси Ox.
Прямая параллельна оси Ox.
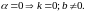
2.2.1.2.
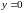 Прямая совпадает с осью Ox.
Прямая совпадает с осью Ox.
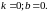
2.2.1.3.
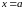 Прямая параллельна оси Oy.
Прямая параллельна оси Oy.
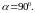 (Прямая не описывается уравнением
2.1.1.)
(Прямая не описывается уравнением
2.1.1.)
2.2.1.4.
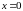 Прямая совпадает с осью Oy.
(
Прямая совпадает с осью Oy.
(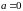 )
)
Угол между прямыми, заданными уравнениями с угловым коэффициентом.
Пусть прямые заданы уравнениями
с угловыми коэффициентами:
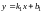 и
и
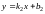
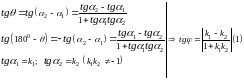
Общее уравнение прямой. Частные случаи.
Теорема. Всякое уравнение
первой степени, то есть уравнение вида
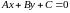 (кроме случая
(кроме случая
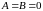 )
является уравнением прямой.
Частные случаи.
)
является уравнением прямой.
Частные случаи.
1.
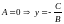 Прямая параллельна оси Ox.
Прямая параллельна оси Ox.
2.
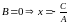 Прямая параллельна оси Oy.
Прямая параллельна оси Oy.
3.
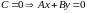 Прямая проходит через начало координат.
Прямая проходит через начало координат.
Угол между прямыми, заданными общими уравнениями.
Если прямые заданы
общими уравнениями с угловыми
коэффициентами:
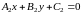 ,
то
,
то
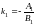 и
и
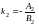 ,
поэтому
,
поэтому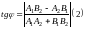 .
Замечание.
Формулой (2) можно пользоваться и в том
случае когда одна из прямых параллельна
оси Oy
.
Замечание.
Формулой (2) можно пользоваться и в том
случае когда одна из прямых параллельна
оси Oy
Условия
параллельности и перпендикулярности
этих прямых.
Условия
параллельности двух прямых
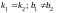 или
или
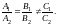 Условия
перпендикулярности двух прямых
Условия
перпендикулярности двух прямых
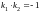 или
или

Уравнение прямой, проходящей через точку и имеющей заданный угловой коэффициент.
Пусть прямая задана точкой
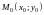 и направлением
и направлением
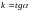 (направление
может быть задано с
помощью угла
или углового коэффициента).
(направление
может быть задано с
помощью угла
или углового коэффициента).
Уравнение прямой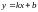 .Подставляем
координаты точки и получаем
.Подставляем
координаты точки и получаем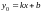 .
Отсюда
.
Отсюда
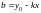 .
Подставив это значение в уравнение
прямой, получаем:
.
Подставив это значение в уравнение
прямой, получаем:
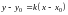 -
уравнение прямой, проходящей через
точку, и имеющей заданный угловой
коэффициент.
-
уравнение прямой, проходящей через
точку, и имеющей заданный угловой
коэффициент.
Уравнение пучка прямых.
При изменении
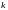 это
уравнение определяет множество прямых,
проходящих через точку
(кроме прямой, параллельной оси
Oy), и называется
уравнением пучка прямых.
это
уравнение определяет множество прямых,
проходящих через точку
(кроме прямой, параллельной оси
Oy), и называется
уравнением пучка прямых.
Уравнение прямой, проходящей через две точки.
Пусть прямая задана точками
и
.
Запишем уравнение прямой, проходящей
через
точку
: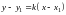 .
Значение углового коэффициента определим,
подставив координаты
точки
,
которая тоже лежит на этой прямой.
.
Значение углового коэффициента определим,
подставив координаты
точки
,
которая тоже лежит на этой прямой.
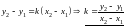 Уравнение прямой:
Уравнение прямой:
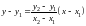 (см.
2.5.)или
(см.
2.5.)или
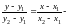
Уравнение прямой «в отрезках».
Пусть прямая пересекает оси
координат в точках:
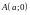 и
и
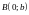 .Тогда
ее уравнение имеет вид
.Тогда
ее уравнение имеет вид
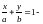
Уравнение прямой в полярных координатах.
П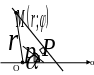 усть
прямая задана в полярной системе
координат а) длиной
усть
прямая задана в полярной системе
координат а) длиной
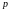 перпендикуляра
перпендикуляра
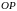 ,
проведенного из полюса
,
проведенного из полюса
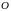 к
прямой, б) углом
к
прямой, б) углом
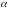 между
этим перпендикуляром и полярной осью.
между
этим перпендикуляром и полярной осью.
Составим уравнение, связывающее полярные
координаты
 и
и
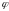 текущей
точки прямой
текущей
точки прямой
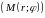 .
.
Из треугольника
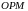 находим
находим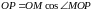 .
.
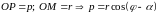 или
или
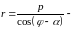
Нормальное уравнение прямой.
Уравнение
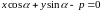 , где
, где
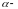 угол
между перпендикуляром, проведенным из
начала координат к прямой, а
угол
между перпендикуляром, проведенным из
начала координат к прямой, а
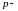 длина
этого перпендикуляра, называется
нормальным уравнением прямой.
длина
этого перпендикуляра, называется
нормальным уравнением прямой.
Приведение общего уравнения прямой к нормальному виду.
Пусть дано общее уравнение прямой
,
а ее нормальное уравнение имеет вид
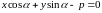 .
Так как оба уравнения являются уравнениями
одной и той же прямой, то то
существует число
.
Так как оба уравнения являются уравнениями
одной и той же прямой, то то
существует число
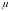 такое,
что
такое,
что
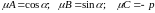 .
.
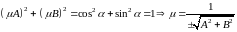 .
.
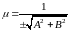 называется
нормирующим множителем. Так как
называется
нормирующим множителем. Так как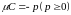 ,
то знак
,
то знак
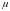 (знак
перед корнем) противоположен знаку
(знак
перед корнем) противоположен знаку
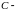 знаку
свободного члена уравнения.
знаку
свободного члена уравнения.
Таким образом, если прямая задана
общим уравнением
,
то ее нормальное уравнение
имеет
вид
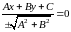 или
или
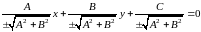
Р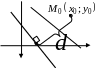 асстояние
от точки до прямой.
Формула
расстояния от точки
до прямой
:
асстояние
от точки до прямой.
Формула
расстояния от точки
до прямой
:
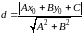
Параметрическое уравнение прямой.

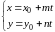 Здесь
Здесь
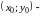 координаты точки
,
которая тоже лежит на этой прямой,
координаты точки
,
которая тоже лежит на этой прямой,
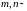 координаты
вектора, параллельного прямой
координаты
вектора, параллельного прямой
5) Кривые второго порядка.
Алгебраическая кривая.
Линия называется алгебраической кривой, если левая часть ее уравнения представляет многочлен относительно и . Степень этого многочлена называется порядком кривой.
Окружность.
Множество точек плоскости, равноудаленных от фиксированной точки той же плоскости (называемой центром) называется окружностью.
Уравнение окружности.
Уравнение
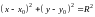 -
уравнение окружности радиуса
-
уравнение окружности радиуса
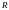 с
центром в точке
с
центром в точке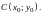 В частности уравнение
В частности уравнение
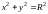 -
уравнение окружности радиуса
с
центром в начале координат.
-
уравнение окружности радиуса
с
центром в начале координат.
Эллипс. Определение.
Эллипсом называется множество точек плоскости, сумма расстояний которых от двух данных точек той же плоскости, называемых фокусами эллипса, есть величина постоянная.
Каноническое уравнение эллипса.
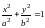
Форма
эллипса: большая и малая оси и полуоси,
вершины, фокальные радиусы.
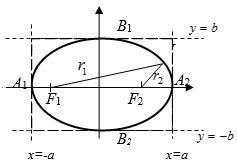
Числа
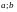 называются соответственно большой и
малой полуосями эллипса.
Точка
называются соответственно большой и
малой полуосями эллипса.
Точка
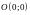 называется центром эллипса.
Точки
называется центром эллипса.
Точки
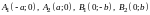 называются вершинами эллипса.
Точки
называются вершинами эллипса.
Точки
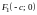 и
и
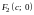 называются
фокусами эллипса.
называются
фокусами эллипса.
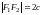 Если точка
лежит
на эллипсе, то отрезки
Если точка
лежит
на эллипсе, то отрезки
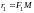 и
и
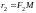 (а так же их длины) называются
фокальными радиусами точки
.
(а так же их длины) называются
фокальными радиусами точки
.
Соотношение между полуосями и половиной расстояния между фокусами.
Соотношение между
полуосями
и
половиной расстояния между фокусами
 (см(*))имеет
вид:
(см(*))имеет
вид:
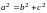
Уравнение
эллипса,
фокусы которого расположены на оси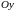 .
.
Фокусы эллипса
,
в уравнении которого
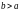 ,
расположены на оси
.
Соотношение между полуосями
и
половиной расстояния между фокусами
в
этом случае имеет
вид:
,
расположены на оси
.
Соотношение между полуосями
и
половиной расстояния между фокусами
в
этом случае имеет
вид:
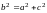 (фокусы эллипса расположены на
большой оси).
(фокусы эллипса расположены на
большой оси).
Гипербола. Определение.
Гиперболой называется множество точек плоскости, разность расстояний которых от двух данных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная.
Каноническое уравнение гиперболы.
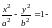
Форма гиперболы: действительная и мнимая оси и полуоси, вершины, фокальные радиусы.
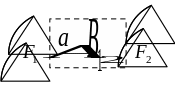
Отрезок
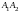 оси симметрии называется действительной,
а отрезок
оси симметрии называется действительной,
а отрезок
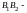 мнимой осями гиперболы.
мнимой осями гиперболы.
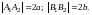
Числа
называются соответственно действительной
и мнимой полуосями гиперболы.
Точка
называется центром гиперболы.
Точки
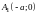 и
и
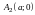 ,
лежащие на действительной оси
называются вершинами гиперболы.
Точки
и
называются
фокусами гиперболы
Если точка
лежит
на гиперболе, отрезки
и
(а так же их длины) называются
фокальными радиусами точки
.
,
лежащие на действительной оси
называются вершинами гиперболы.
Точки
и
называются
фокусами гиперболы
Если точка
лежит
на гиперболе, отрезки
и
(а так же их длины) называются
фокальными радиусами точки
.
Соотношение между полуосями и половиной расстояния между фокусами.
Соотношение между полуосями
и
половиной расстояния между фокусами
(см(**))имеет
вид:
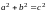 .
.
Асимптоты гиперболы. Уравнения асимптот гиперболы.
Асимптотой кривой
называется прямая линия к которой
неограниченно приближается уходящая
в бесконечность ветвь кривой.
Прямые
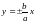 являются асимптотами гиперболы
являются асимптотами гиперболы
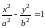 .
.
Равнобочная
(равносторонняя) гипербола.
Если
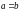 ,
то уравнение гиперболы имеет вид:
,
то уравнение гиперболы имеет вид:
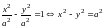 .
Асимптоты этой кривой образуют 450
с осями координат. Между собой они
перпендикулярны.
.
Асимптоты этой кривой образуют 450
с осями координат. Между собой они
перпендикулярны.
В этом
случае кривая называется равнобочной
(равносторонней) гиперболой
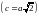 .
.
Параметрические
уравнения эллипса и гиперболы
Параметрическое
уравнение эллипса имеет вид: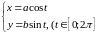 .
.
Параметрическое
уравнение гиперболы имеет вид: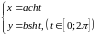 .
.
Парабола. Определение.
Пусть в плоскости заданы точка и прямая, не проходящая через точку. Параболой называется множество точек той же плоскости, расстояния которых от заданных в той же плоскости точки (фокуса параболы) и прямой (директрисы параболы) равны между собой.
Каноническое уравнение параболы.
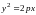
Форма параболы. Фокус и директриса параболы. Фокальный радиус.
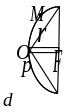
Фокусом параболы
является точка
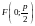 ,
директрисой – прямая
,
директрисой – прямая
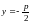 .
.
Если
точка
лежит
на параболе, отрезок
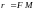 (а так же его длина) называется
фокальным радиусом точки
.
(а так же его длина) называется
фокальным радиусом точки
.
Эллипс, гипербола и парабола как конические сечения.
Сечение конуса плоскостью, параллельной двум образующим, является гиперболой.
Сечение конуса плоскостью, параллельной одной из образующих конуса, является параболой.
Сечение конуса плоскостью, угол наклона которой к оси конуса больше, чем угол между образующей конуса и его осью, является эллипсом.
Частный случай. Сечение конуса плоскостью, перпендикулярной оси конуса, является окружностью.
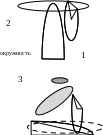
Исследование общего уравнения кривой 2-го порядка, не содержащего произведения координат.
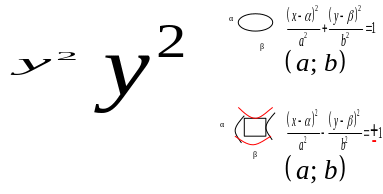
6) Координаты в пространстве.
Координатные
оси, координатные плоскости, октанты.
Абсцисса, ордината
и аппликата
 точки
в пространстве.
точки
в пространстве.
Координатные
оси определяют три координатные
плоскости:
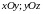 и
и
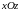 .
.
Координаты
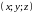 точки
точки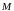 в пространстве определяются следующим
образом: через точку
проводят
три плоскости, параллельные координатным
плоскостям. Эти плоскости пересекают
оси координат соответственно в точках
в пространстве определяются следующим
образом: через точку
проводят
три плоскости, параллельные координатным
плоскостям. Эти плоскости пересекают
оси координат соответственно в точках
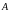 (ось
абсцисс),
(ось
абсцисс),
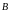 (ось
ординат) и
(ось
ординат) и
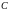 (ось
аппликат). Координаты этих точек на осях
называются соответственно координатами
точки: абсциссой
,
ординатой
и аппликатой
:
(ось
аппликат). Координаты этих точек на осях
называются соответственно координатами
точки: абсциссой
,
ординатой
и аппликатой
:
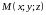 .
Между точками пространства и тройками
чисел установлено взаимно однозначное
соответствие.
.
Между точками пространства и тройками
чисел установлено взаимно однозначное
соответствие.
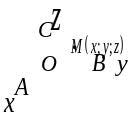

|
Октанты
Координаты |
І |
ІΙ |
ІІІ |
ІV |
V |
VІ |
VІІ |
VІІІ |
|
x
y
z |
+
+
+ |
─
+
+ |
─
─
+ |
+
─
+ |
+
+
─ |
─
+
─ |
─
─
─ |
+
+
─ |
Расстояние между точками в пространстве.
Расстояние
между точками
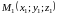 и
и
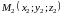 определяется по формуле:
определяется по формуле:
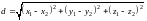
Формулы деления отрезка в заданном отношении.
Координаты
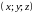 точки
,
которая делит отрезок
точки
,
которая делит отрезок
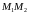
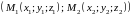 в отношении
в отношении
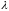 ,
определяются по формулам:
,
определяются по формулам:
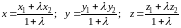
Координаты середины отрезка определяются по формулам:
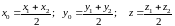
7) Векторная алгебра.
Сложение векторов (определение, свойства).
С ложение
векторов.
ложение
векторов.
Определение.
Вектор
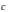 называется
суммой векторов
называется
суммой векторов
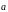 и
и

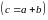 ,
если он находится последующему правилу:
,
если он находится последующему правилу:
Начало вектора совмещается с концом вектора , тогда начало вектора совпадает с началом вектора , его конец с концом вектора ( правило треугольника).
Свойства сложения векторов.
1) Сложение двух векторов можно производить по правилу параллелограмма:
Начала
векторов
и
совмещаются
,
тогда
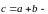 вектор,
который совпадает с диагональю
параллелограмма, построенного на
векторах
и
вектор,
который совпадает с диагональю
параллелограмма, построенного на
векторах
и
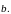 (Доказать
самостоятельно, что вектор, построенный
на данных векторах
и
по
правилу треугольника равен вектору,
построенному по правилу параллелограмма).
(Доказать
самостоятельно, что вектор, построенный
на данных векторах
и
по
правилу треугольника равен вектору,
построенному по правилу параллелограмма).
2) (Свойство
коммутативности) Сумма двух векторов
не изменится, если слагаемые поменять
местами:
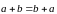
3) (Свойство
ассоциативности) Сумма трех векторов
подчиняется сочетательному закону:
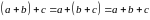
Вычитание векторов, противоположные векторы.
Вычитание векторов.
О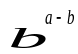 пределение.
Вектор
называется
разностью векторов
и
пределение.
Вектор
называется
разностью векторов
и
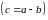 ,
если
,
если
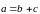 .
.
Если начала векторов
и
поместить в одну точку, то вектор
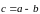 ─это
вектор, соединяющий конец вектора
с
концом вектора
(«
из конца вычитаемого в конец
уменьшаемого»).
─это
вектор, соединяющий конец вектора
с
концом вектора
(«
из конца вычитаемого в конец
уменьшаемого»).
а).
Замечание.
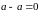 .
.
б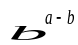 ).
Замечание. Если сумма двух векторов
равна нулю
).
Замечание. Если сумма двух векторов
равна нулю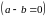 ,
то они называются противоположными:
,
то они называются противоположными:
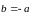 .
.
Умножение вектора на число (определение, свойства).
Умножение вектора на число.
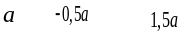
Определение.
Произведение
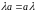 вектора
вектора
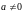 на число
на число
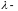 это
вектор, длина которого равна
это
вектор, длина которого равна
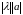 ,
а направление совпадает с направлением
вектора
,
если
и
противоположно направлению вектора
,
при
.
Вектор
,
а направление совпадает с направлением
вектора
,
если
и
противоположно направлению вектора
,
при
.
Вектор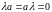 ,
если
,
если
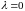 .
.
Замечание. Операции сложения векторов и умножение вектора на число называются линейными операциями с векторами.
Свойства линейных операций с векторами.
1.
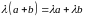 ;
2.
;
2.
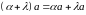 .
.
3.
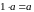 .
4.
.
4.
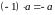 .
5.
.
5.
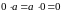 .
Коллинеарность
векторов. Определение.
.
Коллинеарность
векторов. Определение.
Два вектора называются коллинеарными, если они лежат на одной прямой (или параллельны одной прямой).
Необходимое и достаточное условие коллинеарности двух векторов.
Для того,
чтобы два вектора
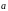 и
и
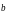 были
коллинеарными, необходимо и достаточно,
чтобы для них выполнялось условие:
были
коллинеарными, необходимо и достаточно,
чтобы для них выполнялось условие:
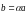 .
.
Компланарность векторов. Определение.
Три вектора называются компланарными, если они лежат в одной плоскости (или параллельны одной плоскости).
Необходимое и достаточное условие компланарности трех векторов.
Для того, чтобы три
вектора были компланарны, необходимо
и достаточно, чтобы для них выполнялось
условие:
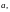 и
и
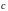 связаны формулой:
связаны формулой:
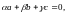 где хотя бы одно из чисел
где хотя бы одно из чисел
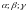 отлично
от нуля.
отлично
от нуля.
Разложение вектора по двум неколлинеарным направлениям.
Р азложением
вектора
по
двум неколлинеарным направлениям
(векторам)
и
,
расположенным в одной плоскости с
ним, называется его представление
в виде
азложением
вектора
по
двум неколлинеарным направлениям
(векторам)
и
,
расположенным в одной плоскости с
ним, называется его представление
в виде
![]() Пусть
даны три компланарных вектора (
и
),
тогда
Пусть
даны три компланарных вектора (
и
),
тогда
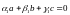 Пусть
Пусть
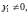 тогда
тогда
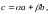 где
где
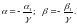 Задача разложения вектора по
двум неколлинеарным направлениями
имеет единственное решение.
Задача разложения вектора по
двум неколлинеарным направлениями
имеет единственное решение.
Разложение вектора по трем некомпланарным направлениям.
Р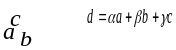 азложением
вектора
азложением
вектора
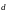 по трем некомпланарным
направлениям (векторам)
,
и
называется его представление в виде
по трем некомпланарным
направлениям (векторам)
,
и
называется его представление в виде
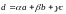
Задача разложения вектора по трем некомпланарным направлениями имеет единственное решение.
Проекция вектора на ось.
Пусть
дана произвольная ось U
и вектор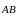 .
Из точек
и
проведены
перпендикуляры до пересечения с осью
в точках
.
Из точек
и
проведены
перпендикуляры до пересечения с осью
в точках
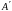 и
и
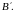 Точка
называется
проекцией точки
,
а точка
Точка
называется
проекцией точки
,
а точка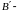 проекцией точки
на
ось, а величина отрезка
проекцией точки
на
ось, а величина отрезка
 ,
взятая со знаком «+», если угол между
вектором и осью острый, и со знаком «─»,
если угол тупой, называется проекцией
вектора
на ось U :
,
взятая со знаком «+», если угол между
вектором и осью острый, и со знаком «─»,
если угол тупой, называется проекцией
вектора
на ось U :
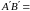 Пр
Пр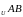 .
.
Проекция вектора на ось не зависит от точки его приложения.
Свойства проекций векторов на ось.
1. Свойство. 2. Свойство. 3. Свойство. .
Проекция вектора на другой вектор.
Проекция
вектора на другой вектор (проекция
вектора
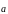 на направление вектора
на направление вектора
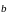 ):
):
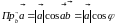 (аналогично определению проекции вектора
на ось).
(аналогично определению проекции вектора
на ось).
Очевидно, что проекция вектора на вектор обладает теми же свойствами, что и проекция вектора на ось.
Координаты вектора. Определение.
Если
,
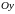 и
и
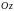 -
оси координат, то числа
-
оси координат, то числа
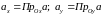 и
и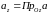 называются координатами
вектора
.
Запись:
называются координатами
вектора
.
Запись:
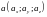 Замечание.
Координаты вектора не зависят от точки
его приложения.
Замечание.
Координаты вектора не зависят от точки
его приложения.
Длина вектора в координатной форме.
Длина
вектора выражается через его
координаты по формуле:
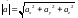
Координаты вектора, если заданы координаты его начала и конца.
Координаты
вектора
определяются формулами:
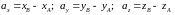 (Из
координаты конца вектора вычитается
координата его начала)
(Из
координаты конца вектора вычитается
координата его начала)
Координатные орты.
Единичные векторы,
направления которых совпадают с
положительными направлениями координатных
осей, называются координатными
ортами.
Обозначение:

Направляющие косинусы вектора и соотношение между ними.
Косинусы углов между вектором и координатными ортами называются направляющими косинусами:
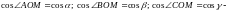 Направляющие
косинусы вектора связаны соотношением:
Направляющие
косинусы вектора связаны соотношением:
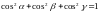 .
.
Линейные операции с векторами в координатной форме: равенство векторов, умножение вектора на число, сложение векторов.
Пусть
векторы заданы своими координатами:
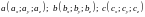 ,
тогда
,
тогда
Равенство векторов в координатной форме:
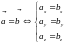 (Если векторы равны, то равны их
соответствующие координаты).
(Если векторы равны, то равны их
соответствующие координаты).
Умножение вектора на число в координатной форме:
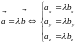 (При умножении вектора на число каждая
его координата умножается на это
число).
(При умножении вектора на число каждая
его координата умножается на это
число).
Сложение векторов в координатной форме:
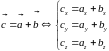 (При сложении векторов их соответствующие
координаты складываются).
(При сложении векторов их соответствующие
координаты складываются).
Необходимое и достаточное условие коллинеарности двух векторов.
Два вектора коллинеарны тогда только тогда, когда их координаты пропорциональны.
Радиус-вектор точки. Определение.
Радиус-вектор
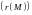 точки
точки
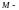 это
связанный вектор, начало которого
находится в точке
это
связанный вектор, начало которого
находится в точке
 (в начале координат), а конец- в точке
.
(в начале координат), а конец- в точке
.
Координаты радиус-вектора.
Координаты радиус-вектора точки совпадают с координатами точки :
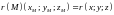
Скалярное произведение векторов. Определение.
Скалярным
произведением
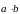 двух
векторов
и
называется
произведение длин (модулей) этих векторов
на косинус угла между ними:
двух
векторов
и
называется
произведение длин (модулей) этих векторов
на косинус угла между ними:
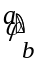
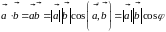
Физический (механический) смысл.
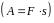
Свойства скалярного произведения.
6.1.4.1. Скалярное произведение равно нулю в одном из следующих случаев:
а) векторы перпендикулярны;
б) один из сомножителей (или оба) является нулевым вектором
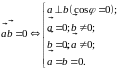
6.1.4.2.
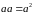 называется
скалярным квадратом вектора.
называется
скалярным квадратом вектора.
Скалярный
квадрат вектора равен квадрату его
длины, и длина вектора равна корню
квадратному из его скалярного
квадрата.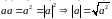 .
.
6.1.4.3.
Переместительный закон. Скалярное
произведение не меняется при перестановке
сомножителей:
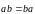 .
.
