Задача № 6

Среднегодовая численность занятых в экономике РФ характеризуется следующими данными:

Годы	1992	1993	1994	1995	1996	1997	1998	1999	2000
Среднегодовая численность занятых	71,1	68,8	64,8	66,4	66,0	64,7	63,8	64,0	64,3

Выявить основную тенденцию занятых в экономике РФ методом аналитического выравнивания.

Решение:

Построим линейную модель временного ряда методом аналитического выравнивания:

а) для среднегодовой численности занятых в экономике РФ..

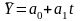, где t- порядковый номер периода времени.

Параметры уравнения тренда «a» и «b» находятся решением системы нормальных уравнений прямой:¹

Расчет параметров тренда выполнен с использованием вспомогательной таблицы. Подставляя полученные суммы в систему уравнений

,

получаем а₀ = 593,9 / 9 = 65,99; а₁ = -45,3/260 = 0,755

Отсюда искомое уравнение тренда:.ŷ₁ = 65,99 - 0,755*t

Подставляя в это уравнение значения t:, находим выравненные (теоретические) значения ŷ_t.

Расчет параметров тренда выполнен с использованием вспомогательной таблицы.

Вспомогательная таблица

Период времени	Объем производства, у	Услов. обозн. периодов времени,t	t·у	t²	Теоретич. значения объема производства
1992	71,1	-4	-284,4	16	69,0
1993	68,8	-3	-206,4	9	68,3
1994	64,8	-2	-129,6	4	67,5
1995	66,4	-1	-66,4	1	66,7
1996	66,0	0	0	0	66,0
1997	64,7	1	64,7	1	65,2
1998	63,8	2	127,6	4	64,5
1999	64,0	3	192,0	9	63,7
2000	64,3	4	257,2	16	63,0
итого	593,9	0	-45,3	60	593,9

Задача № 7

Имеются данные о продаже мяса на рынках города:

№ рынка	Январь			Февраль
	Цена за 1 кг.	Продано, кг.	Цена за 1 кг.		Продано, кг.
1	125	600	127		1000
2	118	400	128		500

Вычислить:

1) Индекс переменного состава;

2) Индекс цен постоянного состава;

3) Индекс структурных сдвигов.

Показать взаимосвязь индексов. Сделать выводы.

Решение:

1. Индекс переменного состава:

где р₀, q₀ – цена и объем продаж в январе;

р_1, q₁ – цена и объем продаж в феврале.

2. Индекс себестоимости постоянного (фиксированного) состава рассчитаем по следующей формуле:

3. Индекс структурных сдвигов:

Индекс постоянного состава характеризует среднее изменение самого усредняемого признака (цены) при постоянстве структуры совокупности (объема продаж).

Индекс структурных сдвигов показывает, в какой степени изменение средней величины индексируемого показателя (цены) произошло за счет изменения структуры (объема продаж) совокупности.

Индекс переменного состава показывает изменение, как за счет усредняемого признака, так и за счет состава совокупности.

Следовательно, 1,563 = 1,038 * 1,506