Задача № 4

По данным выборочного обследования пробега шин одного типоразмера в городских условиях оценить их ходимость при работе водителей различной квалификации, рассчитав показатели среднего пробега, среднее квадратическое отклонение, коэффициент вариации, коэффициент сравнения.

Пробег автомобильных шин, тыс. км.	При работе водителя I класса	При работе водителяII класса
50-52	2	10
52-54	6	26
54-56	18	10
56-58	10	8
58-60	4	6
Итого	40	60

Решение:

Рассчитаем средний пробег шин при работе водителей разной квалификации, определив для этого среднее значение пробега

Пробег автомобильных шин, тыс. км.	При работе водителя I класса	При работе водителяII класса
51	2	10
53	6	26
55	18	10
57	10	8
59	4	6
Итого	40	60

Для водителей I класса

	f
19,36	2	38,72
5,76	6	34,56
0,16	18	2,88
2,56	10	25,6
12,96	4	51,84
Хср=55,4	40	153,6

Коэффициент вариации:

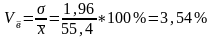
Для водителей II класса

	f
9,82	2	19,64
1,28	6	7,71
0,75	18	13,52
8,22	10	82,18
23,68	4	94,74
Хср=54,13	60	217,78

Коэффициент вариации:

Коэффициент сравнения пробега шин при работе водителей I и II классов.:

К_ср = 55,4 / 54,13 * 100 = 102,35

По среднеквадратическому отклонению: 1,96 / 1,905 = 1,029.

По коэффициенту вариации: 3,54 / 3,52 = 1,005.

Следовательно, все полученные данные у водителей первого класса выше.

Задача № 5

Из готовой продукции в порядке собственно случайного бесповторного отбора было отобрано 200 единиц, из которых 8 оказалось браком. Можно ли полагать с вероятностью 0,954, что потери продукции не превышают 5%, если выборка составляет двадцатую часть ее размера.

Решение:

При бесповторном отборе предельная ошибка выборки определяется по формуле: Δ=t*µ, где t – коэффициент доверия, т.е. показатель зависящий от вероятности Р, с которой предельная ошибка определяется. Для Р= 0,954, t = 2.

Предельная ошибка выборки для бесповторного отбора определяется по формуле:

,

где - среднеквадратическое отклонение;

n/N = 0,2 – или 20-я часть выборки.

Среднеквадратическое отклонение определяется следующим образом:

р = 8 / 200 = 0,04 =0.04*(1-0.04) =0.0384

Определим предельную ошибку:

или 2,48 %

Следовательно потери продукции не будут превышать 5 %.