В результате изучения дисциплины «Математическое моделирование» магистранты должны:

знать: свойства математических моделей, их типы, принципы и способы построения; основные элементы теории проверки статистических гипотез; критерии значимости параметров; построение наиболее мощных критериев.

уметь: разрабатывать алгоритмы реализации математических моделей, пользоваться математической литературой для самостоятельного изучения вопросов, связанных с профессиональной деятельностью;

владеть: основами теории моделирования и эксперимента, методами построения математических моделей для решения задач, возникающих в профессиональной деятельности.

Процесс изучения дисциплины направлен на формирование следующих компетенций (ФГОС ВПО, 2009):

общекультурные (ОК):

- способность совершенствовать и развивать свой интеллектуальный и общекультурный уровень (ОК - 1);

- способность к самостоятельному обучению новым методам исследования, к изменению научного и научно-производственного профиля своей профессиональной деятельности (ОК - 2);

- способность самостоятельно приобретать с помощью информационных технологий и использовать в практической деятельности новые знания и умения (ОК - 6);

- способность собирать, обрабатывать с использованием современных информационных технологий и интерпретировать необходимые данные для формирования суждений по соответствующим научным проблемам.

профессиональные (ПК):

- способность проводить расчеты и определять экономическую и социальную эффективность исследований и разработок.

1. Основы математического моделирования

1.1. Понятие математической модели

С середины XX в. в самых различных областях человеческой деятельности стали широко применять математические методы и ЭВМ. Возникли такие новые дисциплины, такие как «математическая экономика», «математическая химия», «математическая лингвистика» и т. д., изучающие математические модели соответствующих объектов и явлений, а также методы исследования этих моделей.

Моделирование представляет собой один из основных методов познания, является формой отражения действительности и заключается в выяснении или воспроизведении тех или иных свойств реальных объектов, предметов и явлений с помощью других объектов, процессов, явлений, либо с помощью абстрактного описания в виде изображения, плана, схемы, совокупности уравнений, неравенств, алгоритмов и программ. Возможности моделирования, то есть перенос результатов, полученных в ходе построения и исследования модели, на оригинал основаны на том, что модель в определенном смысле отображает (воспроизводит, моделирует, описывает, имитирует) некоторые интересующие исследователя черты объекта.

Вычислительные эксперименты, проводимые на основе математических моделей, помогают увидеть за частным общее, развить универсальные методы анализа объектов различной физической природы, познать свойства изучаемых процессов и систем. Приведем несколько примеров.

1. Задачи о движении снаряда.

Снаряд пущен с Земли с начальной скоростью v₀ = 30 м/с под углом = 45° к ее поверхности. Требуется найти траекторию его движения и расстояние S между начальной и конечной точкой этой траектории.

Пренебрегая размерами снаряда, будем считать его материальной точкой. Введем систему координат xOy, совместив ее начало O с исходной точкой, из которой пущен снаряд, ось x направим горизонтально, а ось y — вертикально (Рис. 1).

Рис. 1

Тогда движение снаряда описывается формулами:

,

где t – время, g 10 м/с² — ускорение свободного падения. Эти формулы и дают математическую модель поставленной задачи. Выражая t через x из первого уравнения и подставляя во второе, получим уравнение траектории движения снаряда: .

Эта кривая (парабола) пересекает ось x в двух точках: (начало траектории) и (место падения снаряда). Подставляя в полученные формулы заданные значения v₀ = 30 м/с и = 45°, получим , м.

Отметим, что при построении этой модели использован ряд предположений: например, что Земля плоская, а воздух и вращение Земли не влияют на движение снаряда.

2) Задача о баке с наименьшей площадью поверхности. 

Требуется найти высоту h₀ и радиус r₀ жестяного бака объема V = 30 м³, имеющего форму закрытого кругового цилиндра, при которых площадь его поверхности S минимальна (в этом случае на его изготовление пойдет наименьшее количество жести).

Объем (V) и площадь поверхности (S) цилиндра высоты h и радиуса r можно вычислить по формулам: .

Выражая h через r и V из первой формулы и подставляя полученное выражение во вторую, получим: .

Таким образом, с математической точки зрения, задача сводится к определению такого значения r, при котором достигает своего минимума функция S(r). Найдем те значения r₀, при которых производная функции S(r), равная , обращается в нуль. Это достигается при . Можно проверить, что вторая производная функции S(r) меняет знак с минуса на плюс при переходе аргумента r через точку r₀. Следовательно, в точке r₀ функция S(r) имеет минимум. Соответствующее значение h₀ = 2r₀. Подставляя в выражение для r₀ и h₀ заданное значение V, получим искомый радиус и высоту .

3) Транспортная задача. 

В городе имеются два склада муки и два хлебозавода. Ежедневно с первого склада вывозят 50 т муки, а со второго – 70 т на заводы, причем на первый – 40 т, а на второй – 80 т.

Обозначим через a_ij стоимость перевозки 1 т муки с i-го склада на j-й завод (i, j = 1,2). Пусть a₁₁ = 1,2 р., a₁₂ = 1,6 р., a₂₁ = 0,8 р., a₂₂ = 1 р.

Как нужно спланировать перевозки, чтобы их стоимость была минимальной?

Придадим задаче математическую формулировку. Обозначим через x₁ и x₂ количество муки, которое надо перевезти с первого склада на первый и второй заводы, а через x₃ и x₄ – со второго склада на первый и второй заводы соответственно. Тогда

(1)

Общая стоимость всех перевозок определяется формулой

f = 1,2x₁ + 1,6x₂ + 0,8x₃ + x₄.

С математической точки зрения, задача заключается в том, чтобы найти четыре числа x₁, x₂, x₃ и x₄, удовлетворяющие всем заданным условиям и дающим минимум функции f. Решим систему уравнений (1) относительно x_i (i = 1, 2, 3, 4) методом исключения неизвестных. Получим, что

(2)

x₄ не может быть определено однозначно. Так как x_i 0 (i = 1, 2, 3, 4), то из системы уравнений (2) следует, что . Подставляя выражение для x₁, x₂, x₃ в формулу f, получим

f = 148 – 0,2x₄.

Минимум функции достигается при максимально возможном значении x₄, то есть при x₄ = 70. Соответствующие значения других неизвестных определяются по формулам (2): x₁ = 40, x₂ = 10, x₃ = 0.

4) Задача о радиоактивном распаде.

Пусть N(0) — исходное количество атомов радиоактивного вещества, а N(t) — количество нераспавшихся атомов в момент времени t. Экспериментально установлено, что скорость изменения количества этих атомов N'(t) пропорциональна N(t), то есть константа радиоактивности данного вещества. Решение этого дифференциального уравнения имеет вид . Время T, за которое число исходных атомов уменьшилось вдвое, называется периодом полураспада, и является важной характеристикой радиоактивности вещества. Для определения T надо положить в формуле . Тогда . Например, для радона и, следовательно, T = 3,15 суток.

5) Задача о коммивояжере.

Коммивояжеру, живущему в городе A₁, надо посетить города A₂, A₃ и A₄, причем каждый город точно один раз, и затем вернуться обратно в A₁. Известно, что все города попарно соединены между собой дорогами, причем длины дорог b_ij между городами A_i и A_j (i, j = 1, 2, 3, 4) таковы:

b₁₂ = 30, b₁₄ = 20, b₂₃ = 50, b₂₄ = 40, b₁₃ = 70, b₃₄ = 60.

Надо определить порядок посещения городов, при котором длина соответствующего пути минимальна.

Изобразим каждый город точкой на плоскости и пометим ее соответствующей меткой A_i (i = 1, 2, 3, 4). Соединим эти точки отрезками прямых: они будут изображать дороги между городами. Для каждой «дороги» укажем ее протяженность в километрах (Рис. 2).

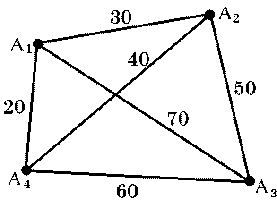
Рис. 2

Получился граф – математический объект, состоящий из некоторого множества точек на плоскости (называемых вершинами) и некоторого множества линий, соединяющих эти точки (называемых ребрами). Более того, этот граф меченый, так как его вершинам и ребрам приписаны некоторые метки — числа (ребрам) или символы (вершинам). Циклом на графе называется последовательность вершин А₁, А₂, ..., А_k, такая, что вершины А₁, ..., А_k – различны, а любая пара вершин А_i, А_i+1 (i = 1, ..., k – 1) и пара А₁, А_k соединены ребром. Таким образом, рассматриваемая задача заключается в отыскании такого цикла на графе, проходящего через все четыре вершины, для которого сумма всех весов ребер минимальна. Найдем перебором все различные циклы, проходящие через четыре вершины и начинающиеся в A₁:

1. A₁, A₄, A₃, A₂, A₁;

2. A₁, A₃, A₂, A₄, A₁;

3. A₁, A₃, A₄, A₂, A₁.

Найдем теперь длины этих циклов (в км): L₁ = 160, L₂ = 180, L₃ = 200. Итак, маршрут наименьшей длины – это первый.

Заметим, что если в графе n вершин и все вершины попарно соединены между собой ребрами (такой граф называется полным), то число циклов, проходящих через все вершины, равно Следовательно, в нашем случае имеется ровно три цикла.

6) Задача о нахождении связи между структурой и свойствами веществ.

Рассмотрим несколько химических соединений, называемых нормальными алканами. Они состоят из n атомов углерода и n + 2 атомов водорода (n = 1, 2 ...), связанных между собой так, как показано на рисунке 3 для n = 3.

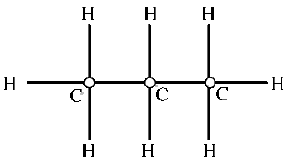
Рис. 3

Пусть известны экспериментальные значения температур кипения этих соединений:

y_э(3) = – 42°, y_э(4) = 0°, y_э(5) = 28°, y_э(6) = 69°.

Требуется найти приближенную зависимость между температурой кипения и числом n для этих соединений. Предположим, что эта зависимость имеет вид , где a, b – константы, подлежащие определению. Для нахождения a и b подставим в эту формулу последовательно n = 3, 4, 5, 6 и соответствующие значения температур кипения. Имеем:

Для определения наилучших a и b существует много разных методов. Воспользуемся наиболее простым из них. Выразим b через a из этих уравнений:

Возьмем в качестве искомого b среднее арифметическое этих значений, то есть, положим . Подставим в исходную систему уравнений это значение b и, вычисляя a, получим следующие значения: . Возьмем в качестве искомого a среднее значение этих чисел, то есть положим . Итак, искомое уравнение имеет вид .

Проверим точность модели на исходных четырех соединениях, для чего вычислим температуры кипения по полученной формуле:

y_р(3) = – 37⁰, y_р(4) = – 3⁰, y_р(5) = 31⁰, y_р(6) = 65⁰.

Таким образом, ошибка расчетов данного свойства для этих соединений не превышает 5°. Используем полученное уравнение для расчета температуры кипения соединения с n = 7, не входящего в исходное множество, для чего подставим в это уравнение n = 7: y_р(7) = 99°. Результат получился довольно точный: известно, что экспериментальное значение температуры кипения y_э(7) = 98°.

7) Задача об определении надежности электрической цепи.

Рассмотрим пример вероятностной модели. Сначала приведем некоторые сведения из теории вероятностей – математической дисциплины, изучающей закономерности случайных явлений, наблюдаемых при многократном повторении опыта. Назовем случайным событием A возможный исход некоторого опыта. События A₁, ..., A_k образуют полную группу, если в результате опыта обязательно происходит одно из них. События называются несовместными, если они не могут произойти одновременно в одном опыте. Пусть при n-кратном повторении опыта событие A произошло m раз. Частотой события A называется число . Очевидно, что значение W нельзя предсказать точно до проведения серии из n опытов. Однако природа случайных событий такова, что на практике иногда наблюдается следующий эффект: при увеличении числа опытов значение практически перестает быть случайным и стабилизируется около некоторого неслучайного числа P(A), называемого вероятностью события A. Для невозможного события (которое никогда не происходит в данном опыте) P(A)=0, а для достоверного события (которое всегда происходит в данном опыте) P(A)=1. Если события A₁, ..., A_k образуют полную группу попарно несовместимых событий, то P(A₁)+...+P(A_k)=1.

Пусть, например, опыт состоит в подбрасывании игральной кости и наблюдении числа выпавших очков X. Тогда можно ввести следующие случайные события A_i ={X = i}, i = 1, ..., 6. Они образуют полную группу попарно несовместных равновероятных событий, поэтому P(A_i) , где i = 1, ..., 6 равны между собой.

Суммой событий A и B называется событие A + B, состоящее в том, что в опыте происходит хотя бы одно из них. Произведением событий A и B называется событие AB, состоящее в одновременном появлении этих событий. Для независимых событий A и B верны формулы:

, (если события А и В несовместны, то последняя формула примет вид: ).

Рассмотрим теперь следующую задачу. Предположим, что в электрическую цепь последовательно включены три элемента, работающие независимо друг от друга. Вероятности отказов 1-го, 2-го и 3-го элементов соответственно равны P₁ = 0,1, P₂ = 0,15, P₃ = 0,2. Будем считать цепь надежной, если вероятность того, что в цепи не будет тока, не более 0,4. Требуется определить, является ли данная цепь надежной.

Так как элементы включены последовательно, то тока в цепи не будет (событие A), если откажет хотя бы один из элементов. Пусть A_i – событие, заключающееся в том, что i-й элемент работает (i = 1, 2, 3). Тогда P(A₁) = 0,9, P(A₂) = 0,85, P(A₃) = 0,8. Очевидно, что A₁A₂A₃ — событие, заключающееся в том, что одновременно работают все три элемента, и .

Тогда , поэтому P(A) = 0,388 < 0,4. Следовательно, цепь является надежной.

Отметим, что приведенные примеры математических моделей (среди которых есть функциональные и структурные, детерминистические и вероятностные) носят иллюстративный характер и, очевидно, не исчерпывают всего разнообразия математических моделей, возникающих в естественных и гуманитарных науках.

Моделирование как форма отражения действительности широко распространено, и достаточно полная классификация возможных видов моделирования крайне затруднительна, хотя бы в силу многозначности понятия "модель", широко используемого не только в науке и технике, но и в искусстве, и в повседневной жизни. В каждой из этих областей моделирование имеет свои особенности.

Термин «модель» используют для обозначения:

1. устройства, воспроизводящего строение или действие какого-либо другого устройства (уменьшенное, увеличенное или в натуральную величину);

2. аналога (чертежа, графика, плана, схемы, описания и т.д.) какого либо явления, процесса или предмета.

В научной литературе распространены два значения термина «модель»:

1) модель как аналог реального объекта;

2) модель как образец будущего изделия.

Далее моделирование мы будем рассматривать применительно к научным исследованиям. Рассмотрим некоторые подходы к определению понятия модели. Модель (фр. modèle, от лат. modulus – мера, аналог, образец)  – физически реальный или информационный объект, созданный искусственно или выбранный из реального мира, способный на определенных этапах познания, замещать другие объекты, называемыми оригиналом, и давать об этом оригинале новую информацию в соответствии с целями и задачами моделирования [14]. Под моделью понимают также такой материальный или мысленно представляемый объект, который в процессе познания (изучения) замещает объект – оригинал, сохраняя некоторые важные для данного исследования типичные его черты.

В. А. Штофф под моделью понимает такую мысленно представляемую или материально реализуемую систему, которая отображая или воспроизводя объект исследования, способна замещать его так, что ее изучение дает нам новую информацию об этом объекте [13].

Процесс построения и использования модели называется моделированием. Основная цель моделирования – исследовать объекты и предсказать результаты будущих наблюдений. Однако, моделирование  – это также метод познания окружающего мира, который можно отнести к общенаучным методам, применяемым как на эмпирическом (экспериментальном), так и на теоретическом уровне познания. В связи с этим условно выделяют материальные и идеальные модели. Материальное моделирование – это моделирование, при котором исследование объекта проводится при использовании его материального аналога, воспроизводящего основные физические, геометрические, динамические и функциональные характеристики данного объекта (например, использование макетов в архитектуре). Идеальное моделирование отличается от материального тем, что оно носит теоретический характер и основано на аналогии идеальной (не материализованной). В свою очередь, идеальное моделирование подразделяют на интуитивное и научное. Интуитивное моделирование основывается на представлении, не поддающемся формализации (не обосновывающемся с позиций формальной логики) или не нуждающемся в ней. Примером интуитивной модели можно считать жизненный опыт любого человека или умения и знания, накопленные многовековым опытом человечества и передающиеся от поколения к поколению.

Научное моделирование построено на основании наблюдений за объектом моделирования, логически обосновано и использует минимальное число предположений, принятых в качестве гипотез. Главное отличие научного моделирования от интуитивного заключается в знании внутренних механизмов самого процесса (в то время как интуитивное моделирование ограничено умением выполнять необходимые операции и действия).

Знаковым называют моделирование, использующее в качестве моделей знаковые преобразования какого-либо вида: схемы, графики, чертежи, формулы, наборы символов, включающие также совокупность законов и правил, по которым можно оперировать с выбранными знаковыми объектами [4].

Таким образом, мы подошли к понятию «математическое моделирование».

Математическое моделирование – это идеальное научное знаковое формальное моделирование, при котором описание объекта осуществляется на языке математики, а исследование модели проводится с использованием тех или иных математических методов. Основная задача математического моделирования – выделение законов в природе, обществе и технике и запись их на языке математики.

Рассмотрим некоторые подходы к построению простейших математических моделей, иллюстрирующие применение фундаментальных законов природы. Наиболее распространенный метод построения моделей состоит в применении фундаментальных законов природы к конкретной ситуации. Эти законы общепризнанны, многократно подтверждены опытом, служат основой множества научно-технических достижений. Поэтому их обоснованность не вызывает сомнений, что, помимо всего прочего, обеспечивает исследователю мощную психологическую поддержку.

а) Сохранение энергии. Этот закон известен почти двести лет и занимает, пожалуй, наиболее почетное место среди великих законов природы. Полагаясь на него, эксперт по баллистике, желающий быстро определить скорость револьверной пули и не имеющий поблизости специальной лаборатории, может воспользоваться относительно простым устройством типа маятника – груза, подвешенного на легком жестком и свободно вращающемся стержне (Рис. 4)

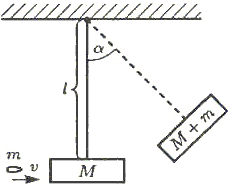
Рис. 4

Пуля, застрявшая в грузе, сообщит системе "пуля – груз" свою кинетическую энергию, которая в момент наибольшего отклонения стержня от вертикали полностью перейдет в потенциальную энергию системы. Это описывается цепочкой равенств

Здесь кинетическая энергия пули массы m, имеющей скорость v, M – масса груза, V – скорость системы "пуля–груз" сразу после столкновения, g – ускорение свободного падения, l – длина стержня, α – угол наибольшего отклонения. Искомая скорость определяется формулой , которая будет вполне точной, если не учитываемые нами потери энергии на разогрев пули и груза, на преодоление сопротивления воздуха, разгон стержня и т. д., невелики. Это, на первый взгляд, разумное рассуждение на самом деле неверно. Процессы, происходящие при "слипании" пули и маятника, уже не являются чисто механическими. Поэтому примененный для вычисления величины V закон сохранения механической энергии несправедлив: сохраняется полная, а не механическая энергия системы. Он дает лишь нижнюю границу для оценки скорости пули (для правильного решения этой простой задачи надо воспользоваться также законом сохранения импульса).

б) Сохранение материи. Именно этим соображением руководствуется школьник, решающий задачу о заполнении бассейна водой, втекающей и вытекающей из двух труб. Конечно же, область применения этого закона несравненно шире.

Пусть, например, имеется небольшое количество радиоактивного вещества (урана), окруженного толстым слоем "обычного" материала (свинца), — ситуация типичная либо при хранении делящихся материалов, либо при их использовании в энергетике (Рис. 5).

Рис. 5

Под словом "небольшой" подразумевается упрощающее обстоятельство, а именно то, что все продукты распада, не испытывая столкновений с атомами вещества, беспрепятственно покидают область I. Другими словами, длина свободного пробега продуктов распада в первом веществе значительно больше характерных размеров самого материала L_I, Т.е. . Слова "толстый слой" означают, что в согласии с целями хранения продукты деления полностью поглощаются в области II. Это гарантируется при выполнении противоположного условия , где – длина пробега продуктов распада во втором веществе, L_II – его характерный размер.

Итак, все, что вылетает из области I, поглощается в области II, и суммарная масса обоих веществ со временем не меняется. Это и есть закон сохранения материи, примененный к данной ситуации. Если в начальный момент времени t=0 массы веществ были равны M_I(0) и MII(0), то в любой момент времени справедлив баланс

M_I(0) + M_II(0)= M_I(t) + M_II(t) (3)

Одного уравнения (3), очевидно, недостаточно для определения текущих значений двух масс – M_I(t) и M_II(t). Для замыкания математической формулировки необходимо привлечь дополнительное соображение о характере распада. Оно гласит, что скорость распада (число атомов, распадающихся в единицу времени) пропорционально общему числу атомов радиоактивного вещества. За небольшое время dt между моментами t и t + dt всего распадется

атомов.

Здесь вторично использован закон сохранения вещества, но, применительно не ко всему процессу, а к отрезку времени dt. В этом уравнении, описывающем баланс атомов, в правой части стоит знак минус (вещество убывает), а величина отвечает некоторому среднему значению числа атомов за рассматриваемое время. Перепишем его в дифференциальной форме:

.

Учитывая, что где – атомный вес вещества I, получаем

(4)

При самопроизвольной радиоактивности любой атом имеет некоторую, не зависящую от состояния окружающего вещества, вероятность распада. Поэтому чем больше (меньше) самого радиоактивного вещества, тем больше (меньше) выделяется продуктов распада в единицу времени. Коэффициент пропорциональности (постоянная распада) определяется конкретным веществом. Уравнения (3), (4) вместе составляют математическую модель рассматриваемого объекта.

Интегрируя (4), получаем, что масса делящегося материала убывает по экспоненциальному закону и при в области I вещество полностью исчезает.

Так как суммарная масса в соответствии с (3) остается постоянной, то в области II количество вещества растет:

и при продукты распада полностью переходят из области I в область II [4] .

Мы рассмотрели лишь некоторые подходы к построению простейших математических моделей

Приведем несколько определений понятия «математическая модель».

1) Математическая модель – приближённое описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики [15].

2) Математическая модель некоторого объекта, процесса или явления – запись его свойств на формальном языке с целью получения нового знания (свойства или свойств) об изученном процессе путем применения формальных методов.

3) Математическая модель – формализованное описание системы (или операции) на некотором абстрактном языке, например, в виде совокупности математических соотношений или схемы алгоритма, т. е. такое математическое описание, которое обеспечивает имитацию работы систем или устройств на уровне, достаточно близком к их реальному поведению, получаемому при натурных испытаниях систем или устройств [3].

К математическим моделям предъявляются следующие основные требования:

- универсальность – характеризует полноту отражения в ней свойств реального объекта. Математическая модель отражает не все, а лишь некоторые существенные свойства реального объекта;

- точность – оценивается степенью совпадения значений выходных параметров реального объекта и значений тех же параметров, рассчитанных с помощью модели;

- экономичность – характеризуется затратами вычислительных ресурсов на ее реализацию.

- адекватность – достаточно точное отображение свойств объекта, т.е. способность отражать заданные свойства объекта с погрешностью, не выше заданной.

К математическим моделям предъявляется и целый ряд других требований, среди которых следует выделить следующие:

гибкость – возможность воспроизведения различных ситуаций во всем диапазоне изменения условий и параметров;

модульность, т.е. соответствие конструкций модели структурным составляющим объекта (системы);

алгоритмизируемость, т.е. возможность разработки соответствующих алгоритмов и программ, реализующих математическую модель на ЭВМ;

наглядность, т.е. удобное визуальное восприятие модели.

Математическое моделирование и связанный с ним компьютерный эксперимент незаменимы в тех случаях, когда натурный эксперимент невозможен или затруднен по тем или иным причинам. Например, нельзя поставить натурный эксперимент в истории, чтобы проверить, «что было бы, если бы...» Невозможно проверить правильность той или иной космологической теории. В принципе возможно, но вряд ли разумно, поставить эксперимент по распространению какой-либо болезни, например чумы, или осуществить ядерный взрыв, чтобы изучить его последствия. Однако все это вполне можно сделать на компьютере, построив предварительно математические модели изучаемых явлений.

Альтернативой формальному (математическому) подходу является экспериментальный подход. К его недостаткам можно отнести, например, высокую стоимость подготовки и проведения экспериментов, а также получение частного знания (знания о конкретном объекте исследования, а не о классе объектов).

Например, пусть требуется определить воздействие х на некоторый процесс или объект, при котором его результирующая характеристика у имеет максимально возможное значение (Рис. 6).

(а) (б)

Рис. 6

На рисунке 6(а) показан эмпирический (экспериментальный) подход к решению поставленной задачи, который состоит в экспериментальном определении значения параметра у для нескольких значений входного воздействия х. Среди них найдено наибольшее, и оно принимается за максимум. Как видим из этого рисунка, возможно несколько значений воздействия х (х₄ и х₅), при которых у имеет наибольшее значение, но ни одно из них не является настоящим максимумом, который, возможно, лежит между ними.

Математический подход (Рис. 6(б)) предполагает наличие математической модели процесса типа y = f(x). Взяв производную и приравняв ее к нулю, получим уравнение, решением которого является точное значение x_max , доставляющее максимум функции у.

Для оценки значимости совпадения или несовпадения модельных и экспериментальных результатов широко используются методы математической статистики. Вместе с тем не следует переоценивать результаты такой проверки. Хорошее совпадение модельных и экспериментальных данных, вообще говоря, не доказывает точности модели, а лишь подтверждают ее функциональную пригодность для моделирования. Всегда может быть предложена модель, обеспечивающая лучшее совпадение с экспериментом, но не лучшее описание моделируемого объекта или процесса.

Математическое моделирование позволяет до создания реальной системы (объекта) или возникновения реальной ситуации рассмотреть возможные режимы работы, выбрать оптимальные управляющие воздействия, составить объективный прогноз будущих состояний системы.

Математическая модель, основанная на некотором упрощении, никогда не бывает тождественна рассматриваемому объекту, не передаёт всех его свойств и особенностей, а является его приближённым отражением. Однако в результате замены реального объекта соответствующей ему моделью появляется возможность математически сформулировать задачу его изучения и воспользоваться для анализа его свойств математическим аппаратом, который не зависит от конкретной природы данного объекта. Этот аппарат позволяет единообразно описать широкий круг фактов и наблюдений, провести их детальный количественный анализ, предсказать, как поведёт себя объект в различных условиях, т.е. прогнозировать результаты будущих наблюдений.